钢管混凝土中核心混凝土的徐变系数终值研究
2012-08-16李永进廖飞宇
李永进,廖飞宇
(福建农林大学交通学院,福建福州350002)
在长期荷载作用下,钢管混凝土中的核心混凝土会产生徐变和收缩,使得结构出现内力重分布,应力集中等问题,严重者将导致结构破坏。因此,钢管混凝土结构在长期荷载作用下的力学性能越来越引起人们的重视[1-12]。
对混凝土的徐变性能进行研究,首先要选用合理的徐变系数表达式,即建立起徐变变形与加载龄期及持荷时间之间的数学关系(反映徐变随时间变化规律)。有了徐变系数表达式,任意加载龄期t0在任意时刻t的混凝土徐变系数就可以求得,采用合适的徐变计算理论和方法就可以对结构的徐变特性进行分析。徐变系数的计算表达式多写成由时间系数乘以徐变系数终值的形式。时间系数有对数函数、幂函数、指数函数、双曲线函数等不同表达形式,如ACI209[13]公式和CEB-FIP[14]规范公式;徐变系数终值是混凝土最终的徐变变形值,反映了混凝土的徐变程度,是进行结构徐变分析的基础。
而对于钢管混凝土中的核心混凝土,因钢管的存在而与大气环境隔绝且其徐变变形受到钢管的限制,故钢管中核心混凝土的徐变系数终值要明显不同于普通混凝土。因此,要研究长期荷载作用下钢管混凝土的力学性能,首先要明确钢管中核心混凝土的徐变系数终值。通过试验研究发现[2-8],长期荷载作用下钢管混凝土中核心混凝土的徐变系数终值要远小于普通混凝土结构的徐变系数终值;按ACI209[13]、日本路桥规范JSHB、CEB-FIP[14]等混凝土收缩徐变模型计算的徐变系数终值不适用于钢管混凝土的中核心混凝土。虽然,国内外研究者对钢管混凝土在长期荷载作用下的力学性能已经进行了较多的试验研究与理论分析[2-12],但尚未见到有关长期荷载作用下钢管混凝土中核心混凝土徐变系数终值定义的明确方法。
本文基于合理的材料本构关系模型,采用有限元法对在长期荷载作用下钢管混凝土柱的变形-时间关系曲线进行了计算。有限元模型得到了试验结果的验证。在此基础上,对长期荷载作用下钢管混凝土中核心混凝土徐变系数终值的取值方法进行了分析和探讨,提出了钢管混凝土徐变系数终值的计算方法,结果可为进一步研究钢管混凝土在长期荷载作用下的工作机理以及相关工程实践提供参考。
1 有限元分析模型
基于ABAQUS有限元分析平台,采用有限元法建立长期荷载作用下钢管混凝土柱力学性能分析模型,对长期荷载作用阶段钢管混凝土的变形-时间关系曲线进行计算。
1)钢材采用ABAQUS软件中提供等向弹塑性模型[15],满足Von Mises屈服准则。
2)混凝土采用文[12]提出的考虑时间效应的三维粘弹性本构模型来模拟核心混凝土在长期荷载作用下的力学性能。该模型中混凝土的徐变系数采用指数函数形式,如式(1)所示。

式中:φ(t)为t时刻的徐变系数;φu为徐变系数终值;指数幂k是影响混凝土变形趋势的相关材料参数,k=0.02。
关于三维粘弹性本构模型的应力-应变关系,其表达式如下:

式中:σ为应力;ε为应变;t是持荷时间;t0代表加载龄期;δij为Kronecker符号(当i=j时,δij=1;当i≠j时,δij=0),λ和G为材料参数;ψ1(t)和 ψ2(t)分别为相应体应变εkk(t)和剪应变εij(t)的松弛函数。λ,G,ψ1(t)和ψ2(t)的表达式如下所示:

式中:E(t0)和G(t0)分别为施加长期荷载时,混凝土的弹性模量和剪切模量;h=(1+φu)k。
采用ABAQUS有限元平台,建立了长期荷载作用下钢管混凝土柱的有限元分析模型。钢管采用四节点壳单元(S4R),混凝土采用八节点三维实体单元(C3D8R),钢管和混凝土间的界面模型采用界面法线方向的硬接触和切线方向的库仑摩擦模型[15]。为了提高计算效率,根据荷载及几何模型的对称性,取构件的1/4模型进行分析。单元网格划分和边界条件如图1(以圆钢管混凝土柱为例)所示。采用力加载的方式对钢管混凝土柱施加长期荷载值NL,并保持NL不变,直至长期荷载作用结束;便可获得长期荷载作用下构件的变形-时间关系曲线。
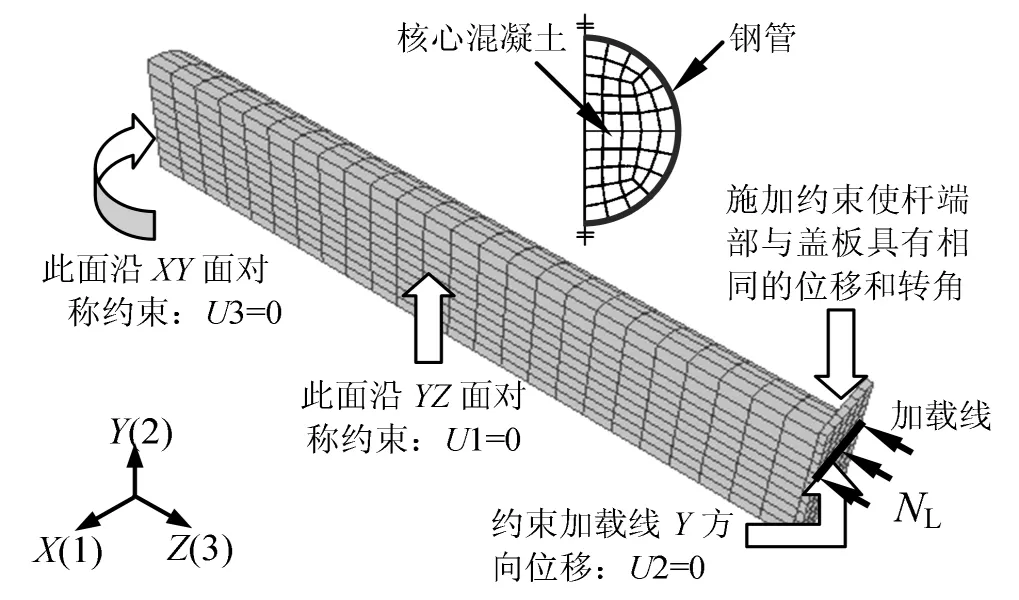
图1 有限元模型示意图Fig.1 Finite element model of CFST column
2 有限元模型验证
为了验证理论模型的正确性,利用上述有限元模型,对收集到的钢管混凝土轴压试件在长期荷载作用下的变形试验结果进行了计算。包括10个圆钢管混凝土和12个方钢管混凝土试件在长期荷载作用下的变形试验数据。试件的具体参数如表1所示。表中,D(B)为钢管的外直径(外边长),ts为钢管的厚度,L为试件的长度,fy为钢管的屈服强度,fck为混凝土抗压强度标准值,NL为施加在构件上的长期荷载,α(=As/Ac,其中,As为钢管的截面积;Ac为混凝土截面积)为钢管混凝土的截面含钢率[1],ξ(=α×fy/fck)定义为约束效应系数[1]。
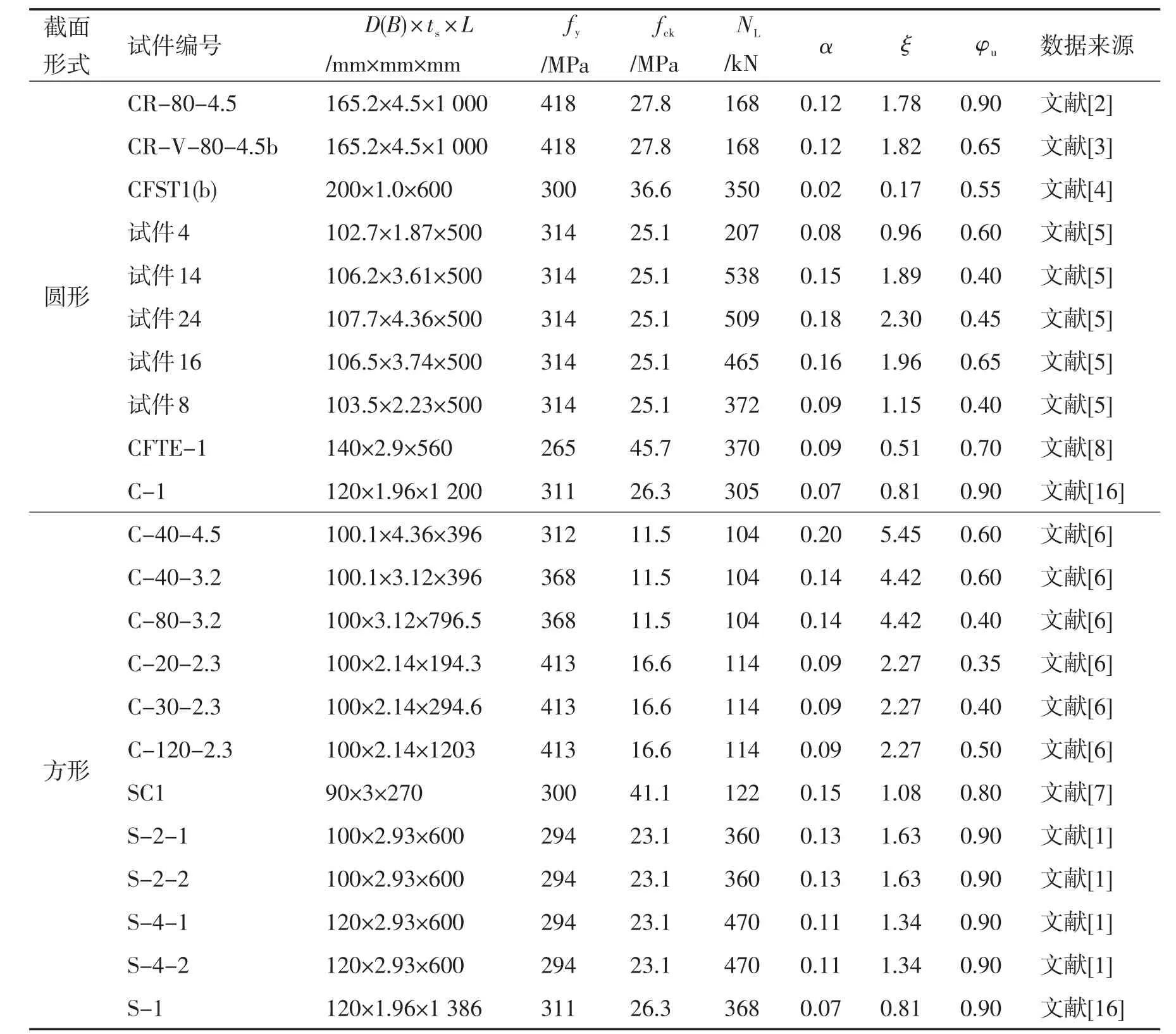
表1 钢管混凝土轴压试件一览表Tab.1 Details of CFST column specimens
限于篇幅,图2仅给出了部分钢管混凝土轴压试件在长期荷载作用下的变形曲线的计算结果与实测结果的比较图。可见计算结果与试验结果吻合较好。
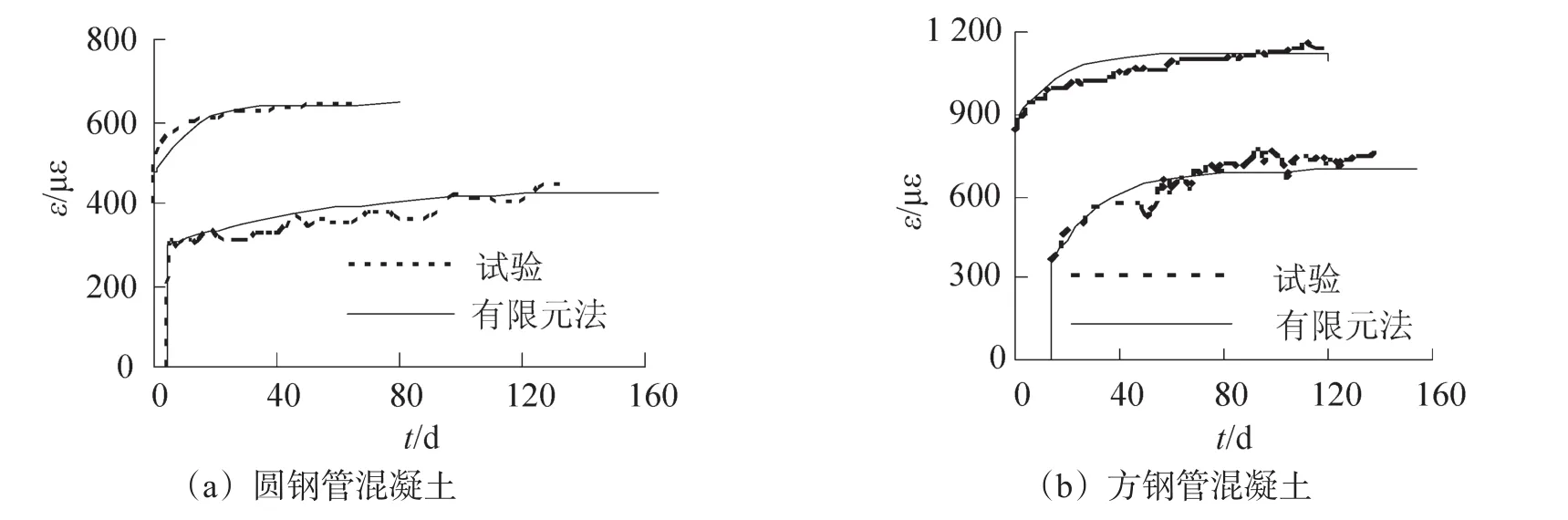
图2 计算曲线与实测变形曲线的对比(轴压试件)Fig.2 Comparisons between predicted deformation curves and experimental results(column specimens)
表2所示为收集到的在长期荷载作用下钢管混凝土偏压试件的算例情况,包括4个圆钢管混凝土和2个方钢管混凝土。
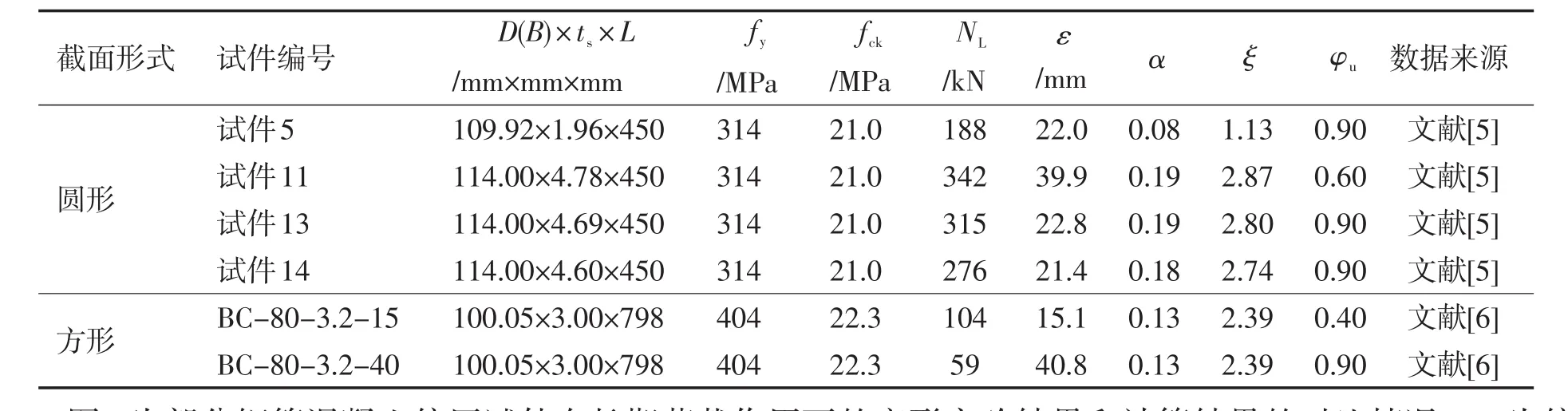
表2 钢管混凝土偏压试件一览表Tab.2 Details of CFST beam-column specimens
图3为部分钢管混凝土偏压试件在长期荷载作用下的变形实验结果和计算结果的对比情况,εL为偏压试件截面上产生的平均应变。可见计算结果与试验结果基本吻合。

图3 计算曲线与实测变形曲线的对比(偏压试件)Fig.3 Comparisons between predicted deformation curves and experimental results(beam-column specimens)
3 徐变系数终值分析
通过对收集到的长期荷载作用下钢管混凝土变形-时间关系试验曲线的拟合,可以得到钢管中核心混凝土的徐变系数终值φu,结果列于表1和表2中。
从表1可见,对于轴压试件,当含钢率 α[1]在0.02~0.20范围内,约束效应系数 ξ[1]在0.17~2.30(圆钢管混凝土)或0.81~5.45(方钢管混凝土)范围内,核心混凝土的徐变系数终值φu都在0.4~0.9之间变化。对于表2中的钢管混凝土偏压试件,与轴压试件类似,其徐变系数终值φu的上限值也为0.9。
采用ACI209[13]和CEB-FIP[14]提供的混凝土徐变模型分别对钢管混凝土中核心混凝土的徐变系数终值φcon进行计算,并与上文由试验拟合得出的核心混凝土的徐变系数终值φu进行比较,对比结果如图4所示。
可见,在长期荷载作用下,由于外包钢管的存在,影响了核心混凝土的徐变,在一定程度上降低了核心混凝土的徐变程度(即徐变系数终值φu)。钢管混凝土中核心混凝土的徐变系数终值φu都明显小于分别按ACI209[13]和CEB-FIP[14]计算的徐变系数终值 φcon,φu仅为按ACI209[13]计算 φcon的24%~68%,φu仅为按CEB-FIP[14]计算 φu的22%~59%。由此可见,采用现有普通混凝土模型如ACI209[13]和CEB-FIP[14]计算钢管混凝土中核心混凝土的徐变系数终值均不合理,有必要重新确定钢管中核心混凝土的徐变系数终值。
而由对试验曲线拟合的结果可得,无论圆钢管混凝土,还是方钢管混凝土,在长期荷载作用下钢管混凝土中核心混凝土的徐变系数终值φu其上限值为0.9左右,因此,本文建议,在钢管屈服强度 fy=235~420 MPa、C20-C60混凝土、α =0.02~0.2、ξ=0.1~5、偏心率 ε/r=0~1.0、长细比 λ=10~40、轴压比 n=0.1~0.6参数范围,采用φu=0.9作为钢管混凝土中核心混凝土的徐变系数终值是合理且偏于安全的。
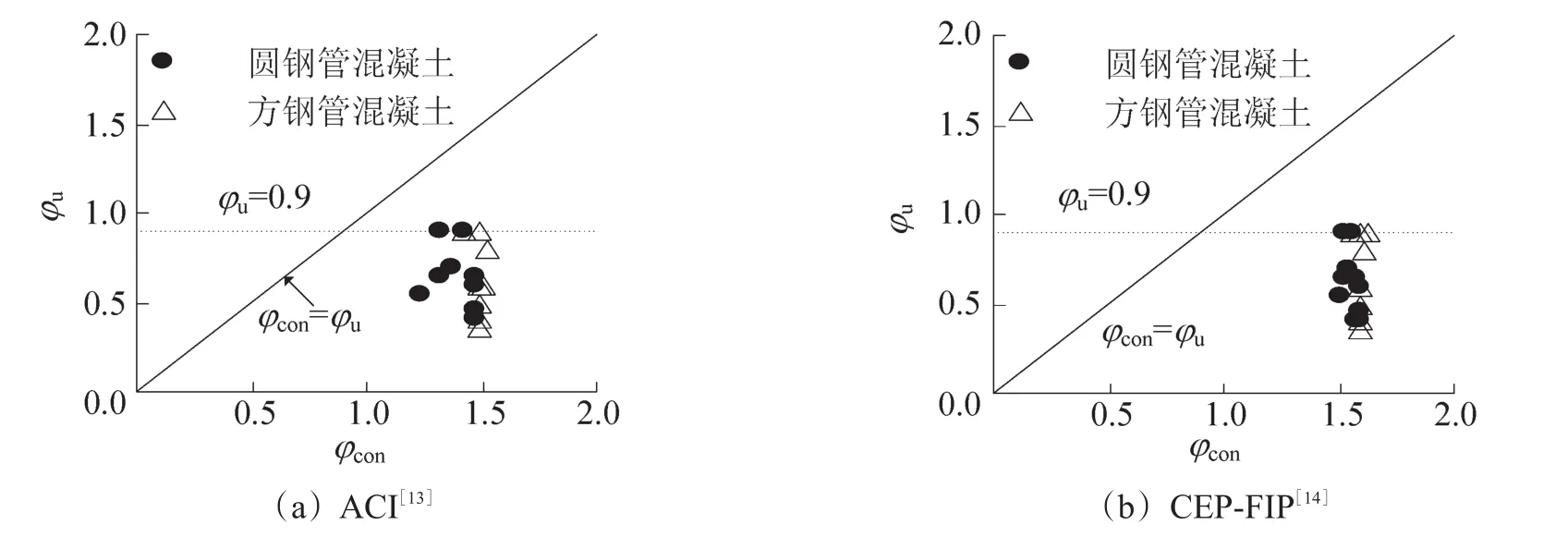
图4 徐变系数终值的对比Fig.4 Comparisons of ultimate creep coefficients
4 结论
1)采用的有限元法可较好地用于模拟长期荷载作用下钢管混凝土柱的力学性能,计算结果得到试验结果的验证,可为以后进一步研究钢管混凝土柱在长期荷载作用下的工作机理提供分析模型。
2)在长期荷载作用下,由于外包钢管的存在,钢管混凝土中核心混凝土的徐变系数终值要明显小于分别按ACI209[13]和CEB-FIP[14]计算的徐变系数终值。
3)在长期荷载作用下,钢管混凝土中核心混凝土的徐变系数终值φu的上限值为0.9。从安全的角度考虑,采用φu=0.9作为核心混凝土的徐变系数终值。
[1]韩林海.钢管混凝土结构-理论与实践[M].北京:科学出版社,2007:404-440.
[2]NAKAI H,KURITAA,ICHINOSE L H.An experimental study on creep of concrete filled steel pipes[C]//Proc of 3rd Inter Confer on Steel and Concrete Composite Structures,Japan:Fukuoka,1991:55-60.
[3] ICHINOSE L H,WATANABE E,NAKAI H.An experimental study on creep of concrete filled steel pipes[J].Journal of Constructional Steel Research,2001,57(4):453-466.
[4]TERREY P J,BRADFORD M A,GILBERT R I.Creep and shrinkage of concrete in concrete-filled circular steel tubes[C]//Proc of 6th Inter Symposium on Tubular Structures,Australia:Melbourne,1994:293-298.
[5]谭素杰,齐加连.长期荷载对钢管混凝土受压构件强度影响的试验研究[J].哈尔滨建筑工程学院学报,1987,20(2):10-24.
[6]MORINO S,KSWANGUCHI J,CAO Z S.Creep behavior of concrete filled steel tubular members[C]//Proc of an Engineering Foundation Confer on Steel-Concrete Composite Structure.ASCE:Irsee,1996:514-525.
[7] UY B.Static long-term effects in short concrete-filled steel box columns under sustained loading[J].ACI Structural Journal,2001,98(1):96-104.
[8]KWON S H,KIM Y Y,KIM J K.Long-term behaviour under axial service loads of circular columns made from concrete filled steel tubes[J].Magazine of Concrete Research,2005,57(2):87-99.
[9]韩林海,陶忠,刘威,等.长期荷载作用下方钢管混凝土轴心受压柱的变形特性[J].中国公路学报,2001,14(2):52-57.
[10]韩林海,刘威.长期荷载作用对圆钢管混凝土压弯构件力学性能影响的研究[J].土木工程学报,2002,35(2):8-19.
[11]WANG YUYIN,GENG YUE,RANZI G,et al.Time-dependent behaviour of expansive concrete-filled steel tubular col-umns[J].Journal of Constructional Steel Research,2011,67(3):471-483.
[12]李永进.考虑长期荷载作用影响时钢管混凝土柱的力学性能研究[D].福州:福州大学,2009:42-70.
[13] ACI COMMITTEE.Prediction of creep shrinkage and temperature effects in concrete structures[S].Farmington Hills,Mich,USA:American Concrete Institute,1992.
[14]CEB-FIP.CEB-FIP model code 1990[S].Londm:Thomas Telford Ltd,1990:437-446.
[15]黄宏.圆中空夹层钢管混凝土内管径厚比限值探讨[J].华东交通大学学报,2011,28(3):31-34.
[16] HAN LINHAI,LI YONGJIN,LIAO FEIYU.Concrete-filled double skin steel tubular(CFDST)columns subjected to long-term sustained loading[J].ThinWalled Structures,2011,49(12):1534-1543.
