校正力对V形件弯曲回弹的影响

李 莹，周 睿

（山东大学 工程训练中心，山东 济南 250002）

1 引言

冲压件在成形过程中不但存在塑性变形，还存在弹性变形，卸载后由于弹性变形的恢复，即产生回弹现象[1]。成形后的回弹量影响着冲压件的最终形状，当回弹量超过允许范围，就成为成形缺陷。回弹问题的存在会影响冲压件的形状尺寸精度和表面质量，以及后续的装配等工序和焊装件的使用可靠性。因此精确的计算给定冲压件的回弹量大小及分布就显得尤为重要。

对于回弹常见的研究方法有解析研究、实验研究和有限元数值模拟研究。

Hill提出了平面应变条件下弹塑性弯曲的基本理论，推导了纯弯曲条件下不考虑材料硬化的完全解，并指出中性层在弯曲过程中会发生移动[2]。F.Pourboghrat提出了一种半解析法，用于预测平面应变条件下薄板成形的回弹问题[3]。Daw-Kwei Leu提出了一种考虑板料厚向异性系数r、硬化指数n的薄板纯弯曲力学模型，用于评价回弹、弯曲性和最大弯矩[4]。Thomson通过一系列试验研究了一般钢板、镀锌钢板和镀铝锌钢板U型件的回弹及侧壁扭曲情况，讨论了工艺参数对回弹的影响[5]。Livatyali研究了几何和工艺参数对直翻边回弹的影响，并采用局部加压校正来消除直翻边的回弹[6]。Tan提出了一种控制V型压弯件回弹的经验模型，试验利用凸模的过量位移产生V型件的过量弯曲借以补偿回弹[7]。You-Min Huang利用有限元模拟方法，研究了冲压工艺参数：如摩擦系数、凹模圆角半径、凹凸模间隙等对 U形件卸载后最终形状的影响[8]。赵国伟以典型的弧形弯曲件为研究对象，并运用有限元分析软件ANSYS/LS-DYNA对不同材料、板厚、摩擦系数等因素对回弹的影响进行了分析和比较[9]。

V形件是一种典型的冲压件，许多复杂零件的弯曲回弹问题都可以通过V形件的回弹来解释，所以研究V形件的回弹在冲压件回弹问题中具有很强的代表性。影响V形件回弹的因素有很多，如弯曲校正力、弯曲角、相对弯曲半径、材料性能等，其中校正力是最重要的影响因素之一。

目前，不论是国内还是国外，虽然在研究校正弯曲力对回弹的影响方面做了大量的研究工作，但主要是通过经验数值和简单的计算来确定。其中校正力的经验公式比较常用[10]：

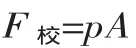
式中：F校——校正弯曲力；

A——校正面垂直投影面积；

p——单位面积上的校正力，可查询有关手册。

但是，由于回弹涉及的因素较多，较为复杂，并且具体到每一个不同的冲压条件，目前还没有一个精确的计算公式能够保证所有回弹量在误差允许的范围内。考虑到校正力对于控制回弹有重要的作用，用计算机数值模拟技术来研究校正力对回弹值的影响，另外通过实验法来验证数值模拟过程的可行性。为预测回弹量设计模具提供另一种思路。本文将采用数值模拟与实验相结合的方法，研究校正力对V形件弯曲回弹的影响规律。

2 板料弯曲成形过程和回弹分析

2.1 V型件弯曲时的回弹

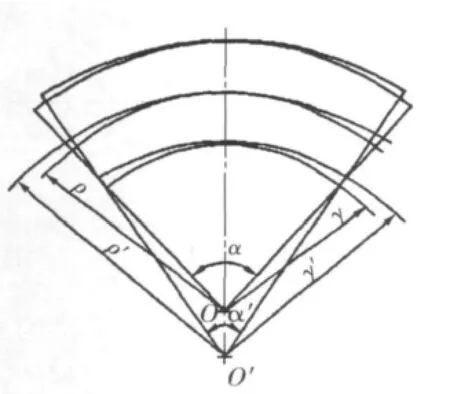
图1 弯曲件回弹前后的几何尺寸

板料的回弹，表现为弯曲件曲率变化和弯曲角的变化。如图1所示，ρ、α、γ 分别表示回弹前板料中性层的曲率半径、弯角和弯曲板料内表面的圆角半径；ρ′、α′、γ′分别表示卸载后板料中性层的曲率半径、弯角和弯曲板料内表面的圆角半径[11]。这里定义，Δα为回弹角，那么

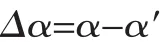
ΔK表示曲率的减少量，则

为简单起见，本文仅讨论校正力对角度回弹（即Δα）的影响。

2.2 弯曲变形过程

板料的弯曲可分为自由弯曲过程和校正弯曲过程[12]。自由弯曲时，由于弯曲件的成形部分在冲压过程中不受模具的校正影响，所以卸载后回弹量较大。而校正弯曲是在板材自由弯曲的终了阶段，凸模继续下行将弯曲件压靠在凹模上，对弯曲件的圆角和直边进行精压，减少了回弹的影响。

自由弯曲和校正弯曲的回弹趋势也有很大的差异。如图2所示，自由弯曲过程，把弯曲件的一半分成三段：圆角区OA段、直边变形区AB和直边不变形区BC段。OA与AB直至变形终了始终产生内闭的弯曲变形（弯曲角与弯曲半径均减小）。所以，回弹的趋势均为外开。如图2b。可见，用无底凹模弯曲V形件时回弹量是比较大的。

图2 用无底凹模弯曲V形件

如果用带底的凹模弯曲V形件，如图3所示，回弹情况有很大的不同。当变形到图3a位置Ⅰ的状态时，相当于图2位置Ⅱ，但凹模支撑点却沿斜面下滑了。

图3 用带底凹模弯曲V形件

随着凸模继续下压，凹模支撑点将继续下滑，支撑点以外的板料将开始朝反方向弯曲，如位置Ⅱ所示。这时弯曲件直边变形区AC段呈S形，切点A与B将变形部分板料分成三段弧形：OA段、AB段和BC段。从位置Ⅱ开始，凸模继续下压，OA段与BC段将产生内闭的弯曲，而AB段则产生外开的弯曲，图3a位置Ⅲ显示了这种变形趋势，直到完全贴膜。当弯曲件脱离模具后，OA段与BC段将产生外开回弹，而AB段则产生内闭回弹，如图3b所示。这三段综合作用的结果将决定弯曲件回弹后的形状。如果OA段与BC段外开回弹量之和大于AB段内闭回弹量，弯曲件将产生正回弹。相反，则产生负回弹。

3 V形件弯曲回弹数值模拟

3.1 有限元模型的建立

图4 V形件弯曲的三维模型

图5 有限元模型

以济钢集团生产的08F钢为研究材料，进行三维曲面造型，包括：凸模、凹模、毛坯（无压边成形）。板料的尺寸：长×宽×厚=120mm×45mm×1mm；凸模圆角半径为4mm，弯曲角度为90°；凹模圆角半径5mm，凹模开口尺寸90mm。如图4所示。

建立有限元模型如图5所示，采用DYNAIN的方法，进行成形及回弹的模拟。相关参数如下：

坯料厚度1.0mm，力学性能参数如表1所示，模具采用刚体材料模型，坯料采用自适应技术，采用第36号即3参数BARLAT材料模型。坯料与凹模、凸模之间的摩擦系数都是0.125。

表1 材料力学性能

3.2 校正力对回弹的影响

将成形模拟后得到的DYNAIN文件，导入到DYNAFORM进行回弹模拟，利用DYNAFORM的后处理工具，可以得到z方向的回弹量。但是，如图6所示，对于任一截面来说，由于板料在成形之前三点受力的影响导致最终卸载后直边部分发生变形，即直边的不同位置的回弹量不同；不同截面同一位置回弹量不同（如图7、8所示）。所以为了提高测量精度，选取多个截面（本例选5组）进行测量，然后把得到的回弹结果取平均值，得到近似的测量结果。

图6 板料三点受力成形过程

图7 直边部分角度测量

图8 不同截面同一位置回弹量值

为了便于分析不同校正力对回弹的影响，选取多组不同校正力来进行研究，得到的回弹量与校正力的关系如表2和关系曲线如图9所示。

表2 校正力与回弹值对应关系

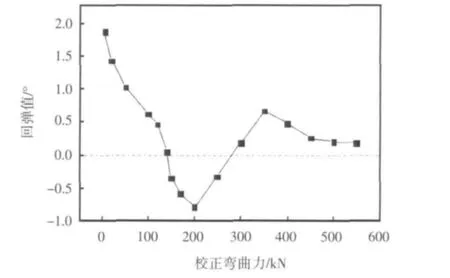
图9 校正力与回弹值的模拟关系曲线

分析校正力-回弹曲线，在作用力较小的时候，回弹值较大，随着力的增加,回弹逐渐减小,在150kN左右回弹值接近于零。随后，随着力的增加，开始出现负回弹，在200kN时负回弹最大。此后，作用力增加，负回弹减小，在280kN时回弹值再次接近于零。最后，回弹值在经过350kN时达到了一个极大值，达到极大值后，回弹又逐渐减小，并趋于恒定。

在较小的力的作用下进行校正，因为自由弯曲过程的回弹较大，所以校正力并不能很好的对直边部分进行精压，导致回弹量大。而校正力增加之后，板料受到凸模强烈的镦压，产生很大的压应力。增加了变形区的塑性变形，也改变了切向应力的分布，切向压应力数值增大，拉应力减小，并使切向受压的内区向受拉的外区扩展。这样，卸载后，受压的内区与受拉的外区的回弹抵消，使回弹减小。

出现负回弹是因为当r/t很小时，进行校正弯曲（参考图3），OA段的回弹量很小，几乎为零。这时，AB段的向内的回弹量可能超过BC段的外开回弹，使整体产生负回弹。如果校正力继续增加，使得rp区板料减薄，这样AB段的向内回弹将受到限制，使得BC段的外开回弹超过AB段向内回弹，所以也就再次出现了正回弹。最终即使校正力继续增大，板料的变薄程度有限，当板厚减薄约2%～5%时，回弹值就比较稳定了。

在工程中，往往是通过校正力对回弹进行控制。从经验来讲说，很多情况下都是加大校正力来减小回弹。但是对于简单的V形件来说，根据模拟曲线，板料不但会发生正回弹，在一定条件下甚至会有负回弹，那么中间有一个过程可能回弹值会接近与零。所以，如果能够利用计算机模拟技术来找到这个接近零回弹的校正力，这样对控制回弹就起到了指导性作用。

4 V形件回弹过程实验研究

通过计算机模拟，得到了校正力与回弹量之间的关系，为了能够验证计算机数值模拟用于回弹研究的可行性，下面将通过实验来比较其与计算机数值模拟的理论结果。

图10 V形弯曲模具

4.1 实验方案

选 用 08F，材料厚度1mm，以简单V形件为研究对象，取直角作为弯曲角度。在试验机上进行校正弯曲，以研究校正力对回弹的影响规律。试验模具如图10所示。

4.2 实验数据处理

测量每一个零件的角度值，算出每组实验数据的平均值,即对应不同校正弯曲力的回弹角，如表3所示。

表3 校正力与回弹关系

4.3 实验结果分析

由得到的实验数据绘制校正力与回弹角的关系曲线，并将模拟结果绘于同一坐标中，如图11所示。

由图11可以看出，模拟值与实验结果吻合良好，校正力对回弹的影响较为复杂，在校正力较小的情况下回弹比较严重，增加校正力可以控制回弹，但是，根据曲线来看，校正力增大到一定程度对回弹的控制有限。

5 结论

图11 08F钢厚度1mm模拟与实验对比曲线

通过对V形件弯曲回弹的模拟与实验研究可以看出，校正力对控制回弹有重要的作用。在一定范围内，随着校正力的增加，回弹明显减小，但校正力并不是越大越好。当校正力在某一范围时，会发生负回弹，随着校正力的增加，会再次出现正回弹，但此时回弹值随校正力的变化已不明显。

[1]宋 黎，杨 坚，黄天泽.板料弯曲成形的回弹分析与工程控制综述.锻压技术，1996，（1）：18-22.

[2]R.Hill.The Mathematical Theory of Plasticity Clarendon Press.Oxford，1950.

[3]F.Pourboghrat，K.Chung，O.Richmond.Hybrid membrane/shell method for rapid estimation of springback in anisotropic sheet metals.Journal of Applied Mechanics，1998，65（3）：671-684.

[4]Leu.Simplified approach for evaluating bendability and springback in plastic bending of anisotropic sheet metals.journal of Materials Processing Techlology，1997，66：9-17.

[5]Thomson P F，Kim J K.Springback and side-wall Curl of Galvanized and Galvalume steel sheet.Journal of Mechanical working Technology，1989，19：223-238.

[6]Livatyali H，Altan T.Prediction and elimination of springback in straight flanging using computer aided design methods：Part 1.Experimental investigations.Journal of Materials Processing Technology，2001，117（2）：262-268.

[7]Tan Z，Pesson B，Magnusson.An empiric model for controlling springback in V-die bending of sheet metals.Journal of Materials Processing Technology，1992，34：449-455.

[8]You-Min Huang，Daw-Kwei Leu.An elasto-palstic finite element analysis of sheet metal U-bending process.Journal of Material Processing Technology，1995，48：151-157.

[9]赵国伟.板料成形回弹的数值模拟与影响因素.冲压技术，2005，55：3-4.

[10]李硕本.冲压工艺理论及新技术[M].机械工业出版社，2002.

[11]张鼎承.冲压设计手册[M].北京：机械工业出版社，1999，3.

[12]薛启翔.冲压模具设计制造难点与窍门[M].北京：机械工业出版社，2003-03.