基于螺旋理论的5-UPS/UPU并联机床自由度分析

2012-08-16舒宏庭王红州程洪涛

科技视界 2012年30期

舒宏庭王红州程洪涛

(江西省机械科学研究所江西南昌 330002）

0 前言

并联机构是一种由两个及以上独立运动链连接动平台和定平台，具有2-6 个自由度，且采用并联的驱动方式的机构。与串联机构相比较，并联机构具有精度高、结构紧凑、刚度高、承载能力强等优点。由于并联机构的诸多优点而引起了众多学者展开将并联机构应用于机床的研究。并联机床又称为虚拟轴机床，是一种知识密集型机构，实质上它是现代机器人技术与机床结构技术结合的产物，其原型是并联机器人操作机。与传统机床相比，并联机床具有如下优点： 1）刚度重量比大，2）响应速度快。 3）环境适应性强，便于可重组和模块化设计，且可构成形式多样的布局和自由度组合。 4）技术附加值高。可以说，并联机床被认为是本世纪最具有革命性的机床设计突破，代表了21 世纪机床发展的方向。虽然并联机床得到了众多学者的研究，也获得了丰硕的研究成果，但由于其相比传统的机床而言在机构与控制方面相对要复杂的多，受限于并联机构的应用还不成熟，并联机床在我国还没有成熟的产品进入市场，目前国内外研究的并联机床大都集中在三自由度和六自由度的机型上，而对机床来说要加工复杂的零件最多需要五个自由度就可以完成。所以，六自由度并联机构应用在并联机床上将有一个多余的自由度，这显然是一种不必要的浪费；而三自由度的并联机构为完成复杂的任务就必须借助其他两个自由度的运动，这将使得并联机构的优点大打折扣。因此，研究五自由度的并联机构应用于机床是非常有意义的。燕山大学研究了五自由度的并联机床，但其机构构型（5-UPS/PRPU）中的约束支链采用了移动副连接方式，这将影响机床的性能。作者提出采用五自由度并联机构（5-UPS/UPU）应用于并联机床的构型，并分析其自由度数量与性质，证明本机构适合应用于并联机床。

1 结构设计

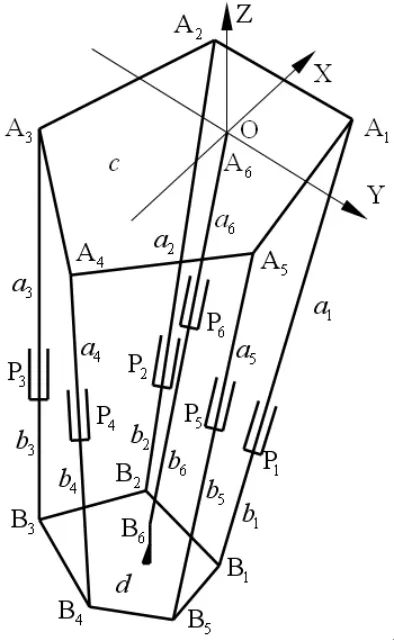
图1

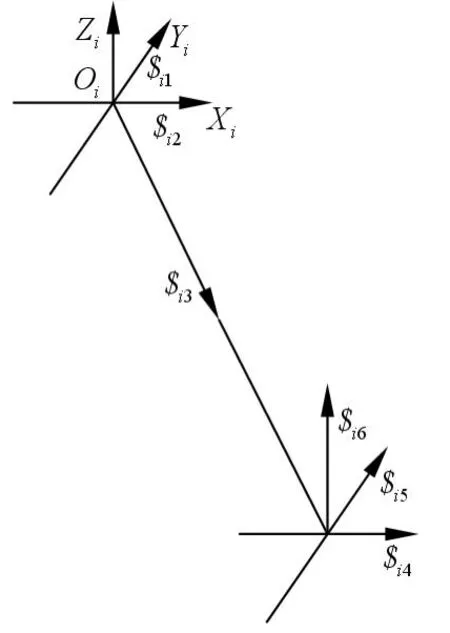
图2

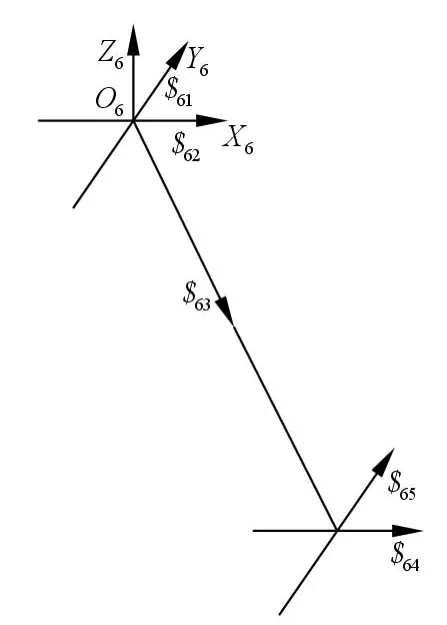
图3

如图1 所示，5-UPS/UPU 机构由静平台c、动平台d 与联接动静平台的六条支链Li（i＝1，2，3，4，5，6）组成，每条支链Li（i＝1，2，3，4，5，6）由杆ai（i＝1，2，3，4，5，6）和杆bi（i＝1，2，3，4，5，6）组成，其中Li（i＝1，2，3，4，5）为主动支链，L6为约束支链，ai（i＝1，2，3，4，5，6）与bi（i＝1，2，3，4，5，6）之间通过移动副pi（i＝1，2，3，4，5，6）联接，主动支链的一端通过虎克铰Ai（i＝1，2，3，4，5）与静平台c 联接，主动支链另一端通过球铰Bi（i＝1，2，3，4，5）与动平台d 联接，约束支链L6分别通过虎克铰A6与虎克铰B6与静平台c与动平台d 联接。虎克铰Ai（i＝1，2，3，4，5）的几何中心为第一正五边形的五个顶点，以第一正五边形的几何中心为坐标原点，垂直于虎克铰Ai（i＝1，2）中心连线的方向为X 轴，平行于虎克铰Ai（i＝1，2）中心连线的方向为Y 轴，第一正五边形所在平面的法向方向为Z 轴建立参考坐标系O-XYZ。