3S系统中地图匹配算法的技术特点探析

2012-08-16刘月

科技视界 2012年30期

刘月

（银川市勘察测绘院宁夏银川 750004）

0 引言

“3S 系统”即GIS/GPS/LBS 系统，就是采取GPS 作为定位手段，为用户提供LBS 服务的嵌入式GIS 系统。 “地图匹配”研究的问题就是如何在3S 系统的导航地图和GPS 信号精度都比较低下的情况下，将接收到的GPS 位置匹配到地图上的实际位置上去。

1 基于地图几何信息的地图匹配算法

1.1 点到点匹配

这种方法简单易行，运行效率高，切合嵌入式软件的实时性要求，但缺点也是显而易见的，具体来讲，主要表现在如下几个方面：

（1）精确度太低，只能匹配到节点，不能匹配到链路或者路段，这是最大的缺点；

（2）跟中间节点的密度有很大关系。很显然，特定链路上的路段划分得越细致，中间节点的数目越多，点到点匹配的精度就越高。

基于以上两个原因，点到点的匹配一般用在匹配起始位置，即匹配第一个GPS 点的时候。具体过程是先找到和第一个GPS 点距离最近的交叉节点，然后将和该交叉节点相连通的所有路段作为备选路段用其它匹配方法进一步匹配后续GPS 点。注意这时点到点的匹配结果也往往是错误的，因为我们不能保证用户刚刚是在位于某个路口的时候开始匹配算法的，但是它起码可以缩小匹配后续GPS 点时的备选路段的范围，并且匹配结果可以很快被后续的匹配算法校正。

1.2 点到线匹配

这是最直观的匹配方法，其实也是现实世界中采用较多的方法。具体步骤是分别计算待匹配的GPS 点向待匹配路段的距离，然后选取距离最短的路段作为匹配结果。这里的待匹配路段既可以选取地图上的所有路段（一般是在匹配无历史历史记录的第一个GPS点的情况下），也可以选取落在GPS 点周围某段距离内的路段。另外需要注意的是，路段是线段而不是直线，点到线段的距离跟点到直线的距离是不同的。如果GPS 点到路段的投影落在路段的延长线上，则一般取GPS 点到路段起点和终点距离的较小值作为点到路段的距离。如图1 所示，P0在路段S0上的投影落在S0上，则P0到S0的距离即为P0到S0的垂直距离；P1 在路段S0上的投影落在S0的延长线上，则P1 到S0的距离就是P1 到S0两端点距离的较小值。

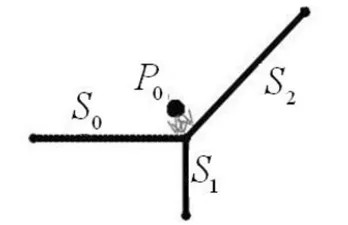
图1 GPS 点到路段的距离

图2 交叉点附近的点到线匹配

图3 近似平行路段中间的点到线匹配

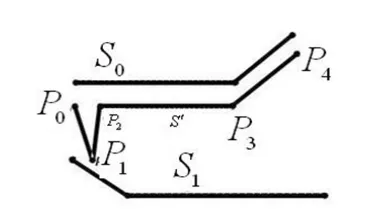
图4 存在异常点情况的线到线匹

点到线匹配实现起来也比较简单，而且在一般情况下的准确度也比较高，但是在以下几种情况下也会很容易发生错误。

（1）在匹配带方向的路段时。通常现实世界中的道路都是双行道，因此在地图上是由两条端点互换方向相反的单向路段表示的。点到线匹配仅考虑了路段的位置，没有考虑路段的方向性，因此是无法区分两条端点互换方向相反的单向路段的。

（2）交叉点附近。交叉点是两条或多条路段交汇的地方，路段的分布比较密集，因此交叉点附近的GPS 点到各路段的距离均比较小，很难利用点到路段的距离将正确的路段筛选出来。如图2 所示，P0到三条路段S0、S1和S2的距离相差无已，很容易将P0匹配到错误的路段。

（3）在两条近似平行的路段中间。在现代城市中，道路的规划有时候会仿照经纬度，构建成一个类似于棋盘状的道路网。在这种类棋盘状道路网中，两条相距不远的同向道路往往是近似平行的。这时候，如果GPS 点在两条道路中间不规则地浮动，则GPS 点也会相应地匹配到距离最近的路段上去。如图3 所示，GPS 点会交替地匹配到S0和S1上，非常不稳定，给用户带来困扰。

尽管存在着以上不足，但由于点到点匹配实现简单，因此在地图精度和GPS 信号精度都比较高，或者移动设备软硬件资源比较紧张以至于不适合采用复杂的地图匹配方法的情况下，仍然经常采用点到线的匹配。

1.3 线到线匹配

线到线匹配是将一系列相邻的两个或多个GPS 点连成一条线段或折线，然后比较该轨迹折线和备选路段或链路的相似度。这里没有考虑折线的方向，只考虑其位置和形状。通常做法是定义出一种计算两条折线之间的距离的方法，然后用两条折线间的距离来衡量它们之间的相似度。

关于两条折线间的距离一种最简单的定义是两条折线上的点的最小距离。即给定两条折线A 和B，在A 上取一点a，在B 上取一点b，使得a、b 之间的距离最小。a、b 之间的距离就表示A 和B 之间的距离。用公式表示为||A-B||min=mina∈A,b∈B||a-b||。

2 基于地图拓扑结构的地图匹配算法

基于地图几何信息的匹配方法的最大缺点是不能保证连续GPS点的匹配路段的连续性，尤其是点到点匹配和点到线匹配，其匹配结果只是一些离散的路段，相互之间没有连接成一条连续折线，这与用户的运动轨迹的连续性不相符合。如果我们想在地图上输出用户的运动轨迹，那么基于地图几何信息的匹配方法往往显得力不从心。另外，基于地图几何信息的匹配方法在选取备选路段时，往往只能选取地图上的所有路段，这在地图数据比较庞大时会极大地影响算法的效率。

针对上述两个缺点，我们可以利用地图的拓扑信息作为补充，保证结果匹配路段的拓扑一致性，并提高匹配的效率。具体方法如下：假设GPS 点Pt匹配到路段S，则将S 以及和S 相连通的路段作为GPS点Pt+1的备选路段。这种方法明显降低了选择备选路段的复杂度，同时提高了匹配结果的准确性。

但是，这种方法也带来一个隐患，即一次匹配错误会导致后续一系列匹配错误。如图4 所示，P0、P1应该分别匹配到S2和S4，但是如果在匹配P0时错误地将其匹配到S1上，则在匹配时，由于备选路段为{S1，S3}，会将P1错误地匹配到S1或S3上去，或者匹配失败。

3 基于统计学和模糊理论的地图匹配算法

与基于地图几何信息和拓扑结构信息的地图匹配算法不同，有一类地图匹配算法开始引入了统计学和模糊理论的方法。这些算法本质上还是基于地图的几何信息和拓扑信息的，只是在运算过程和表现形式上运用了统计学和模糊理论的方法。例如，国外有人提出一种叫做路段约化过滤的算法。每一个原始的GPS 点都被分别投影到附近的路段上，形成一组虚拟的GPS 参考点。显然，正确的匹配结果就是其中某一个GPS 参考点。两个连续的GPS 参考点连接起来形成的矢量线段，与它们相应的两个GPS 参考点连接起来形成的矢量线段，两者的长度和方向应该是近似相等的。基于这一点可以过滤掉不符合条件的参考点组合。

4 综合性的地图匹配算法

现在成熟的地图匹配算法一般都是综合性的，即将多方面的匹配度进行拟合，首先将每一方面的匹配度量化，再乘以某个权重系数，累加起来得到一个总的匹配度值。可以根据实际情况或实际测试结果通过调整权重系数来使计算出来的匹配度值更加精确。

最典型的是利用地图几何信息和拓扑信息的矢量地图匹配算法。矢量地图匹配算法的步骤大致如下：

（1）初始化算法。当匹配第一个GPS 点，或者由于GPS 信号被屏蔽等原因导致前面的匹配失败时，用点到点匹配或点到线匹配的方法匹配该GPS 点。点到点匹配和点到线匹配的目的都是为了选择初始备选路段集，其中点到线匹配是从GPS 点到周围的路段做垂线，垂线长度小于某个阈值的对应路段均作为备选路段；点到点匹配是首先找到和GPS 点距离最近的交叉点，然后将所有和该交叉点相连通的路段作为备选路段。

（2）当接收到新的GPS 点Pt时，将Pt-1和Pt 连接形成一条矢量线段Pt-1Pt。备选路段为当前路段，以及与该路段相连的其它路段。分别计算Pt-1Pt和每条路段的匹配度，然后选择匹配度最高的作为Pt的匹配结果。