考虑桩土滑移的超长桩沉降非线性算法＊

杨明辉，张小威，赵明华

（湖南大学 土木工程学院，湖南 长沙 410082）

对于超长桩目前尚无明确定义，通常指桩长（z＞50m）较长，基桩承载力主要由桩侧阻所提供的桩[1－2]，而随着我国深厚软土区（沿海地区及内陆湖区）高层建筑及大型跨江、跨海桥梁工程的大量兴建，大量桩基工程桩长已远远超出50m的范畴，深度过百m的已不在少数，如苏通长江大桥百m长桩就有410根[3].超长桩基桩承载力非常高，在正常工作荷载下，仅有部分桩侧摩阻力充分发挥，但高层建筑或大型桥梁工程对沉降要求极为严格，沉降量往往成为控制超长桩承载能力的首要指标，因此研究超长桩荷载－沉降关系具有重要的工程意义.

合理地模拟超长桩荷载传递规律是研究超长桩荷载－沉降关系的关键因素.大量研究表明，众多深厚软土区超长桩桩周土层由表面硬壳层、淤泥层、软土层等性质差异巨大的土层组成，在荷载作用下将出现硬化及软化等不同的屈服特性，且在荷载传递过程中，桩与土的变形往往不协调，即出现明显的桩土滑移现象，鉴于上述原因，导致超长桩的传力体系十分复杂，目前工程应用一直采用半经验半理论的方法[4].

针对上述情况，本文在讨论超长桩荷载传递模型的基础上，采用刚度矩阵法对超长桩的沉降进行非线性求解，建立了一种可较全面地考虑桩周土体的成层性及非线性、桩土滑移现象的超长桩沉降计算方法，为工程计算提供参考.

1 超长桩桩土界面模型

目前，对于桩土相对位移与桩侧摩阻力的关系，大都采用佐滕悟（1965）[5]的线弹性－全塑性数学模型.但如前所述，对于深厚软土区的土体相互工程性质差异较大，在竖向荷载作用下，将出现应变软化或应变硬化类型土体，采用线弹性－全塑性数学模型无法准确地描述其特性，因此本文采用三折线进行模拟，桩侧摩阻力与桩土相对位移关系如图1（a）和（b）所示.

图1 不同类型土体的侧阻传递曲线Fig.1 Shaft resistance transfer model for different soils

模型表达式如下：

式中：Δw为桩土相对位移，ki1（kPa／mm），τi1（kPa），Δξ1（mm）分别为弹性阶段桩侧阻力传递系数、极限侧阻力及其相应的相对位移；ki2，τi2和Δξ2分别为强化（软化）阶段桩侧阻力传递系数、极限侧阻力及相应相对位移.而若相对位移较大（进入强化阶段），表明桩土已出现滑移现象.

考虑到桩端土体在承受荷载过程中出现的非线性变形特性，本文采用能够考虑桩底刚性层影响的双曲线荷载传递模型来近似模拟桩端处土体荷载－位移的非线性关系[6]：

式中：Pb为桩端荷载；υb为桩端土体泊松比；h为桩底至刚性层的距离；r0为桩身半径；Gb为桩端土体剪切模量；Pt为桩端极限荷载；Rt为双曲线曲拟合常数.

2 桩土分析的刚度矩阵分析

2.1 桩身总体刚度矩阵

将超长桩视为弹性杆件，按照桩周土层分布情况划分单元，为保证计算精度，每一土层再根据实际厚度情况划分为若干单元，至此可将桩身及相应桩周土划为n个独立单元，如图2所示.其中，桩土单元各n个，桩单元节点n＋1个，L为桩长，Li为各桩身单元长度.

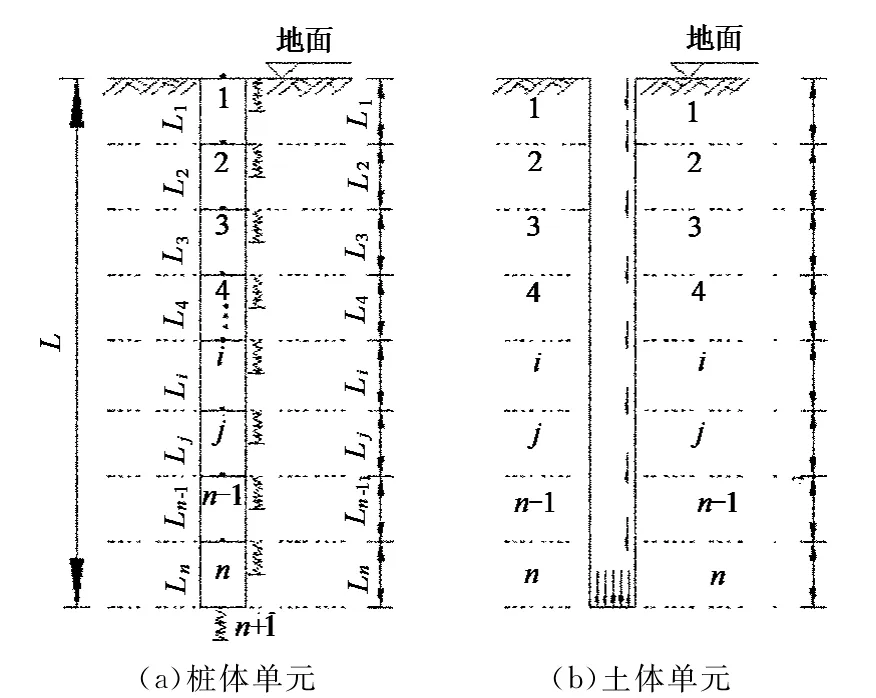
图2 单桩桩土计算模型Fig.2 The element of pile and soil

把外荷载Qi和桩侧摩阻力fi作用在n＋1个节点上，由于桩身单元可划分足够小，故假设任意桩身单元的桩侧摩阻力为均匀分布.集中摩阻力亦可以看做一集中力直接作用到单元上一个节点上.根据虚功原理，第i个桩单元的刚度矩阵为：

式中：Ep，Ap分别为桩身弹性模量及桩身截面面积.

各单元刚度矩阵可“对号入座”，构成桩身总体刚度矩阵[K]p，即：

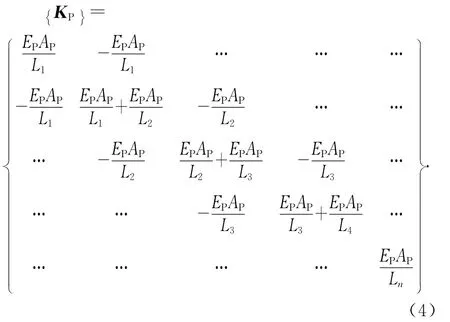
桩身整体位移方程为：

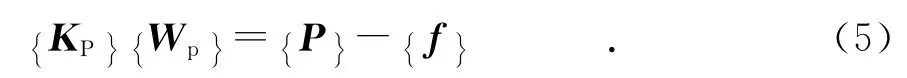
式中：Wp为桩身节点位移列阵；f为桩身节点的摩阻力列阵；P为桩身外荷载列阵.

2.2 土体总体刚度矩阵

为建立土体刚度矩阵需建立桩侧摩阻力与土体位移的关系式.众多学者[7－9]采用弹性半空间无限体的Mindlin解进行求解.基于Mindlin解的弹性理论法可计算不同深度处的位移相互影响，从而考虑了土体的连续性，但只限于均质土体；而超长桩所处地层分布极为复杂，往往由众多性质各异的土体构成，此外，当桩顶荷载逐渐增大时，桩周土体从上至下将逐渐进入塑性状态，桩土界面极限摩阻力亦从上至下先后发挥，此时某深度范围内桩周土体将发生塑性变形，显然Mindlin解的弹性理论亦未考虑桩周土体变形的非线性影响.

为解决桩周土体的成层性与非线性，本文采用τ－z曲线描述桩周土体承受摩阻力与本身变形之间的非线性关系.假定桩周土体在荷载作用下，其剪应力与剪应变呈双曲线关系，即土体割线剪切模量为[10－11]：

式中：G0为土体的初始剪切模量，MPa；τf为土体的破坏剪切应力；Rf为双曲线拟合常数.上述各系数均可通过简单的室内剪切试验确定.

当桩受荷后，桩周土中任意一点的剪应力随径向距离r（离桩中心的距离）的增大而减小，它们之间的关系可表示为：

式中：r0为基桩半径；τ0为桩周摩阻力.

桩侧土体位移与荷载的关系可表示为：

式中：rm为剪应力影响半径，Randolph与Wroth建议，rm＝2.5Lρ（1－μ），L为桩长，ρ为桩周土体非均质系数，ρ＝G（L／2）／G（L），μ为土体泊松比.

将式（6）和式（7）代入式（8）有：

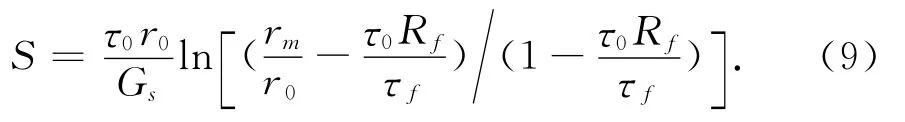
式中：S为桩侧土体的竖向沉降.

将桩周土体划分为n个独立单元，根据摩阻力与其竖向变形的关系式，建立其刚度矩阵.第i个节点处的桩侧土割线刚度表示为：

式中：τ0i可由位移桩侧荷载传递函数式（7）求出，节点i的初始刚度可表示为：

值得注意的是，式（11）是基于剪切位移法的基本假定而导出的公式，即假设桩土之间不存在相对滑移，但此处对单独的土体来说，考虑桩土滑移与否不会影响最终的土体位移计算结果.

桩端处土体的割线刚度采用类似方法求解，桩端处的初始刚度表示为：

故桩侧土的位移方程可以表示为：

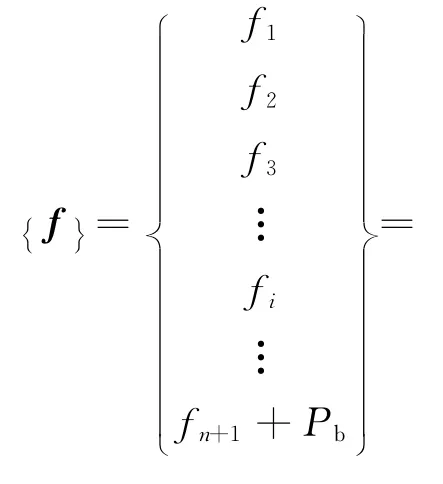
联立式（1），式（4），式（5）和式（13），即可得变形协调方程组；由于式（8）是一个非线性方程组，故不能直接求解，需迭代求解.

3 迭代求解过程

1）将桩顶荷载分级P01，P02，P03，…，P0i，…，P0n；根据式（10）和式（11）求得土体各节点初始刚度形成｛KS｝（0）；

2）将｛KS｝（0）代入桩土体系变形协调方程组，得｛WP｝（0），｛WS｝（0）以及｛τ｝（0）的具体数值；

3）依次计算各节点桩土相对位移Δwi.比较Δwi与Δξi1.若Δwi＜Δξi1，则桩土间未发生相对滑移，否则跳至步骤6）.由｛WS｝（0）根据式（3）与式（9）用二分法求得｛τ｝（1）和｛Pb｝（1），进而形成｛KS｝（1），并依次可得到｛WP｝（1），｛WS｝（1）以及｛τ｝（1）；

4）比较｛WS｝（0）与｛WS｝（1），若二者差值大于给定允许差值ε，则取｛WS｝（0）＝ ｛WS｝（1），形成｛KS｝（2），再重复进行步骤2）和3）；

5）若前后两次迭代计算过程的位移差值小于ε，则本级荷载P01作用下桩基位移为｛WP｝（1）；

6）若Δwi≥Δξi1，则桩土间已发生了相对滑移，根据桩土相对位移量判断发生相对滑移的节点个数，并对已滑移的桩段进行摩阻力重新赋值：若Δξi1≤Δwi＜Δξi2，则对相应节点上桩侧摩阻力赋值为τi1＋ki2（Δw－Δξi2）；而Δwi≥Δξi2时，则对相应桩土节点的桩侧摩阻力赋值τi2.重新迭代1）～5）中所述方法进行迭代计算，最后得本级荷载P01作用下｛WP｝（1），｛WS｝（1）以及｛τ｝（1）；

7）对于荷载P0i（i≠1），采用上一级荷载作用求的桩侧和桩端各节点的刚度作为本级荷载下计算的初始刚度，其后续具体计算步骤及方法与荷载P01作用相同.

4 算例验证

某大桥位于洞庭湖软土地区[12]，其试桩桩径1.0m，埋深60.0m，各主要土层至上而下依次为淤泥质粘土、粘土、细砂层、砂砾石及砂卵石.试验过程中，在各土层分界处埋设钢筋应力计以测试各点的桩身轴力并换算得出各土层摩阻力，而由桩体的弹性假设可得出各点的竖向变形，由此得出各土层τ－Δw关系曲线如图3所示.由图可知，各土层曲线发展趋势与应变硬化类曲线基本吻合，因此本文计算时采用该类曲线进行分析，先将弹性直线段末端对应的桩身变形量作为弹性变形临界值Δξ1，再把走势较平稳的塑性段各点拟合成水平直线，该直线与实测τ～Δw关系曲线的交点为塑性变形临界值Δξ2，各参数取值如表1所示.

图3 桩－土主要土层τ－Δw关系曲线Fig.3 Relationship betweenτandΔw

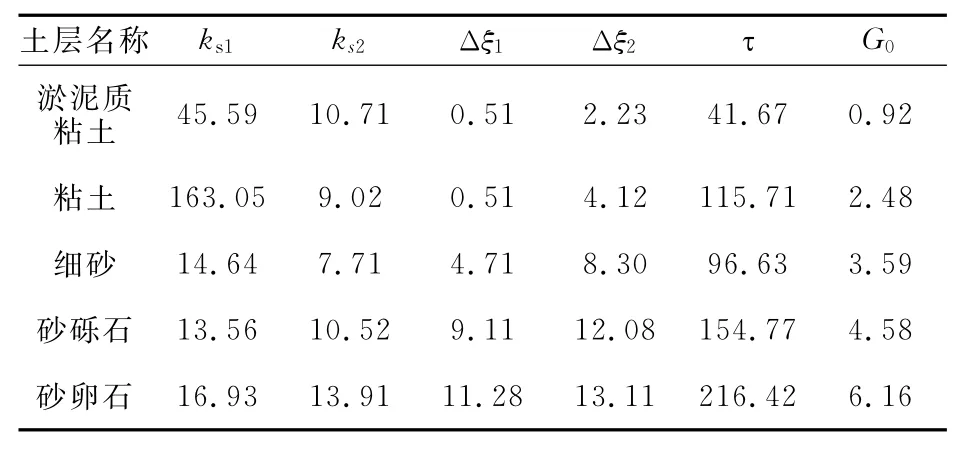
表1 各土层计算参数表Tab.1 The parameters of soils

试验过程中，按试桩的预计最大试验承载力等分为15级进行逐级等量加载，每级荷载为1 080 kN.按本文方法所获得的计算荷载－沉降曲线与实测对比如图4所示，本文计算得出的超长桩荷载－沉降规律与实测值基本吻合，各级荷载下桩顶沉降最大误差小于7%.

图4 试桩Q－s曲线实测值与计算值比较Fig.4 Calculated and measured load－settlement

5 结 论

考虑超长桩桩侧土体的成层性及不同的屈服特性，分别采用三折线模型及双曲线模型描述超长桩桩侧及桩端的荷载传递规律 .引入桩土滑移概念及τ－z理论曲线，对超长桩及桩周土分别划分单元进行离散化，建立了其整体刚度矩阵，并采用迭代法进行求解，从而提出了可模拟桩土滑移的超长桩非线性算法，该方法概念清晰，且可较全面地考虑超长桩的荷载传递特性.基于现场大型静载荷试验对本文方法进行了验证.对比数据表明，本文理论计算结果与实测值基本吻合，可在工程实际中应用.

[1] 王伯惠，上官兴.中国钻孔灌注桩新发展[M].北京：人民交通出版社，1999：1－9.WANG Bo－hui，SHANG Guan－xing.New development of bored piles in China [M].Beijing：China Communications Press，1999：1－9.（In Chinese）

[2] 林天健，熊厚金，王利群.桩基础设计指南[M].北京：中国建筑工业出版社，1999：11－13.LIN Tian－jian，XIONG Hou－jin，WANG Li－qun.Pile foundation design manual[M].Beijing：China Architecture ＆Building Press，1999：11－13.（In Chinese）

[3] 邓友生，龚维明.苏通大桥主塔超大群桩基础沉降特性研究[J].武汉理工大学学报，2008，30（7）：66－70.DENG You－sheng，GONG Wei－ming.Research on settlement of extra long large diameter pile groups under main tower of Sutong Yangtse river highway bridges[J].Journal of Wuhan University Technology，2008，30（7）：66－70.（In Chinese）

[4] 赵明华，刘齐建，曹喜仁，等.按桩顶沉降量控制超长灌注桩竖向承载力研究[J].工程力学，2006，23（2）：92－96.ZHAO Ming－hua，LIU Qi－jian，CAO Xi－ren，etal.Evalution of vertical bearing capacity of super long bored single pile by the pile head settlement[J].Engineering Mechanics，2006，23（2）：92－96.（In Chinese）

[5] KEDZI.Bearing mechanism of piles[J].Geotechnical，2004，26（1）：67－71.

[6] 王旭东，魏道垛，宰金珉.单桩荷载－沉降的非线性分析[J].南京建筑工程学院院报，1994，28（1）：15－24.WANG Xu－dong，WEI Dao－duo，ZAI JIn－min.Analysis of nonlinear load－settlement behavior of vertically loaded pile[J].Journal of Nanjing Architectural and Civil Engineering Institute，1994，28（1）：15－24.（In Chinese）

[7] 胡庆立，任瑞波，张克绪.轴向荷载作用下单桩沉降的非线性分析[J].工程力学，2006，21（3）：73－77.HU Qing－li，REN Rui－bo，ZHANG Ke－xu.Nonlinear analysis of settlement of axially loaded vertical piles[J].Engineering Mechanics，2006，21（3）：73－77.（In Chinese）

[8] 徐长节，黄洪超，蔡袁强，等.成层土中考虑桩土相对滑移的单桩沉降分析[J].岩土力学，2006，27（增刊）：803－808.XU Chang－jie，HUANG Hong－chao，CAI Yua－qiang，etal.Settlement analysis of single pile considering relative slipping in layered soil[J].Rock and Soil Mechanics，2006，27：803－808.（In Chinese）

[9] 吕凡任，陈云敏，梅英宝.一种基于Mindlin解的直桩沉降弹塑性分析方法[J].岩石力学与工程学报，2004，23（17）：2988－2991.LV Fan－ren，CHEN Yun－min，MEI Ying－bao.Elasto－plastic analysis method for vertical pile based on Mindin’s solution[J].Chinese Journal of Rock Mechanics and Engineering，2004，23（17）：2988－2991.（In Chinese）

[10] RANDOLPH M F，WROTH C P.Analysis of deformation of vertically loaded piles[J].Journal of Geotechnical Engineering Division，ASCE，1978，4（12）：1465－1488.

[11] KRAFT L M，RAY R P，KAGAWA T.Theoreticalz－τcurves[J].Journal of Geotechnical Engineering Division，ASCE，1981，107（GT11）：1543－1561.

[12] 赵明华，何俊翘，曹文贵，等.基桩竖向荷载传递模型及承载力研究[J].湖南大学学报：自然科学版，2005，32（1）：37－42.ZHAO Ming－hua，HE Jun－qiao，CAO Wen－gui，etal.Study on the load transfer model and the beovcng capacity of vertically[J].Journal of Hunan University：Natural Sciences，2005，32（1）：37－42.（In Chinese）