An innovative detection method of high frequency BPSK signal with low signal-to-noise ratio
2012-08-13SHIShuoXULizhenGUXuemaiZHANGHongli石徐立振顾学迈张宏莉
SHI Shuo,XU Li-zhen,GU Xue-mai,ZHANG Hong-li石 硕, 徐立振, 顾学迈, 张宏莉
(National Key Laboratory of Communication System and Information Control Technology,Harbin Institute of Technology,Harbin 150001,China)
Low signal-to-noise ratio signal detection is to obtain useful information of low signal-to-noise ratio signal in strong noise with detection methods.Here the“low signal-to-noise ratio signal”usually means that the Signal-to-Noise Ratio(SNR)is less than -10dB[1].Low signal-to-noise ratio signal detection has extensive and important applications,such as arming test under strong electromagnetic noise battlefield environment of information-based war,radar,micro electromechanical system(MEMS),GPS,earthquake,physic and so on[2].The BPSK(Binary Phase Shift Keying)signal is one modulation mode which is widely used in modern digital communication.It has good anti-jamming performance and high frequency band utilization rate.So it is necessary to study the detection method of low signalto-noise ratio BPSK signal.
One useful way to detect the low signal-to-noise ratio signal is to restrain the noise,such as correlative detection,narrowband filter and so on.With these methods,the noise is restrained.However,the useful signal is losing in the meantime.Thus,the non-linear theory is introduced into low signal-to-noise ratio signal detection.The non-linear theory,such as stochastic resonance[3],chaotic oscillator system[4],neural network[5]and etc,can detect the low signal-to-noise ratio signal by the cooperation of the signal and noise.Those non-linear methods are used to detect low signalto-noise ratio signal and get a great achievement.However,the signal frequency people have researched is very low,in an order of magnitude of 10 Hz to 102Hz.As is known to all,the transmission BPSK signal of the information-based war is usually a high frequency signal.Here by “high frequency”it means at least 3 MHz,and with the development of communication,such as air force communication,more attention needs to be paid to the higher frequency area.So this paper talks about detecting the low signal-to-noise ratio BPSK signal in high frequency area.In the three mentioned non-linear models,the stochastic resonance method is good at low signal-to-noise ratio signal detection.However,it usually simulates at a lower frequency area,which is not suitable for our research background.Neural network is mainly used in neural system,which is far more complex than the communication process.So this paper considers about the left method——chaotic oscillator method.
The chaotic theory has important status in the field of nonlinear science.For the chaos is nature category phenomenon,it is more common than orderly phenomenon,and chaotic theory can win people’s extensive concern.The chaos phenomenon has been found to exist in many nonlinear system,such as the integral equation and the differential equation which are common in mathematic.
In recent years many scholars in the communication field have dabbled in this area,and the research is mainly focus in chaos synchronization phenomenon and the secret communication of chaotic signals.Since the complexity of the research,they have not given any universal theory or robust criterion.
1 Fundamental Principle
Chaotic oscillator detection is a new signal processing method that is totally different from the existing various measurement methods.The chaotic system has some basic characteristics:
(1)Sensitive to the initial value:A tiny little change of the initial value can trigger large difference of the system with the time changed,and the most famous example is the“butterfly effect”.
(2)The boundedness:The random change tracks of chaotic system have certain bound,and the change of status does not affect the existing area of the tracks.
(3)The internal randomness:Use the given equations and the initial condition of the system,and the chaotic system may produce a random condition.
(4)The ergodicity:Chaotic motion has ergodicity in chaos attract domain,and the performance is that the track of the chaos can traverse all possible points of the system for the enough time.
(5)The positive Lyapunov exponent:The chaotic motion is corresponding to the positive Lyapunov exponent,while the periodic motion is corresponding to the negative Lyapunov exponent.
It mainly uses the extreme sensitivity of chaotic oscillator system on the initial conditions,by each initial condition corresponding to a trajectory.A tiny little change of the initial value can make the chaotic track change strikingly.By using this feature reversely,the minor change of the initial value can be measured.On the other hand,it is immune against the noise,which can make the system maintain current state while the noise changes.The theory mentioned above is the basic theory of chaotic oscillator detection.When the mixed signal goes into the chaotic oscillator system,we detect the existence and the feature of the low signal-to-noise ratio signal by the phase change situation and degree.
Of all the known chaotic oscillator systems,the Duffing-Holmes equation is a typical model which has been firstly used in the low signal-to-noise ratio signal detection[6].Due to the signal character and the equation’s format,we use the Duffing equation as the chaotic oscillator system model.The equation is as follows:

where k is damping ratio;-x(t)+x3(t)is non-linear resilience;γcos(t)is periodic driving force. The equation above describes the basic format of Duffing equation,in actual applications,and the γcos(t)in the equation may change into many forms of signals that is much more complex.
The system statusthatthe Duffing equation presents is extremely sensitive to the value of γ.To prove this character,we build the simulation system as shown in Fig.1.
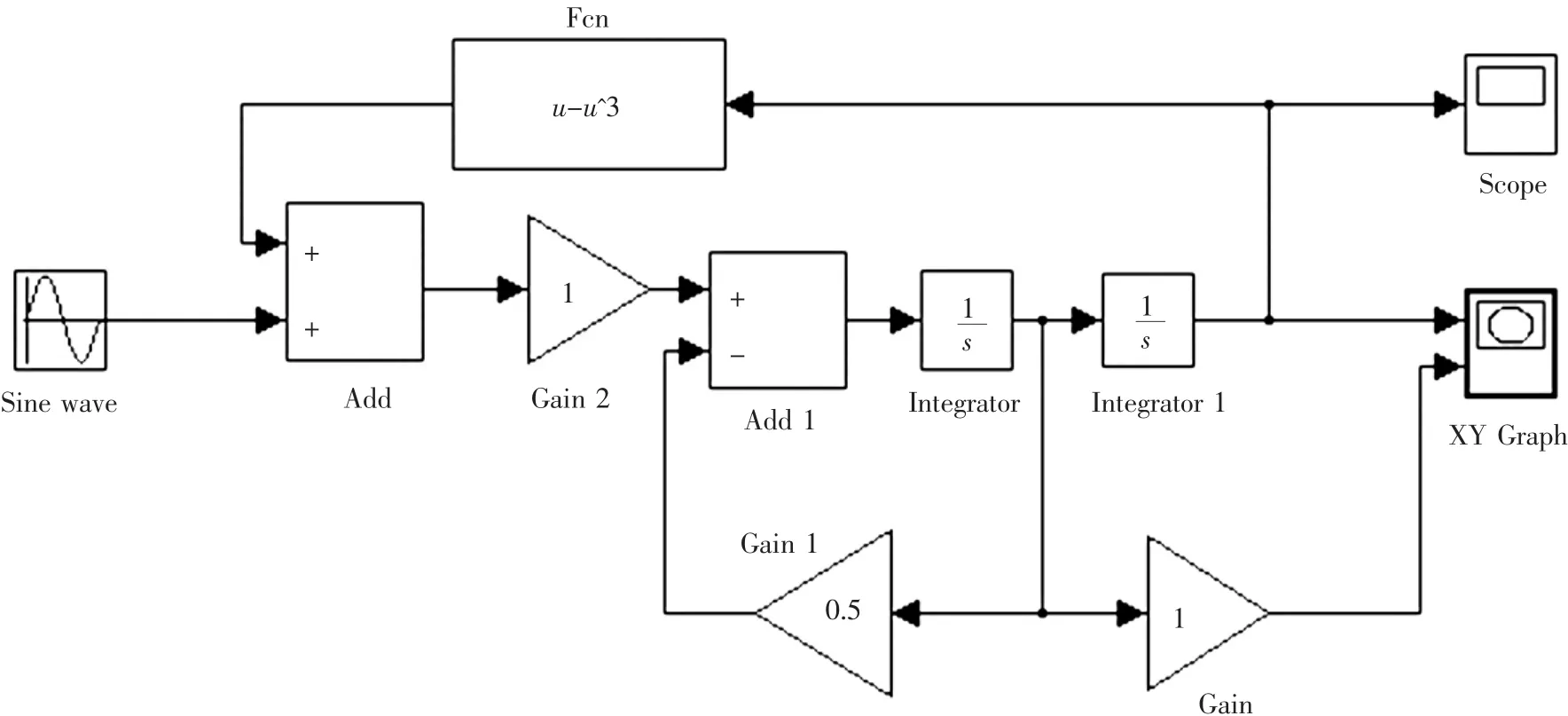
Fig.1 Simulation system
When k is a fixed value(here we make k=0.5),the status will change frequently with the change of γ,as shown in Fig.2.
According to the results in Fig.2,we can see that in some special values of γ,the status can change from chaotic state to the periodic state quickly,which can be a reliability criterion of the existing of low signal-tonoise ratio signals.
Let t= ω0τ and add the input signal as a part of periodic driving force,so we get the equation as follows:

where k is damping ratio;γcos(ω0t)is periodic driving force;ω0is the basic frequency of periodic driving force;Input=s(t)+n(t)is a low signal-to-noise ratio signal mixed with noise;s(t)is the low signal-tonoise ratio signal being detected;n(t)is the strong noise.

Fig.2 Phase track diagram
The situation mentioned above is that the periodic driving force and the low signal-to-noise ratio signal being detected have the same initial phase.However,if they have different initial phase,there can be non-detection zone.We can know from the formula derivation that π-arccos(a/2γd)≤ φ ≤ π +arccos(a/2γd)is the non-detection zone[7],where a is the signal amplitude;γdis the critical status;φ is the phase difference.
The BPSK(Binary Phase Shift Keying)signal is a common digital modulation mode,and the baseband signal deliver through the different phases of the carrier signal.The expression is shown as follows:

It uses signal phase to represent the different transmission base-band signal.Here we make phase 0 represents base-band signal‘0’,and then phase π represents base-band signal‘1’.In ideal state,the base-band signal‘0’and‘1’will have phase difference as π,which means they can not reach the nondetection zone at the same time,so we can use this character to identify the existence of BPSK signal.
For one signal chaotic oscillator model,if the base-band signal‘0’represents periodic state,the signal‘1’will be chaotic state,as shown above.We also know that chaotic state means that there is no frequency ω0signal to exist.To distinguish the two different situations,we use two chaotic oscillator models together to detect BPSK signals.The two chaotic oscillator models’parameters are mostly same,except one initial phase is 0 and the other initial phase is π.When a BPSK signal modulated by base-band signal‘0’or‘1’gets through the two models,the system states must present the opposite states.Considering about the two opposite states,we can identify the existence of BPSK signal,get the carrier frequency,and calculate the change time of base-band signals.Then we can recover the BPSK signal.
2 Detection Model
Through the analysis above,we know the basic principle of the improved method.Now we set up the detection model.
We define the critical value of γ as γd.When γ =γd,the system will be in the critical status from chaotic state to periodic state.Making the noise a part of the driving power can not change the phase path of the system.However,a tiny little change of the input low signal-to-noise ratio signal can make the phase path change apparently,so we can detect the existing of low signal-to-noise ratio signal.
We use the Lyapunov exponent to judge the chaotic state.When the max Lyapunov>0,the system is in chaotic state.And when the max Lyapunov <0,we think the system is being periodic.Then γ = γdequals the max Lyapunov=0,and the Lyapunov can be solved by QR decomposition algorithm.
Usually we make k=0.5,and we can sed as shown in Fig.3.
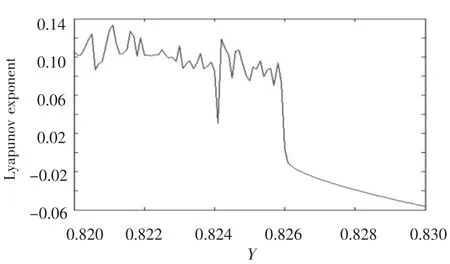
Fig.3 Relation between γ and the max Lyapunov
From Fig.3,we know that γd=0.8260.
To detect the BPSK signal,we use two chaotic oscillator models together.The chaotic oscillator model is as Eq.(2)describes,and we can set up the detection system as Fig.3.
We define the max Lyapunov exponent of BPSK signal detection system to be the minimum of the two chaotic oscillator models max Lyapunov.When it is always below 0,the BPSK signal exists.
To judge the change time of base-band signals,we use the different states of the two chaotic oscillator models.We call the upper chaotic oscillator model as model 1,and the other is model 2.Different base-band signals make the two models state change,meanwhile the two models state remain opposite.So we can get the base-band signals of the BPSK signal.
3 Simulations
We use the program in Fig.4 to simulate the process.Choose parameters:the driving force amplitude γd=0.8260;frequency f0=400 MHz;damping ratio k=0.5;the initial phase of Sine Wave model is 0;the initial phase of Sine Wave model is π.
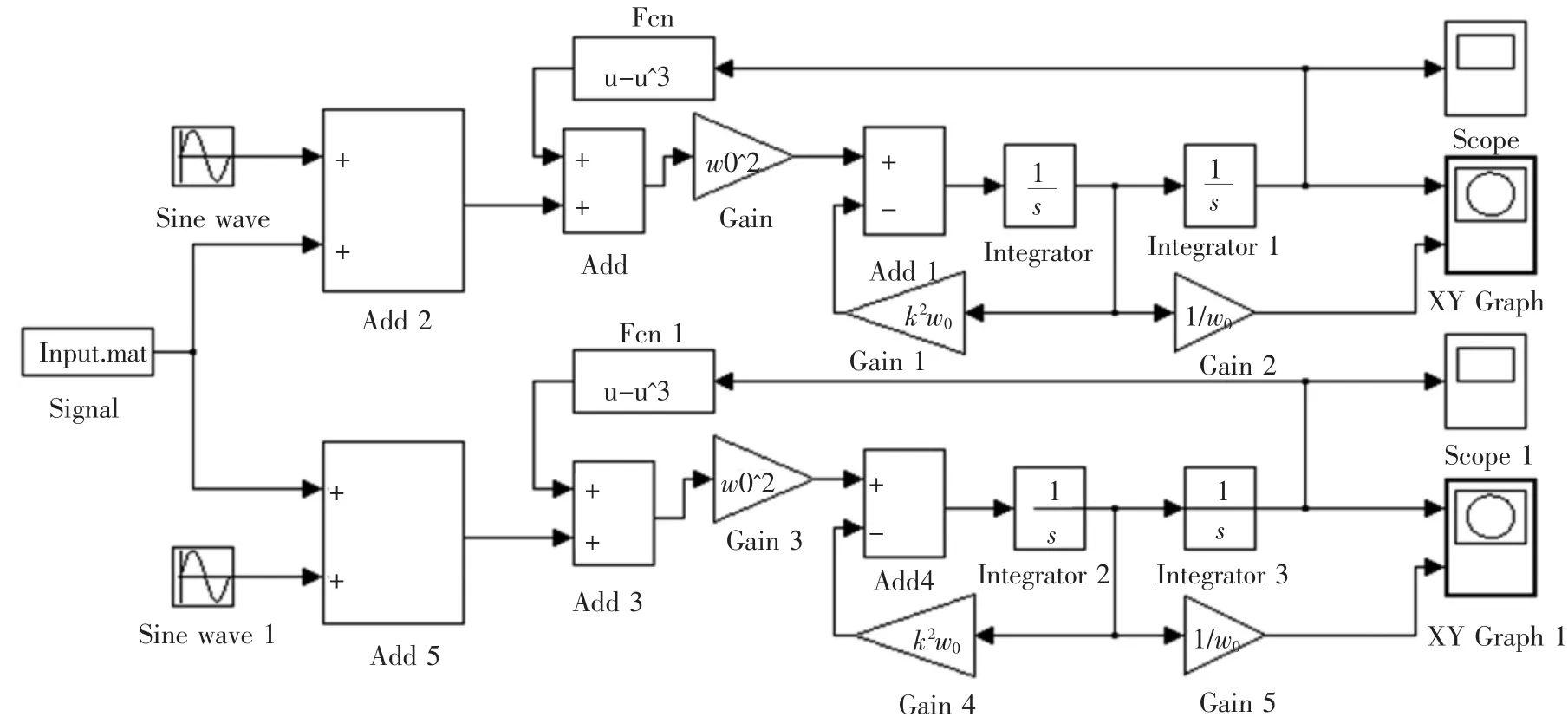
Fig.4 BPSK signal detection system
Signal-to-Noise Ratio is used to describe the processing result.The relative equation is:

where A is the signal amplitude;D is the noise variance.
The input signal is BPSK signal with strong noise.A BPSK signal can be described by the equation below:

Here the input signal is s(t)=0.05sin(2πft+φ)+n(t),where the signal frequency f=f0=400 MHz;n(t)is the Gaussian white noise,φ =
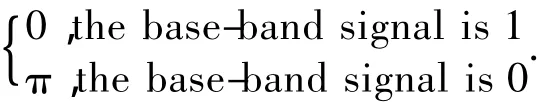
1)The input Signal-to-Noise Ratio is -10 dB.The base-band signals are random,as shown in Figs.5 and 6.It is the signal mixed with strong noise,which will be put into the simulation system.
We get the system state changing oscillograms and the phase track diagrams of chaotic model 1 and chaotic model 2,as shown in Fig.7.
Based on the phase track diagrams of the two models as shown in Figs.6(b)and 6(d),we can finally get the max Lyapunov of detection system,as shown in Fig.8.
For the max Lyapunov of detection system is always below 0,we can say that the BPSK signal exists,and its carrier frequency is 400 MHz.

Fig.5 Random base-band signals when SNR=-10 dB

Fig.6 Input BPSK signals mixed with noise when SNR=-10 dB

Fig.7 Detection results when SNR= -10 dB
Then we can judge the change of base-band signals by the changing states.Here we use the changing state which changes from chaotic state to the periodic state quickly to judge the change of base-band signals.To the chaotic oscillator model 1 as shown in Fig.7(a),the changing state means that input base-band signals change from‘0’to‘1’.To the chaotic oscillator model 2 as shown in Fig.7(c),the changing state means that input base-band signals change from‘1’to‘0’.We should also use the opposite states of the two models in every time to subtract the wrong judgment.Then we can get the recovered base-band signals,as shown in Fig.9.
Through the comparison between the results shown in Figs.5 and 9,we can see that the signal has been recovered.

Fig.8 System max Lyapunov Exponent when SNR= -10 dB

Fig.9 Recovered base-band signals when SNR= -10 dB
2)The input Signal-to-Noise Ratio is -20 dB,and the base-band signals are random.
The signal in Fig.10 is the base-band signal,and the signal mixed with strong noise is shown in Fig.11,which will be put into the system.
We get the system state changing oscillograms and the phase track diagrams of chaotic model 1 and 2,as shown in Fig.12;the system max Lyapunov,as shown in Fig.13.
From Fig.12,we can say that the BPSK signal exists,and its carrier frequency is 400 MHz.
We can also get the recovered base-band signals by Figs.12(a)and 12(c),as shown in Fig.14.
Through the comparison between the results in Figs.10 and 14,we can see that the signal has been recovered.

Fig.10 Random base-band signals when SNR= -20 dB

Fig.11 Input BPSK signals mixed with noise when SNR=-20 dB
But through the observation of phase track in Figs.12(b)and 12(d),we should know the system has been seriously affected by the strong noise.
If we reduce the SNR of the signal further,the system may not detect the existence of the weak signal,for the system has been seriously polluted by the noise.
4 Conclusions
The present method is a new attempt,based on this unique method we can detect the low signal-tonoise ratio BPSK signal in high frequency area.The simulation results show that the carrier frequency of the detectable BPSK signal can be 400 MHz,and the input SNR threshold can be -20 dB.Further research should be done to enhance the frequency magnitude and to lowerthedetectable input Signal-to-Noise Ratio.

Fig.12 Detection results when SNR= -20 dB

Fig.13System max Lyapunov Exponent when SNR= -20 dB
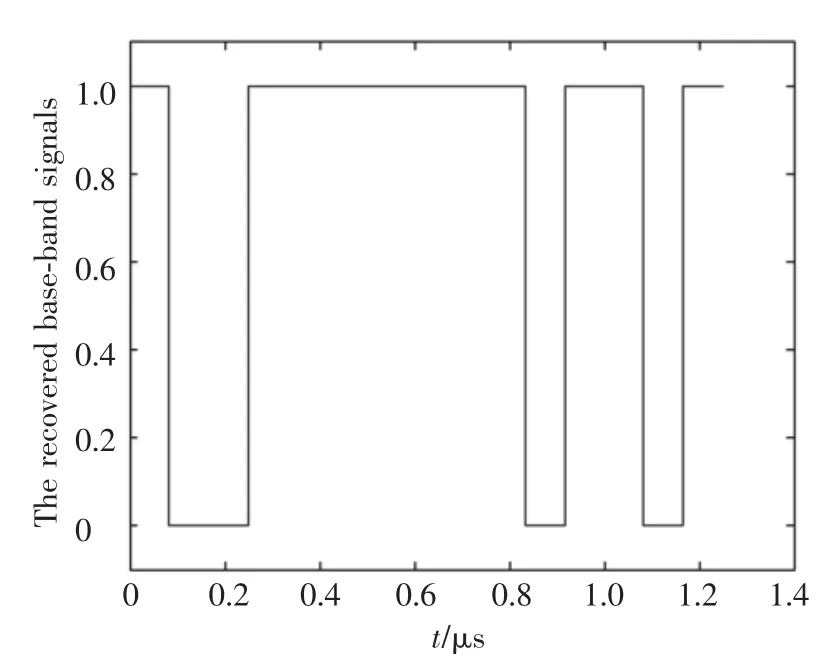
Fig.14 Recovered base-band signals when SNR= -20 dB
[1]Li Yue,Yang Baojun.Introduction of Chaotic Oscillator Detection.Beijing:Publish House of Electronics Industry,2004.
[2]Wang Guanyu,Chen Dajun,Lin Jianya,et al.The application of chaotic oscillators to weak signal detection.IEEE Transactions on Industrial Electronics,1999,46(2):440-444.
[3]Zhou Yurong,Guo Feng,Jiang Shiqi.Stochastic resonance of a linear system with colored noise.Journal of University of Electronic Science and Technology of China,2008,37(2):232-234.
[4]Li Yue,Yang Baojun.Chaotic system for periodical signal detection under strong noise background.Journal of Chinese Science Bulletin,2003,48:19 -21(in Chinese).
[5]Hummels D M,Ahmed W,Musavi M T.Adaptive detection of small sinusoidal signals in non-Gaussian noise using an RBF neural network.IEEE Transactions on Neural Networks,1995,6(1):214 -219.
[6]Shang Qiufeng,Yin Chengqun,Li Shilin.Study on derection of weak simusoidal signal by using duffing oscillator.Proceedings of the CSEE,2005,25:66 -77.
[7]Liu Wenbo.The Chaotic Sensors.Science and Technology.Report of Aeronautics and Astronautics,2000.
杂志排行
Journal of Harbin Institute of Technology(New Series)的其它文章
- Journal of Harbin Institute of Technology(New Series)
- Design and realization of lamp life test instrument
- A modeling method of microburst based on multiple vortex ring
- Remediation of static lake water by intensified filter of dominant bacteria colony
- A reliable and high throughput hybrid routing protocol for vehicular ad-hoc network
- Research on the Seebeck effect in efficient turning process and improving tool life
