A modeling method of microburst based on multiple vortex ring

LIN Lian-lei，YAN Fang

林连雷， 闫 芳

(Dept.of Automatic Test and Control，Harbin Institute of Technology，Harbin 150001，China)

Microburst is a special kind of low-level wind shear，which induces an outflow of strong wind near the ground and can do great damage to aircrafts.Microburst wind encountered during landing or takeoff has been a contributing factor in several major commercial airline accidents［1］.A mathematical model of a microburst can help evaluating and reducing the damage.There are many methods to simulate microburst，such as RANS based simulation method［2］， harmony superposition method［3］，and vortex ring model based methods［4－5］.

The most widely used microburst model is the vortex ring model，which was firstly proposed by Woodfield and Wood［4］.A pair of vortex ring is used to model a microburst.Usually we use the improved multiple vortex ring model to make the microburst be closer to the actual situation.A parameter selection algorithm is used to determine the numerical values of the model parameters.In Ref.［1］，the parameters were determined under the least squared-error rule，which could be solved by the Newton-Raphson algorithm［6］.A parameters selection method of multiple vortex microburst was proposed based on experiential formula，but it was not flexible［7］.The model parameters selection was seemed as a optimization problem［8］，and the particle swarm optimization(PSO)was introduced to solve the parameters selection problem，and got a nice result.Inspired by the results in Ref.［8］，we propose a differential evolution(DE)based parameters selection method in this paper.

Differential Evolution(DE)［9］is a global optimization algorithm，which in many optimization problems has shown better performance than SA，GA，PSO and other algorithms.In recent years，DE and modified DE［10］have been widely used in many fields，such as antenna configuration［11］，high scale dynamic optimization［12］，classification of power quality［13］，and so on.DE has shown better performance than simulated annealing(SA)，genetic algorithm(GA)，PSO and other algorithms in many optimization problems.

In this paper，a parameter selection algorithm suitable for virtual flight simulations is proposed.We choose the maximum velocity as the goal characteristic，and introduce differential evolution algorithm into the selection of the parameters of multiple vortex ring microburstmodel.Whereasthe nested optimization process when selecting the parameters，a nested DE algorithm is proposed and utilized in selecting the parameters of multiple vortex ring microburst model.

1 Multiple Vortex Ring Model of Microburst

The vortex ring model uses a pair of vortex rings to induce the microburst flow，as shown in Fig.1.The model places a vortex ring filament above the ground plane at the distance of H，and an image ring filament at the distance of－H，with the intensity of±Γ，and the radius of R.Each vortex ring pair(primary and image)shares a common central axis in the flow-field.The wind velocity induced by a vortex ring pair is computed by evaluating the derivatives of a combined vortex ring stream function［14］.

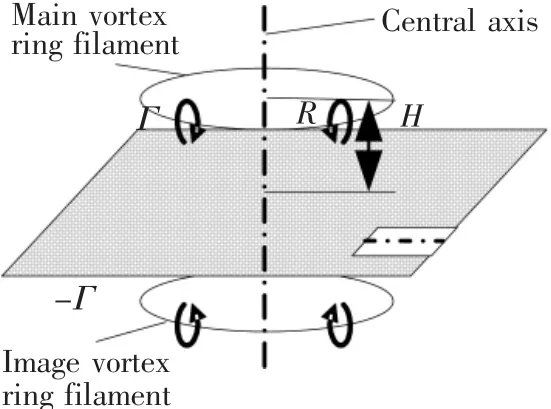
Fig.1 Illustration of vortex ring model

For a single vortex ring pair，the wind velocity components induced at a point at(x，y，z)are given by

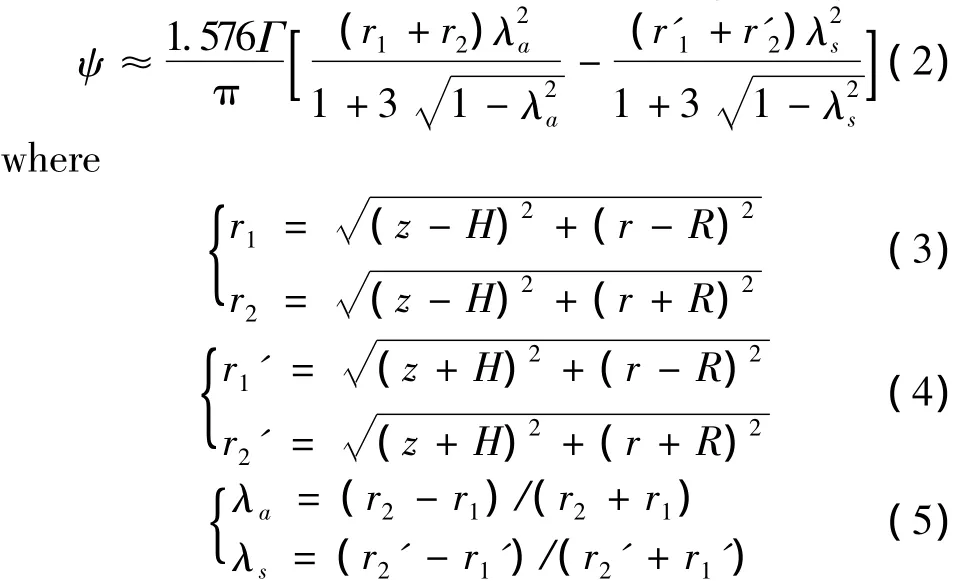
The researches show that for the flow field induced by a single pair of vortex ring，the vertical velocity is small relative to the horizontal velocity intensity［15－16］.To improve the model，multiple vortex ring model is proposed，which is consist of multiple vortex ring pairs.It is assumed that a microburst is induced by n pairs of vortex ring.The wind component induced at a point(x，y，z)by the ith vortex ring pair is Vi= ［vix，viy，viz］，and then that induced by n pairs of vortex ring is

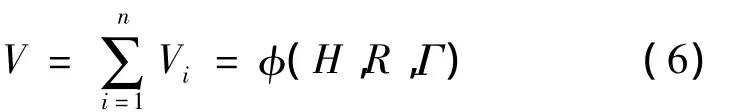
where H ={Hn}is the height of each vortex ring pairs;R ={Rn}is the radius of each vortex ring pairs，and Γ ={Γn}is the intensity of each vortex ring pairs.The parameter vector is defined as

2 Parameter Selection of Multiple Vortex Ring Model

2.1 Analysis of Parameter Selection

The characteristic of the induced microburst is determined by the parameters of vortex ring pairs.So it is necessary to select the parameters according to the simulation requirements.

The maximum velocity of a microburst represents its intensity.It can be used to evaluate the damage of a microburst to the aircraft.Therefore we choose the maximum velocity as the goal of global optimization in our parameter selection algorithm of multiple vortex ring microburst model.The process of our algorithm can be described as follows:firstly，initial the parameter vector p，and then find out the maximum wind velocity under the parameter.If the value of the maximum wind velocity meets the value we set，take it;otherwise，update a new parameter vector p’and select it again.This is an optimization problem.For a given model parameter vector，the wind velocity is different on different position.Thus，in order to find the maximum wind velocity，we need to find the position(x，y，z)where maximum wind velocity comes up，which is also a optimization problem.

It can be seen that in the whole process，there exist two interrelated optimization processes.Standard DE cannot solve nested optimization problem like this.Therefore，we improve the standard DE algorithm by using nested DE algorithm.

2.2 Nested DE Algorithm

From the above discussion，we know that there are two interrelated optimization processes in the parameter selection algorithm:one(target optimization)is to looking for the optimal parameters of the model H，R，Γ，which is the ultimate goal;the other(intermediate optimization)is to looking for the position of maximum velocity for each model parameters.

In order to accomplish both the target optimization and the intermediate optimization simultaneously，we improve the standard DE algorithm［9］to a nested DE algorithm.For the word“nested”，it means that in the selection possession of the standard DE algorithm，a different possession DE is implied.

Two vector populations are needed for nested DE:one for the target optimization and one for the intermediate optimization.In general，it is assumed that M={m1，m2，…，md1}is the parameter vector for target optimization，and X={x1，x2，…，xd2}is the parameter vector for intermediate optimization，while F(M，X)is the cost function for target optimization，and f(Mi，X)is the cost function for intermediate optimization for the vector Mi，and then the relationship between target vector population and intermediate vector population is shown in Fig.2.

In the standard DE algorithm，three constant parameters α，pcand P take control of the process.Among them，the value of α and pcaffect the robustness and convergence speed of DE，where optimal value depends on the vector population size P.A larger P brings a result to be closer to the minimum，but the population converges slower，while a smaller one may make the optimize process stop before it find the optimal result.For these reasons，in nested DE，a reasonable larger intermediate vector population size ensures the accuracy of the results，while a smaller target vector population size improves the efficiency of the algorithm.

Fig.2 Relationship between target vector population and intermediate vector population

2.3 Parameter Selection Algorithm Based on Nested DE

For the parameter selection algorithm of multiple vortex ring microburst model based on nested DE proposed，target vector is the microburst model parameter vector p，while intermediate vector is the coordinate of a point of the model(x，y，z).We detail the algorithm as follows:

Step 1 Randomly choose the initial target vector population{H，R，Γ}.

Step 2 Randomly choose the initial intermediate vector population(x，y，z)for each target vector generated in the previous step.

Step 3 Look for the position where we get the maximum velocity using the standard DE algorithm，and then mark the coordinate(x'，y'，z').Go to next step when the intermediate optimization’s termination condition is satisfied.

Step 4 Compute the cost function of the target vector population.

Step 5 If the target optimization’s termination condition is satisfied，export the optimal model parameters and quit，else，update the target vector and then go to Step 2.

Termination condition for target optimization is that the error of maximum velocity between the model induced and set value is within the range ΔvTset by the user.For intermediate optimization，the error between N consecutive velocity is within the range ΔvI.ΔvT，ΔvIand N，which are all set by the users according to the accuracy requirement of the flight simulation so as to make the algorithm very flexible.

3 Numerical Experiments

The microburst velocity field induced from the multiple vortex ring model is symmetrical about the central axis of the vortex ring.Therefore，we choose the plane xoz to compute the velocity in the numerical experiments.Then vy=0，which makes the calculation simple.

In the numerical experiments，we give an example of a microburst model which consists of two vortex ring pairs.The velocity induced at the point(x，y，z)is

where v1and v2are the velocity induced by the first and the second vortex ring pair，getting from Eqs.(1)－(6).The cost equation for target optimization is

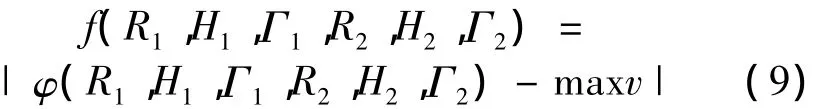
where maxv is the maximum velocity of the microburst which we want to achieve through the parameter selection algorithm.Until the termination condition f＜ ΔvTis satisfied，the optimal parameters of multiple vortex ring model of microburst are exported.In the following experiments，ΔvT=1 ×10－3m/s is set.

The control parameters of nested DE algorithm are shown in Tab.1.In the first experiment，we test the accuracy of the parameter selection algorithm proposed in this paper.Fig.3 shows the velocity vector graph of the microburst when the maximum v=25 m/s is set.

Tab.1 Control parameters of nested DE

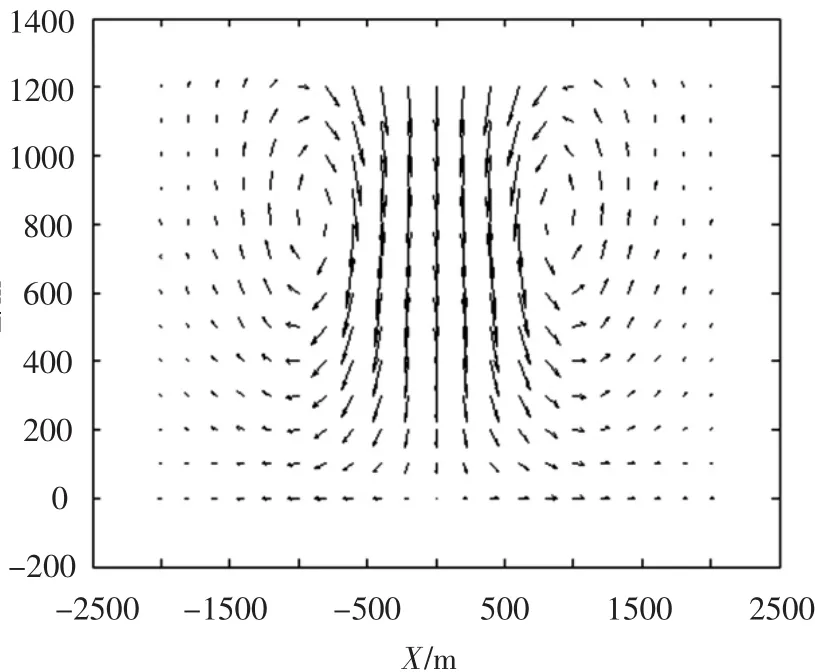
Fig.3 Velocity vector graph when max v=25 m/s

Fig.3 shows the contour of the velocity field of the induced microburst has the same characteristics with the actual microburst.The result is in accordance with the observational data from Refs.［17 －18］.

In the second experiment，we test the parameters of the multiple vortex ring microburst model.We choose the maximum v=10 m/s，20 m/s and 30 m/s.The parameters are shown in Tab.2.

Tab.2 Parameters of the multiple vortex ring microburst model get by our algorithm

From Tab.2，we can see that the error between the maximum velocity of the microburst and the set one is within the error range.We can get the microburst which we need through the algorithm in this paper.

4 Conclusions

In this paper，we propose a parameter selection algorithm for multiple vortex ring of microburst model，which is more suitable for virtual flight simulation than the existing algorithm.To solve the interrelated optimization problems，a nested DE algorithm is proposed and utilized.Through this parameter selection algorithm，we can get microburst whose maximum wind velocity meets the value we set.Several experiments show that this parameter selection algorithm is both flexible and accurate.

［1］Schultz T A.Multiple vortex ring model of the DFW microburst.Proceedings of the AIAA 26th Aerospace Sciences Meeting.Ames Research Center，AIAA Paper 88 － 0685.1988.

［2］Qu W，Ji B.Numerical study on formation and diffusion wind fields for thunderstorm microburst.Proceedings of International Conference on Mechanic Automation and Control Engineering(MACE2010).Washington DC:IEEE Computer Society，2010.1389－1392.

［3］Ji B，Qu W.Study on numerical simulation of fluctuating wind for thunderstorm microburst using harmony superposition method.Proceedings of the International Conference on Mechanic Automation and Control Engineering(MACE2010).Wuhan，China:IEEE Computer Society，2010.1233－1236.

［4］Woodfield A A，Woods J F.Worldwide experience of wind shear during 1981－1982.Proceedings of the AGARD Flight Mechanics Panel Conference on“Flight Mechanics and system design lessons from Operational Experience”.AGARD CP No.347.1983.

［5］Nguyen H，Manuel L，Veers P.Simulation of inflow velocity fields and wind turbine loads during thunderstorm downbursts.Proceedings of the Structural Dynamics and Materials Conference.Orlando，FL:American Institute of Aeronautics and Astronautics Inc，2010.

［6］Mehta R S.Modeling clear-air turbulence with vortices using parameter-identification techniques.Journal of Guidance，Control，and Dynamics，1987，10(1):27 －31.

［7］Zhu Shangxiang.The hydrokinetics model of microburst.Flight Dynamics，1984，(2):59 －72.

［8］Wu Y，Jiang S.Parameters selection method of multiple vortex-ring microburst model based on nested particle swarm optimization.Chinese Journal of Electronics，2012，40(1):204－208.

［9］Storn R，Price K.Differential evolution-A simple and efficient heuristic for global optimization over continuous spaces.Journal of Global Optimization，1997，11(4):341－359.

［10］Ramezani F，Lotfi S.The modified differential evolution algorithm(MDEA).Lecture Notes in Computer Science，2012，7198:109－118.

［11］Develi I，Yazlik E.Optimum antenna configuration in MIMO systems:A differential evolution based approach.Wireless Communications and Mobile Computing，2012，12(6):473－480.

［12］Raciborski M，Trojanowski K，Kaczynski P.Differential evolution for high scale dynamic optimization.Lecture Notes in Computer，2012，7053:180 －189.

［13］Biswal B，Behera H，Bisoi R，et al.Classification of power quality data using decision tree and chemotactic differential evolution based fuzzy clustering.Swarm and Evolutionary Computation，2012，4(6):12 －24.

［14］Ivan M.A ring-vortex downburst model for flight simulations.Journal of Aircraft，1986，23(3):232 －236.

［15］GAO Zhenxing，GU Hongbin.Research on modeling of microburst for real time flight simulation.Journal of System Simulation，2008，20(33):6524－6534.

［16］Zhu Shangxiang，Etkin B.Model of the wind field in a downburst.Journal of Aircraft，1985，22(7):595 －601.

［17］Liu Hongen.Characteristics and numerical simulation of microburs.Acta Meteorologica Sinica，2001，59(2):183－196.

［18］Zou Bo.Characteristics of microburst.Journal of Civil Aviation University of China，2002，20(3):28－31.