极小BTb参数GMSK信号的非相干解调

孙继民， 王世练， 朱 江

（①国防科技大学电子科学与工程学院, 湖南 长沙 410073；②武警8740部队, 四川 南充 637000）

0 引言

研究BTb小、频谱效率高的GMSK信号解调方法意义重大，尤其是未来高速深空传输和带限FDMA卫星通信系统。

目前对0.25≤BTb≤0.5的GMSK信号解调的研究较多[1-3]，但针对BTb≤1/6时GMSK信号解调的研究不多[4-5]。针对极小BTb参数GMSK信号的解调，研究了基于相位差分和Viterbi检测的非相干解调方法，给出了不同了BTb下Viterbi检测的状态转移计算方法，对其进行了性能分析和计算机仿真。

1 相位差分GMSK解调

1.1 单比特相位差分解调

接收到的GMSK信号可表示为：

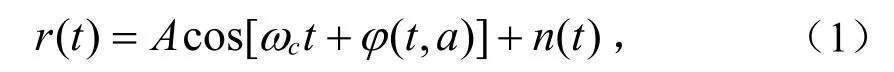
式中，A表示信号的包络常数，φ(t, a)是GMSK信号的瞬时相位，nc( t)和ns( t)分别为窄带噪声信号的同相和正交部分。

图1中的时延取Tb，相移π/2，不考虑噪声影响，低通滤波后输出：

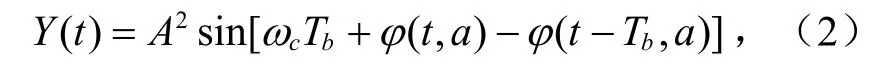
式中，φ(t, a)-φ( t-Tb, a)表示相位路径在1 bit信息码元内的变化。假设接收机不存在残留频偏或者满足ωcTb=0，则：

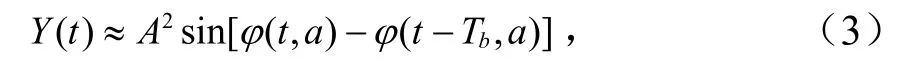
门限判决准则为：

1.2 2比特相位差分解调

与单比特差分解调相似，图1中的延时为2Tb，相移0，低通滤波后输出为：

由文献[5]得知2比特差分解调时Y( t)的基带波形是不对称的，门限判决需要引入一个直流偏置υ，相应的判决准则为：

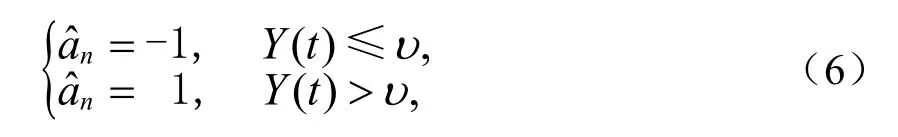
相对 1比特相位差分法，2比特相位差分法解调性能有明显改善[6]。

2 基于相位差分的Viterbi检测

BTb≤0.25时的码间串扰ISI较大，上述门限硬判决的误码率高，采用MLSE检测可以大大提高其解调性能。

2.1 单比特相位差分的Viterbi检测

令t=kTb，从式（3）中提取瞬时相移信息φk(t)=φ(t, a)-φ(t-Tb, a)，采用Viterbi[7]算法实现MLSE检测。考虑当前码元对其前后L个码元的ISI，则第k个码元的相移φk可表示为：式中，ak为输入码元，kβ为加性高斯白噪声引入的相位分量的变化值，iφ表示码元对相位的影响：

Viterbi检测仅考虑当前码元前后L′(1≤L′≤L)个码元的ISI影响，约束长度为2L′，检测器状态有N=22L′个。在每个码元结束时，有2N种状态转移可能，需计算2N条路径度量。码元ak对相位的影响从k-L′个码元间隔开始，则从式（3）中提取瞬时相移信息先经L′ Tb的时延后计算到达每个状态的支路相位度量，与上一状态的幸存路径累加获得各状态转移支路的总路径度量，依据路径度量最小原则选择该状态的当前幸存路径。

Viterbi检测求得的幸存路径就是所要寻找的正确的相位路径。对于任何L′的取值，在第k个码元间隔的状态为与前2L′个符号有关，定义为Sk=(ak-2L′,ak-2L′+1,…,ak-1)。从状态Sk转移到状态Sk+1，所对应的支路相位度量定义为：

式中，P( Sk,Sk+1)表示在理想条件下，从状态Sk转移到状态Sk+1对应输入不同符号序列的标准值。

序列d=(dk-2L,dk-2L+1,…,dk)表示从状态Sk转移到状态Sk+1对应的不同符号序列，不同BTb所对应的φi由式（8）和式（9）求得，对应的φi值见表1。

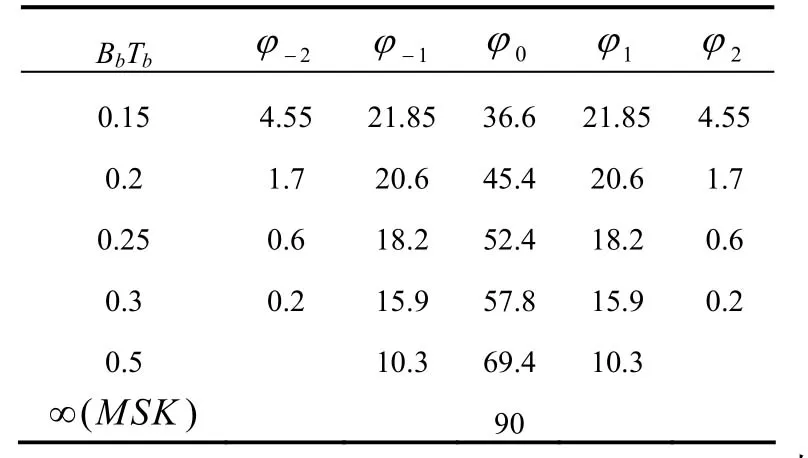
表1 1比特差分不同BTb对应的iφ值

第k+1个码元的总相位路径度量M( Sk+1)与第k个码元间隔存储的幸存路径度量M( Sk)之间的关系为：

Viterbi检测即按式(10)、式(11)和式(12)构成的迭代关系逐次计算在每个码元时间间隔Tb内各状态所对应的相位路径度量，依照路径度量最小的原则选取各自的幸存路径。该迭代计算过程进行N次后，获得的总的幸存路径也就是解调出的GMSK的相位路径。从而解调出信息序列aˆn。

2.2 2比特相位差分的Viterbi检测

2比特相位差分的Viterbi检测与单比特相位差分的Viterbi检测方法类似。首先从式（5）中提取瞬时相移信息为φk(t)=φ(t)-φ(t-2Tb)，考虑当前码元对其前后L个码元的ISI，第k个码元间隔内的相移φk为：

式中，ak为输入码元，kξ为加性高斯白噪声引入的相位分量的变化值，iφ表示码元对相位的影响为：

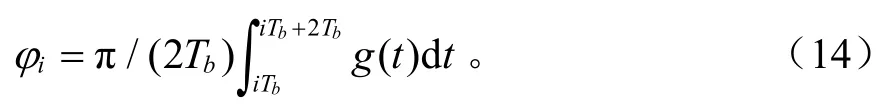
仅考虑当前码元前后L′(1≤L′≤L)个码元的ISI影响，由式(13)可看出φk(t )受到码元ak后面L′个码元以及前面L′+1个码元的影响, 则检测器状态有N=22L′+1个。从状态Sk转移到状态Sk+2，所对应的支路相位度量定义为：

式中，P( Sk,Sk+2)表示在理想条件下，从状态Sk转移到状态Sk+2对应输入不同符号序列的标准值：

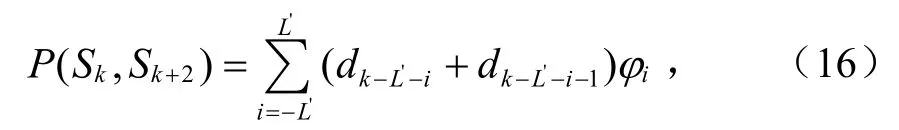
序列d=(dk-2L-1,dk-2L,…,dk)表示从状态Sk凡转移到状态Sk+2所对应的不同符号序列，其中不同 BTb所对应的φi由式（9）、式（14）求得，对应的φi值见表2。

表2 2比特差分不同BTb对应的iφ值

3 仿真及分析

3.1 较大BTb条件下的门限判决

分别取BTb为0.25和0.5，GMSK采用波形存储法调制产生，同一信噪比下实验1 000次，每次105bit。图2给出了1比特相位差分(1 bit DPD)、2比特相位差分(2 bit DPD)的系统解调误码率仿真结果，图2中同时给出了BTb=0.25时GMSK相干解调的误码率下界[8]：

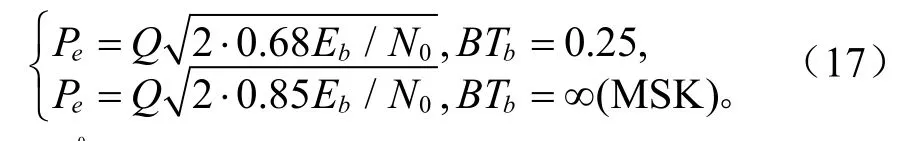
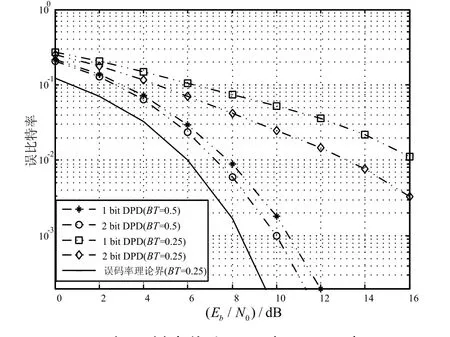
图2 门限判决差分GMSK解调误码率

不难看出：采用2比特相位差分法解调的性能优于1比特相位差分法，两者适用于较大BTb下的GMSK信号解调；BTb较小时，门限判决无法消除码间串扰的影响，系统解调性能明显恶化。

3.2 极小BTb条件下的Viterbi检测

分别取BTb为0.25和0.5，其他条件同上。图3给出了基于Viterbi检测的差分GMSK解调误码率结果，1比特相位差分法的约束长度取5Tb，2比特相位差分法的约束长度取4Tb。可以看出，BTb较小时，基于Viterbi算法的MLSE检测可以有效地消除码间串扰影响，系统解调性能明显改善，相比相干解调的误码率，BTb=0.25时的解调信噪损失小于1 dB；BTb=0.15时，基于 Viterbi检测的 2比特相位差分（2 bit DPD VD）比1比特相位差分（1 bit DPD VD）的性能有明显提高。综合考虑算法实现复杂度，BTb=0.15时，采用2比特相位差分、约束长度为4Tb的Viterbi检测是较好的解决方案。

图3 Viterbi检测差分GMSK解调误码率

4 结语

针对BTb参数较小GMSK信号的非相干解调，研究了基于门限判决和Viterbi检测的差分GMSK解调方法，给出了具体的实现方案和相应的计算机仿真结果，可有效地应用于深空通信中的地面遥测接收机设计。下步研究可针对BTb参数较小GMSK信号的干解调。有两个方向：①利用Laurent分解将信号近似线性表示，使信号简化成OQPSK信号解调；②利用Laurent分解简化维特比接收机进行检测。相干解调性能优于非相干解调，难点在于载波跟踪和位定时同步。

[1] 邓鹏, 李挥,安辉耀. GMSK解调系统中维特比均衡器的设计与优化[J].通信技术,2010, 43(02):43-45.

[2] FONSEKA J P. Noncoherent Detection with Viterbi Decoding for GMSK Signals[J]. IEEE Proc-Commun,1996,143(06):373-379.

[3] 韦道知.跳频系统GMSK调制解调技术的研究与实现[D].西安：西安电子科技大学，2007.

[4] ELNOUBI S M. Analysis of GMSK with Two-Bit Differential Detection in Land Mobile Radio Channels[J]. IEEE Transactions On Communications,1987,35(02): 237-240.

[5] HEINZ M. Differential Detection of GMSK Signals with Low BT Using the SOVA[J]. IEEE Transaction on Communication, 1998,46(04): 428-430.

[6] KORN I. Binary PR CPM with Differential Phase Detection and Maximal Ratio Combining Diversity in Fading Channels[J]. IEEE Trans. V T, 1998,47(03):936-946.

[7] 彭伟智,李小文. TD—SCDMA系统中Viterbi算法研究与改进[J]. 通信技术, 2007, 40(11):105-106.

[8] BERNARD S. Digital Communications Fundamentals and Applications[M]. 北京：电子工业出版社，2002:307-313.