双馈电机转子绕组匝间短路电磁力计算

李俊卿，王喜梅

(华北电力大学 电气与电子工程学院，河北 保定 071003)

0 引言

双馈发电机作为风机系统中的关键设备之一，转子绕组匝间短路是发电机电气故障之一[1～3]，当发电机转子绕组发生短路故障时，将会缩短故障线圈及周围绝缘的寿命，而且电机本身受到很大的冲击电磁力及电磁力波，会使电机产生极大地电磁噪声级破坏性振动，进而引发一系列问题。因此，对电机故障运行电磁力分布进行准确地计算具有很大的价值。

常见的分析方法有不平衡电流法、负序分量法、坐标变换法[4]、瞬态功率法等。有限元法(FEM)是工程领域应用广泛的一种仿真技术[5～7]。文献[6]基于有限元法研究了感应电机匝间短路，并对电流和转矩进行了频谱分析。文献[8]通过改变模型的的线圈匝数来模拟永磁发电机定子绕组匝间短路，进行电磁场分析。

对电机电磁力的计算国内外做了大量的研究。文献[8]基于麦克斯韦应力法对汽轮发电机转子表面电磁力分布进行了计算。文献[9]对局部虚位移法进行改进，得到了电机电磁力密度的分布。电机中，磁通产生切向力和轴向力，引起切向振动和轴向振动，但主要是径向的。要分析和控制这些噪声，必须知道它们的来源，即产生振动和噪声的力波。本文以有限元法为基础建立双馈电机电磁力计算模型。计算双馈电机正常和转子匝间短路时的电磁力波分布。

1 建模

1.1 电机建模的假设条件

忽略电机端部效应和磁滞效应;不考虑涡流损耗和集肤效应。采用矢量磁位Az建立发电机二维电磁场数学模型:

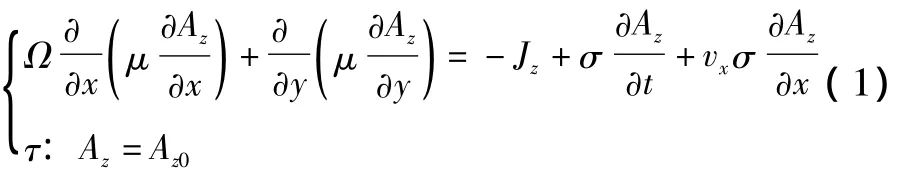
式中:vx为转速x方向上的分量;Jz为源电流密度z方向上的分量;μ为磁导率;σ为电导率;Az0为边界τ上Az的已知值，由于电机内铁磁物质的磁导率远远大于空气磁导率，可认为磁力线与边界平行，满足第一类 (狄利克雷)边界条件，取Az=Az0=0。即电机外部磁场忽略不计，定子外表面圆周为零矢量位面。

1.2 电磁力的计算

电磁力波由电机气隙磁场产生，作用于定子铁心内表面积上的电磁力是时间和空间的函数。电磁力的计算比较普遍的一种方法是电磁力的能量计算法，先计算气隙空间的磁场能量，然后将此对x，y进行求导，直接得到作用于转子外圆周沿x，y的电磁力Fx，Fy。另一种是根据麦克斯韦应力张量法，本文采用麦克斯韦应力法。可以得出作用在电机定子转子切向力(t)和法向力(n)电磁力密度为

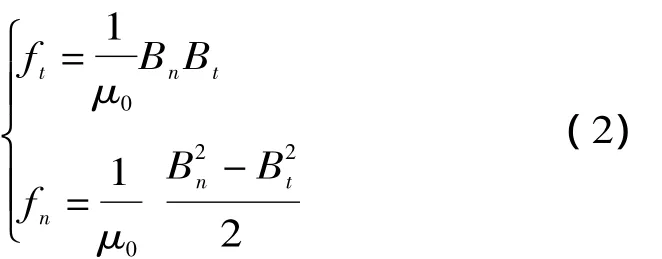
对电磁力波沿气隙进行进行积分，离散后的电磁力:

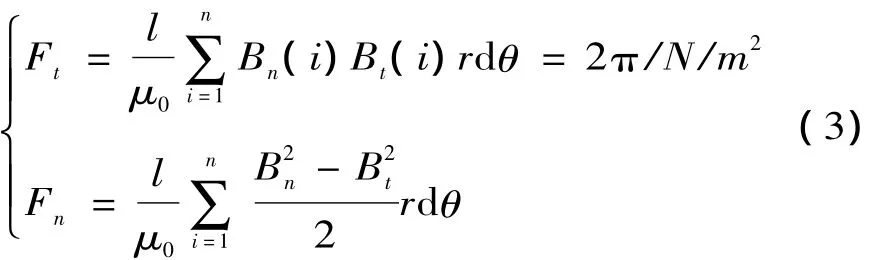
式中:Bn(i)和Bt(i)分别为气隙第i个单元磁通密度的切向和径向分量;r为各个气隙单元的旋转半径;n为气隙带圆周上的总单元数;dθ=2π/n为每个单元所占机械角度;l为电机铁心的轴向长度。

可以得出作用在电机定子转子水平(x)和垂直方向(y)电磁力密度为

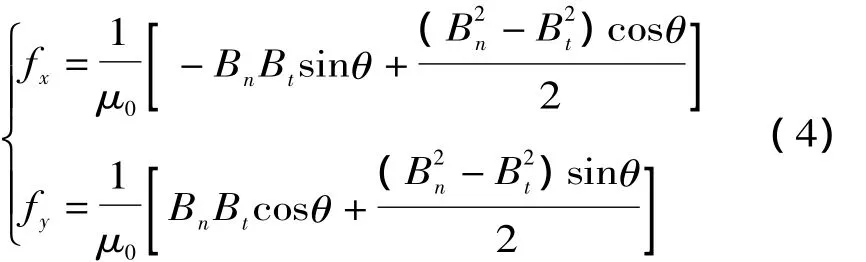
对电磁力波沿气隙进行进行积分，离散后的电磁力:

本文中电机的基本参数如下:额定功率为5.5 kW;极对数为2;定、转子槽数为36/24，每槽线数为74/24;定子三相绕组为三角形联结，并联支路数为2，节距为1～9，定子外径为210 mm，内径为136 mm;转子三相绕组为星型联结，并联支路数为1，节距为1～6，转子外径为135.2 mm，内径为48 mm，气隙为0.4 mm，铁心长度为16 mm。

2 仿真结果及分析

双馈式发电机运行时电机转速与定、转子绕组电流频率关系的数学表达式:式中:取“－”号时，双馈式风力发电机运行在亚同步速状态;取“+”时，双馈式风力发电机运行在超同步速状态。f1为定子绕组电流频率;f2为馈入转子绕组的电流频率;p电机极对数;n为电机转子转速。

2.1 电机电磁场分布

电机选取整个电机圆周为计算区域。双馈电机激励由转子侧加载，认为气隙磁场仅由转子磁势产生，定子绕组开路，定子侧电流为0。仿真双馈电机在亚同步状态下正常，转子a相绕组2匝短路以及5匝短路的情况。设置电机转速为1 200 r/min，转子施加的频率为10 Hz。得到电机磁力线分布如图1所示。

从图1(上)可以看出，当电机未发生短路故障时，电机内磁场分布均匀，三相对称绕组产生的磁场对称性良好。当电机转子绕组发生2匝短路时 (图1(中))，只有故障绕组对应磁极的磁力线发生了变化偏移，和中心对称的位置的磁力线不再是对称的，其余位置变化不大。当短路匝数增加到5匝时 (图1(下))，电机相应4个磁极均不再对称。显然，此时电机磁场较正常时已发生了很大变化。总体来说，发电机转子绕组发生匝间短路故障后，各故障绕组附近磁场加深，随着故障严重程度的增长而变化。电机其余位置在故障初期变化不明显，但当短路匝数增加至一定程度时会受到较大影响。

2.2 电机电磁力波分析

由电磁力的能量计算法，得到电磁力Fx，Fy如图2所示。图中，横轴表示定、转子空间位置;纵轴代表切向电磁力波值，单位为kN。

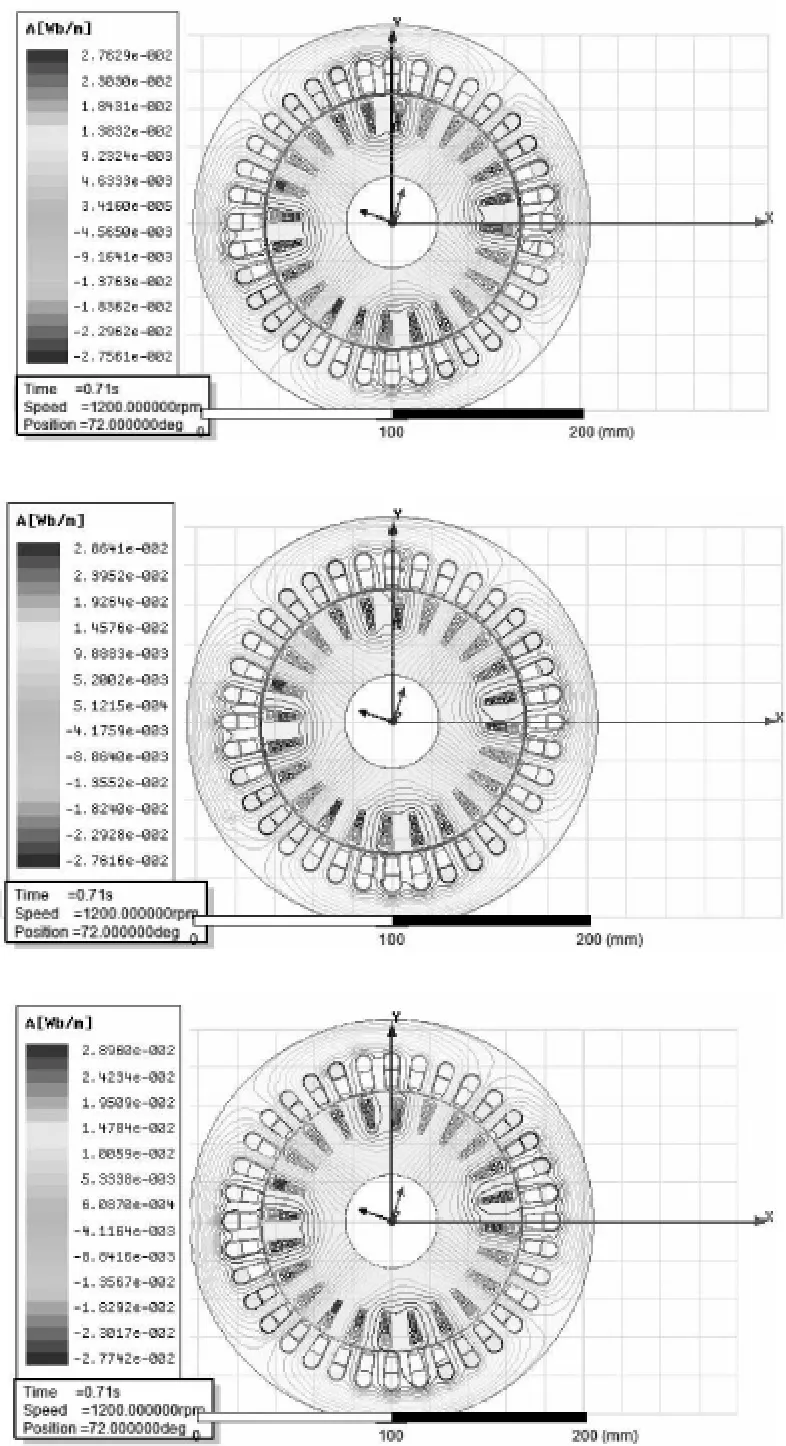
图1 正常，a相短路2匝和5匝时的电机内磁力线分布Fig.1 Magnetic field lines distribution:healthy，2 turns inter-turn short-circuit，5 turns inter-turn short-circuit

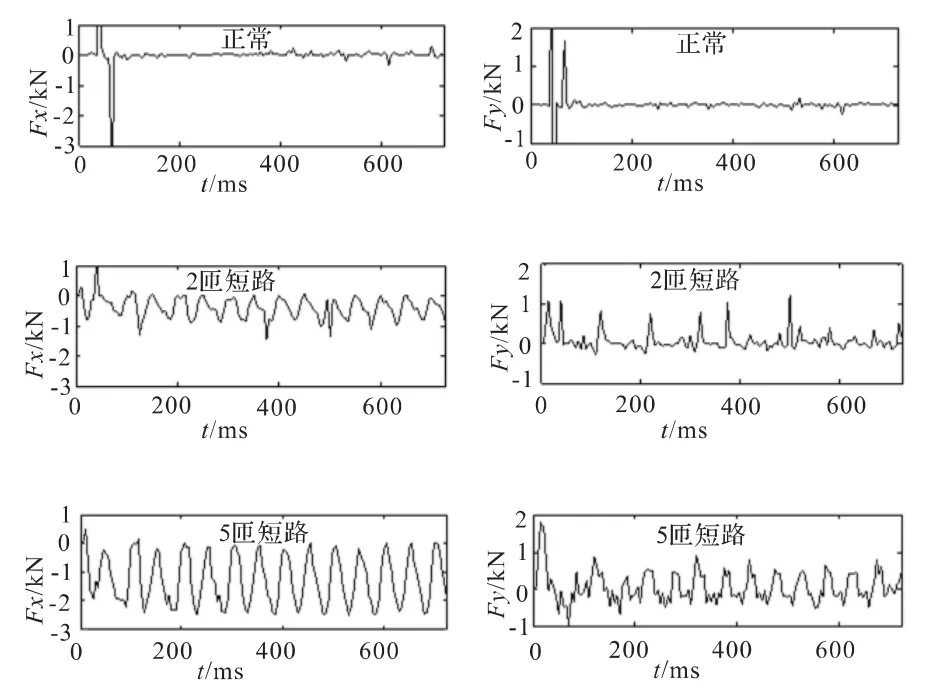
图2 电机x，y方向电磁力Fig.2 x，y direction electromagnetic force of DFIG

可以看出，正常情况下，电机在xy方向产生的电磁力很小，因为此时电机内电磁场是均匀对称分布的，当发生故障时，xy方向受力将不再对称，相应地总的合成的电磁力也变得很大，而且随着绕组短路匝数的增大而增大。从短路故障下xy方向气隙磁场所产生的电磁力，尤其是短路5匝x方向产生的电磁力，可以明显看出电磁力0.1 s内变化两个周期，电机为两对极的，所以电磁力中10 Hz的含量增大，此时转子电流的频率是10 Hz。由此看出，电磁力和转子电流的频率相关，在电机水平和垂直方向，转子电流频率对应的振动明显。

按照麦克斯韦向量法得到电机切向电磁力波分布如图3，4所示，径向电磁力波分布如图5所示。图中，横轴表示定转子空间位置;纵轴代表切向电磁力波值，单位为N/m2。

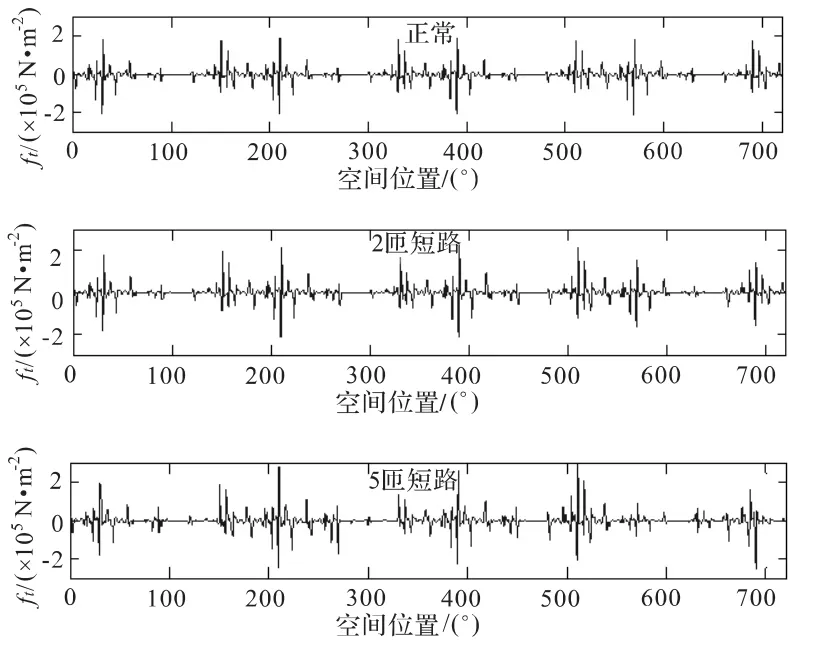
图3 电机切向电磁力波分布Fig.3 Distribution of DFIG tangential electromagnetic force wave

图4 电机切向电磁波分布局部放大图Fig.4 Partial enlarged view of DFIG tangential electromagnetic force wave distribution

可以看出，正常情况下相对均匀些。电机所受切向力的最大值正常，2匝、5匝分别为184 696 N/m2，212 788 N/m2和 293 686 N/m2。将3种情况进行比较，局部放大后如图4所示，波形变化不是很大，但是随着故障程度的增加趋势是一样的。

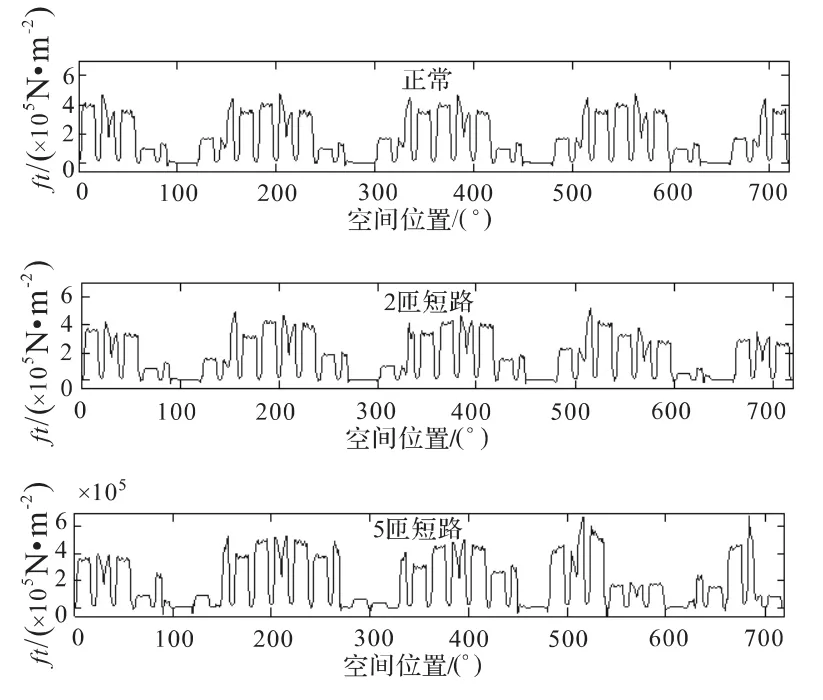
图5 电机径向电磁力波分布Fig.5 Distribution of DFIG radial electromagnetic force wave

通过对正常以及不同故障程度下的电机气隙磁密波形图 (图5)进行观察可知:转子绕组匝间短路故障对于电磁力波的影响主要体现为空间分布的影响。首先，随着故障程度的增加，最大的径向电磁力波值增大，最大值分别为471 152 N/m2，518 508 N/m2，和 679 670 N/m2。同时出现的负值逐渐减小，分别为 －22 082 N/m2，－22 570 N/m2和 －61 031 N/m2。其次，当故障未发生时，4个极是对称的，并呈现良好对称性。当短路匝数增加到5匝时，波形发生较明显变化，失去了原有的电机内空间对称性，受力不均匀。主要是匝间短路引起电流不平衡，特别是故障绕组对应空间位置的气隙磁通发生很大的改变，从而气隙磁密不均匀，进而使受到的电磁力将不再均匀。

2.3 电机径向电磁力波的分析

由于气隙引起的噪声主要是径向的，所以对电机径向电磁力波进行进一步分析。电磁力波由气隙磁场得出，气隙磁场在不同时刻，考虑到齿槽效应，严格来讲是有变化的。当然，如果忽略了齿槽效应，那么基波磁场幅值就与时间无关了。所以选取一个周期 (0.02 s)的径向电磁力波的最大值进行比较，数据如表1所示。进行频谱分析，得到的径向电磁力波的频谱分布如图6所示。

由表1可以看出电磁力波最大值点随着故障程度增加而增大，并且上下浮动的值增大，电机受力不均匀而且增大可能导致绝缘损坏，这种情况如果不及时得到解决，将会导致电磁转矩脉动程度增加，对电机稳定运行造成威胁。

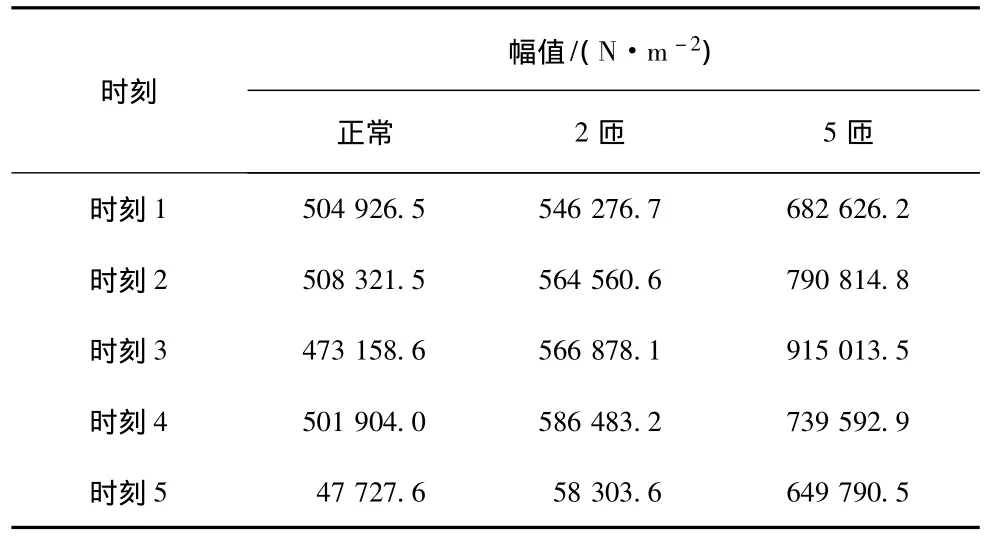
表1 一个周期内径向电磁力波最大值Tab.1 Maximum radial electromagnetic force wave in a cycle

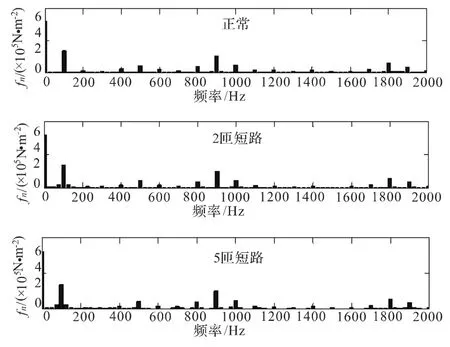
图6 径向电磁力波的频谱分布Fig.6 Spectrum distribution of radial electromagnetic force wave

正常情况下的径向电磁力波频谱图中可以观察到:除了基波，含有一定的2次谐波分量和一定量的高次谐波分量，如20，40次谐波分量，考虑到齿槽谐波，是和相应的气隙磁密对应的。频谱中基本不存在明显的分数次和奇数次谐波分量。当出现匝间故障时，径向电磁力波的频谱变得复杂，随着故障程度的增加，分数次谐波逐渐增大。

根据振型特性，相对于低阶脉振电磁力，电机受高阶电磁力波作用变形时相邻节点间距离小，刚度较大，而振幅较小，所以一般只考虑振幅较大的低阶脉振电磁力。选取一个周期内的电磁力波200 Hz以下的幅值数据 (如表2～6所示)，进行分析。

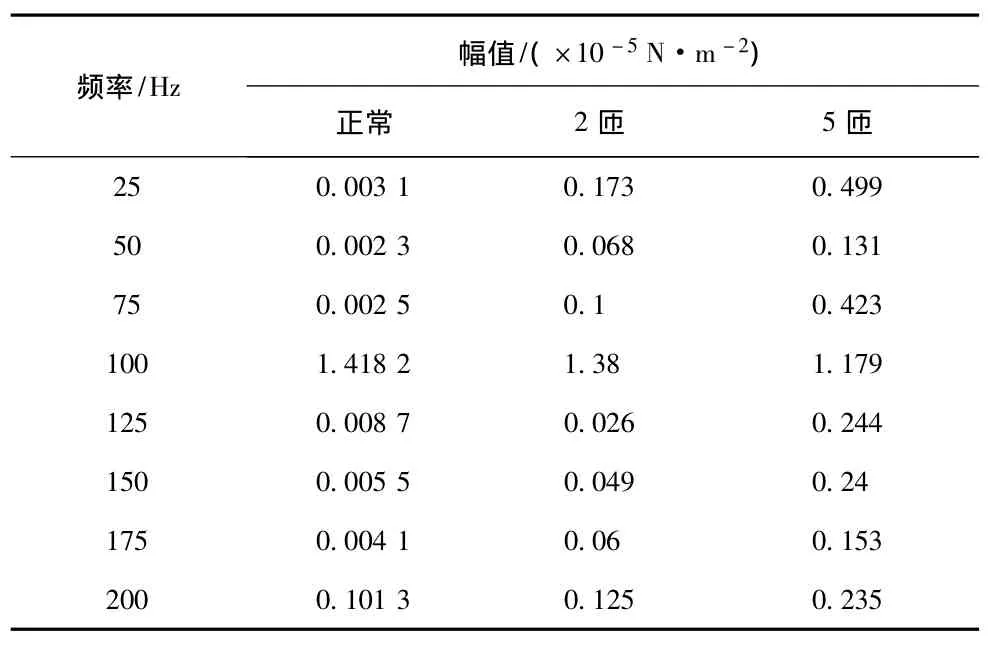
表2 径向电磁力波各次谐波幅值 (时刻1)Tab.2 Harmonic amplitude of radial electromagnetic force wave(at moment 1)

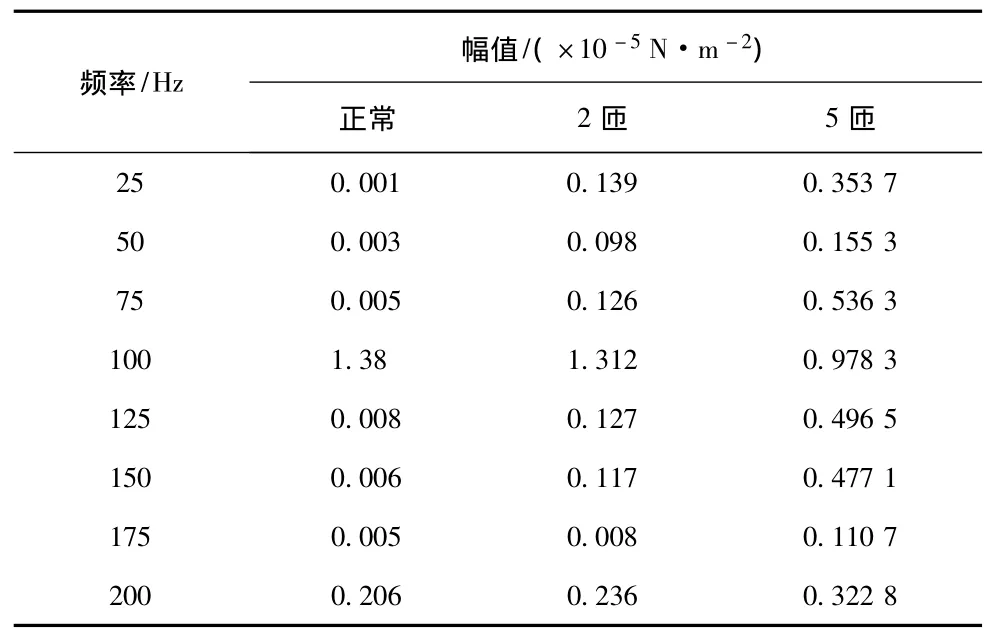
表3 径向电磁力波各次谐波幅值 (时刻2)Tab.3 Harmonic amplitude of radial electromagnetic force wave(at moment 2)

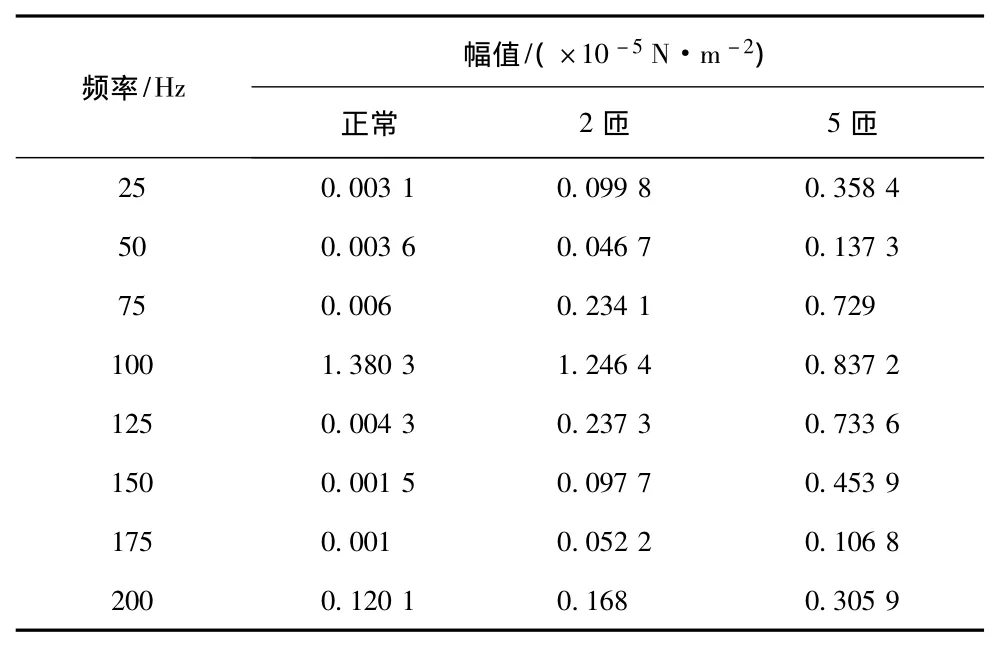
表4 径向电磁力波各次谐波幅值 (时刻3)Tab.4 Harmonic amplitude of radial electromagnetic force wave(at moment 3)

由表2到表6可以清楚地看到，50 Hz和150 Hz奇数次谐波含量是明显增加的。分数次谐波的含量也是逐渐增大的。偶数次谐波含量的幅值变化还在同一个数量级里面，相对变化不是很大，而且100 Hz和200 Hz变化规律是相反的。

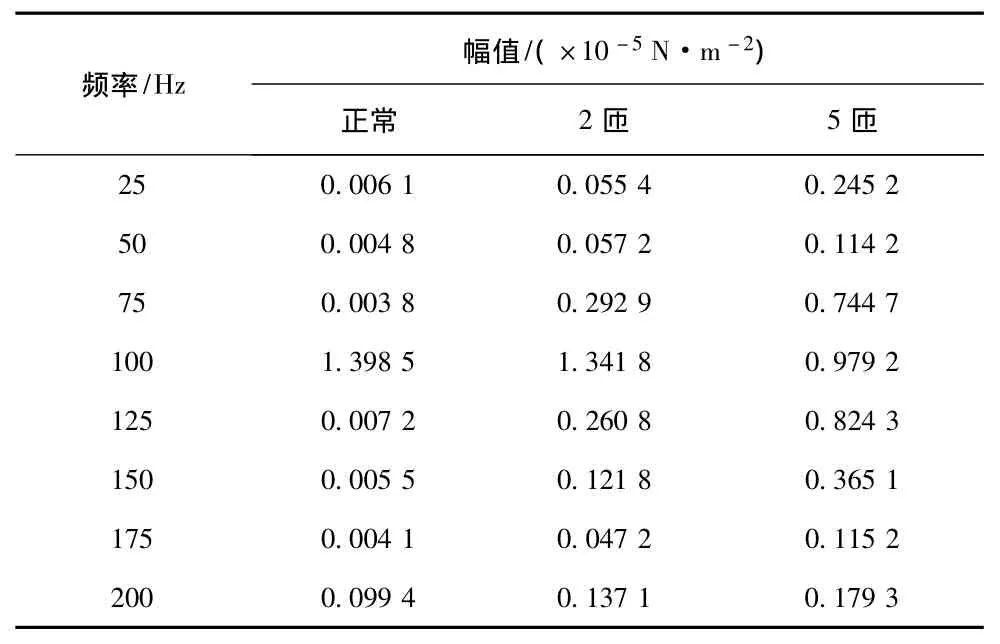
表5 径向电磁力波各次谐波幅值 (时刻4)Tab.5 Harmonic amplitude of radial electromagnetic force wave(at moment 4)

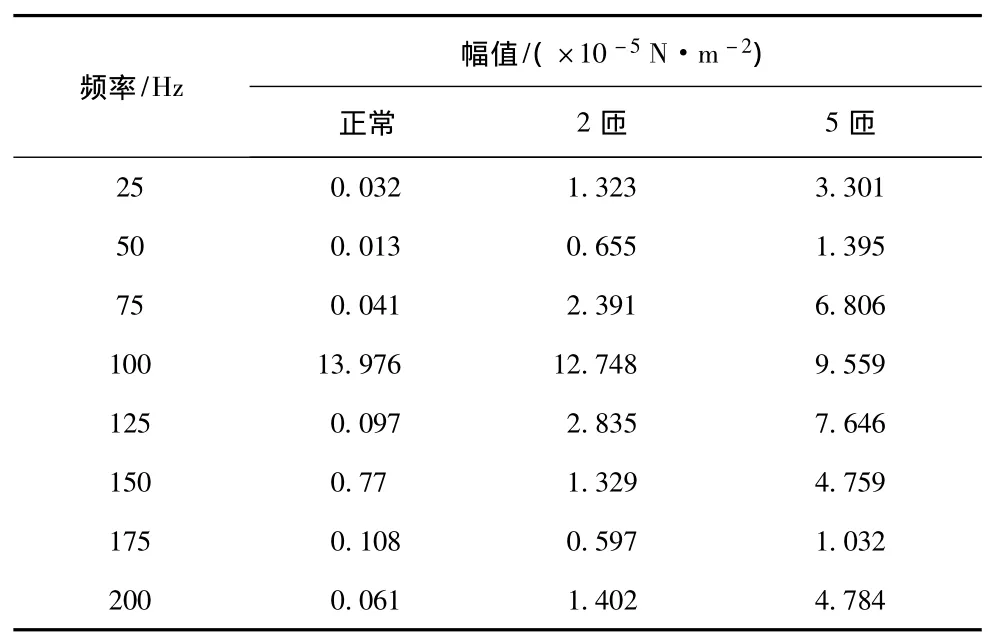
表6 径向电磁力波各次谐波幅值 (时刻5)Tab.6 Harmonic amplitude of radial electromagnetic force wave(at moment 5)

3 结论

本文建立了双馈电机的有限元仿真模型，并分析了电机在正常和转子绕组故障下的磁力线分布;运用麦克斯韦应力法计算由气隙磁场产生的xy方向的电磁力;电机的切向和径向电磁力波;并对径向电磁力波进行频谱分析。可以看出:(1)当双馈电机发生转子绕组匝间短路时，电机电磁场将不再均匀，随着故障程度的增加，磁力线偏移增大。(2)气隙磁密产生的电磁噪声将变得复杂。引起振动的电磁力波的振动频率变得多一些，并且出现了许多的分数次谐波。振动的激振力在50 Hz和150 Hz时增大明显。(3)故障后整体受力不均匀，产生的xy方向的电磁力，径向和切向电磁力波的最大值随着故障程度的增加而增大。双馈电机发生转子绕组故障达到稳态运行时，整个磁场相对来说是固定的，对双馈电机超同步和亚同步状态进行分析得到的xy方向的电磁力变化规律是一致的。