配置HRBF500钢筋的无粘结预应力梁受弯性能试验研究

郑毅敏，何礼东，赵 勇

（同济大学a.建筑设计研究院（集团）有限公司；b.建筑工程系，上海200092）

采用500 MPa级钢筋代替335或400 MPa级钢筋作为混凝土梁的受拉纵筋后，在同样的受弯承载力要求下，一般可以减少钢筋的用量，具有较好的效益，值得推广应用。在新版中国国家标准《混凝土结构设计规范》［1］（GB 50010－2010）中已将 HRB500和HRBF500钢筋纳入，而且已有的试验研究结果表明［2－4］，规范 GB 50010－2010的正截面受弯承载力计算公式适用于配置500 MPa级钢筋的非预应力混凝土梁。由于规范GB 50010－2010中无粘结预应力梁的受弯承载力计算模式主要源自行业标准《无粘结预应力混凝土结构技术规程》［5］（JGJ 92－2004），且是建立在配置335 MPa级钢筋的梁、板受弯性能试验结果的基础上的，是否仍适用于配置500 MPa级钢筋的无粘结预应力梁值得商榷。

1 试验方案

1.1 试件基本情况

试验共设计了8根无粘结预应力梁和2根非预应力梁，所配置的纵向非预应力受拉钢筋均为HRBF500钢筋，且主要考虑了预应力筋合力点位置ap、综合配筋指标ξp和预应力筋分布形式等参数。试验梁的横截面为矩形，截面的宽b、高h分别为250、450 mm（图1），跨度为4 500 mm（净跨l0为4 200 mm）。试验梁中所配置的预应力筋为1 860级Øs15.2低松弛无粘结钢绞线，纯弯段的预应力筋线形均为直线。试验梁的基本情况见表1，表中f′cu为与试件同条件养护的立方体试块抗压强度，σpe为实测预应力筋有效预应力，λ和ξp分别为预应力强度比和综合配筋指标，按式（1）和（2）计算。

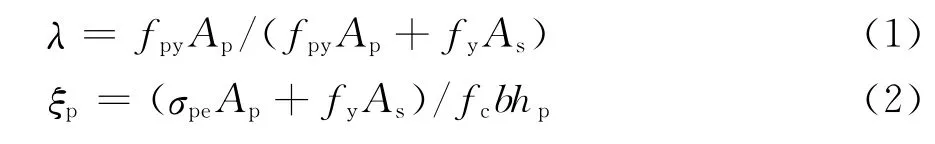
式中：fpy为预应力筋抗拉强度；Ap为预应力筋的面积；fy为非预应力筋抗拉强度；As为非预应力筋的面积；fc为混凝土轴心抗压强度；hp为预应力筋合力点至受压区顶面的距离。计算λ和ξp时，fc取0.76f′cu，fy取钢筋实测屈服强度。

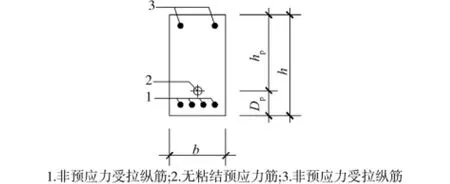
图1 试验梁跨中截面

试验梁均为简支梁，并分2批进行试验，其中第1批梁纯弯段长度为2 100 mm，其间未配有箍筋；第2批梁纯弯段长度为1 800 mm，其间配有箍筋φ12＠300。

1.2 加载方式

试验采用2点集中方式加载，其中第1批试验梁采用反向加载，第2批试验梁采用正向加载，加载简图见图2，图中P为千斤顶作用力。在非预应力受拉纵筋屈服前，采用力控制分级加载，在试验梁开裂之前，每级加载增量为10 k N；在试验梁开裂之后，每级加载增量提高为30 k N。当非预应力受拉纵筋屈服之后，缓慢加载直至试验梁破坏。

表1 试验梁基本情况

图2 加载简图

1.3 量测内容及方法

试验过程中量测的内容及方法为：1）采用压力传感器量测每根无粘结预应力筋两端的压力。2）采用电子位移计量测梁的挠度，测点布置在梁两端及跨中。3）采用钢筋应变片测量非预应力筋的应变εs，每根梁选择2根钢筋各布置2个钢筋应变片，测点布置在距离梁中线各200 mm的位置处。

2 主要试验结果

2.1 破坏特征

对于无粘结预应力混凝土试验梁，当荷载加至0.3Pu（Pu为试验梁的极限荷载）左右时，用肉眼可在试验梁纯弯段的底面及两侧表面发现一条或多条裂缝，裂缝宽度均很小，侧表面的裂缝高度一般可达梁高的1／4。随着荷载进一步增加，纯弯段裂缝逐渐增多，宽度也逐渐加大，且斜裂缝开始出现。当荷载增至0.6Pu左右时，裂缝基本出齐。当荷载达到极限荷载Pu后，跨中区域裂缝迅速变宽，破坏较为突然，破坏时跨中受压区边缘混凝土严重压碎，且第一批未配置箍筋的试验梁的受压钢筋有明显压屈现象（图3）。

图3 无粘结预应力梁的破坏特征

2.2 跨中的弯矩与挠度

各试验梁跨中的弯矩M与挠度f的关系曲线如图4所示。由图4可看出：1）在达到极限状态之前，M－f曲线仍大致呈3段折线，但与非预应力梁相比，无粘结预应力梁的第3段折线明显偏短，且梁达到极限状态后的下降段较陡。2）与第2批梁比较，第1批梁的曲线的下降段更加陡，破坏更为突然。

无粘结预应力试验梁M－f曲线的第1个转折点处相应的弯矩Mf1约为极限弯矩的30%～40%，第2个转折点处相应的弯矩Mf2约为极限弯矩的87%～98%，而由文献［6］可知，配置335 MPa级钢筋的无粘结预应力梁的Mf1、Mf2与极限弯矩之比分别为19%～29%、58%～98%，均比试验结果偏小。

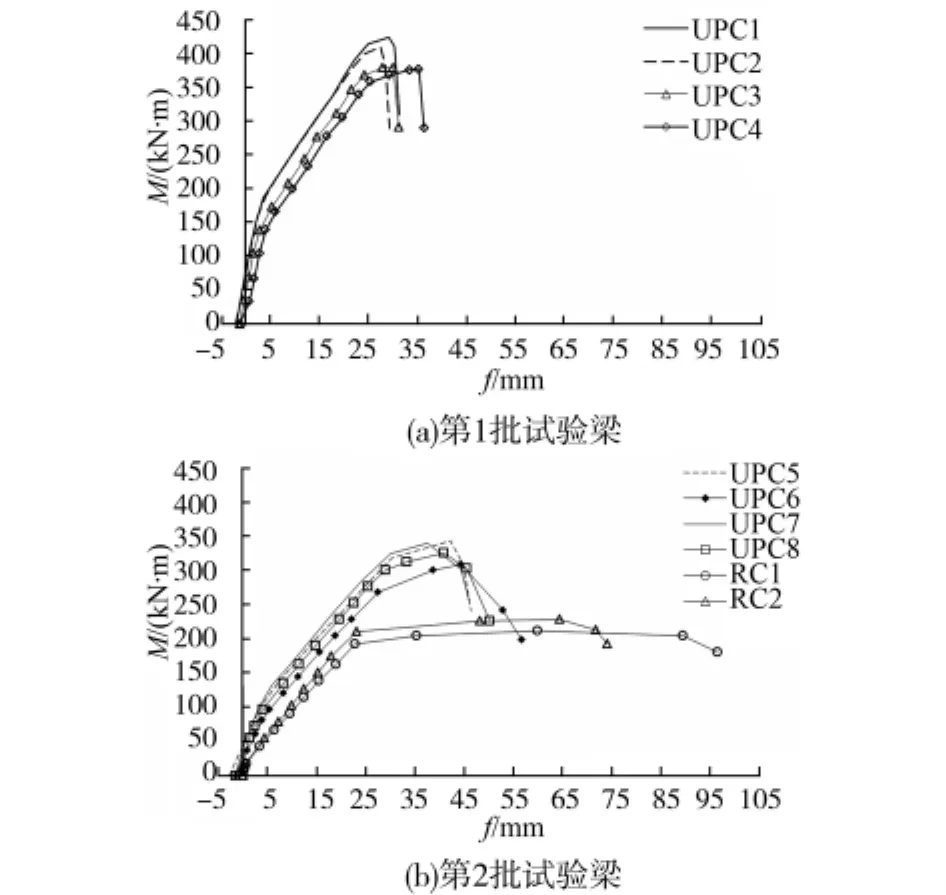
图4 试验梁跨中的弯矩与挠度关系

2.3 跨中弯矩与预应力筋应力增量

各试验梁跨中弯矩M与无粘结预应力筋应力增量Δσp的关系曲线如图5所示，其中预应力增量取为各压力传感器测试结果的平均值，由于采用人工读数，部分试件未能采到极限预应力值。由图5可看出：1）在达到极限荷载之前，除试验梁UPC1和UPC2的M－Δσp曲线大致呈2段折线外，其他试验梁的M－Δσp曲线大致呈3段折线。2）对比试验梁UPC2和 UPC1、UPC4和 UPC3、UPC6和 UPC5、UPC8和UPC7可知，当预应力筋布置形式相同时，随着ξp增大，Δσpu的增长速率减小。3）对比试验梁UPC5和UPC7、UPC6和UPC8可知，当ξp相同时，预应力筋布置形式对Δσpu的增长速率影响不明显。

文献［6－13］中试验梁的极限预应力增量Δσpu与ξp的关系如图6（a）所示，可以看出，当ξp≤0.30时，Δσpu与ξp基本成线性关系，但当ξp＞0.30时，二者的线性关系不明显。试验的无粘结预应力梁的ξp为0.34～0.43，Δσpu与ξp的关系如图6（b）所示，可见，对于配置HRBF500钢筋的无粘结预应力混凝土梁，Δσpu与ξp仍基本成线性关系，且随ξp增大，Δσpu减小。

2.4 跨中弯矩与受拉非预应力钢筋应变

各试验梁的跨中弯矩M与非预应力钢筋应变εs关系曲线如图7所示，其中εs为裂缝附近测点的钢筋应变值。由图7可见：1）在达到极限荷载之前，试验梁的M－εs曲线基本呈2段或3段折线。2）在试验梁达到极限状态之前，受拉的HRBF500钢筋均已屈服，即在无粘结预应力梁中，HRBF500级钢筋的强度能够充分发挥。

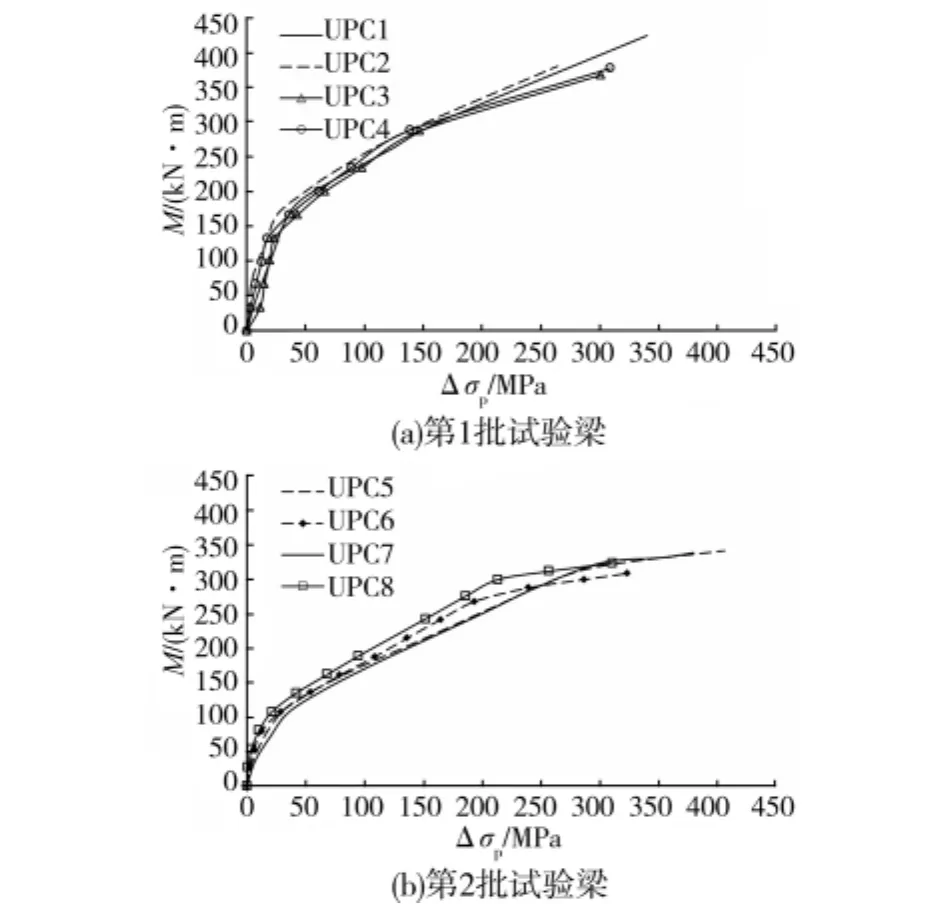
图5 试验梁跨中弯矩与预应力筋预应力增量关系

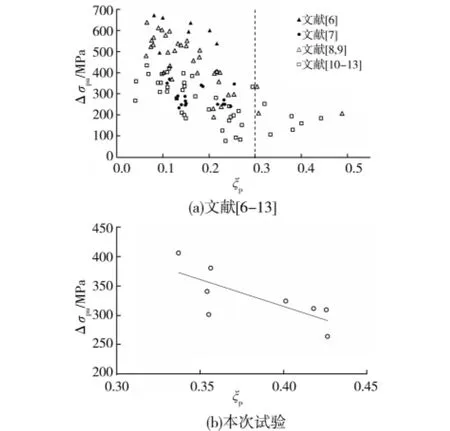
图6 试验梁极限预应力增量与综合配筋指标关系

3 试验结果分析

3.1 承载力结果分析

3.1.1 M、f、Δεp、εs之间的关系 对无粘结预应力试验梁的 M－f、M－Δεp、M－εs曲线进行对比后可知（图8）：1）在达到极限状态之前，M－εs曲线首先达到第1个转折点，其次是M－Δεp曲线，最后是M－f曲线，即梁出现裂缝后，首先直接影响到的是非预应力筋的应力值，然后影响到预应力筋应力值，而跨中挠度值的增量需要裂缝进一步发展后才会出现改变。2）当非预应力筋达到屈服应变时，M－f 曲线和M－Δεp曲线均未达到第2个转折点。

图7 跨中弯矩与非预应力受拉筋应变关系

图8 无粘结预应力梁M、f、Δεp、εs之间的关系

3.1.2 承载力影响因素分析 各试验梁的跨中实测极限弯矩Mu与相关参数ap、ξp及预应力筋布置形式见表2。由表可知：1）比较试验梁UPC1和UPC2、UPC3和 UPC4、UPC5和 UPC6、UPC7和UPC8可知，当预应力筋布置形式相同时，随着ξp增大，Mu减小。2）比较试验梁UPC1和UPC3、UPC2和UPC4、UPC8和UPC6可知，当ap相同时，预应力筋分散布置会使Mu降低。

表2 试验梁的极限弯矩与相关参数

3.2 延性分析

采用跨中位移延性系数μΔ作为梁的延性评价指标，且位移延性系数μΔ按式（3）计算。

式中：Δu为M－f曲线下降段上取85%极限弯矩对应的跨中位移；Δy为非预应力受拉纵筋屈服时对应的跨中位移，非预应力受拉纵筋屈服根据M－εs曲线判定。

根据式（3）计算的试验梁位移延性系数见表3。由表3可知：1）无粘结预应力试验梁UPC1～UPC8的位移延性系数为1.30～1.99，平均为1.67，非预应力试验梁RC1、RC2的位移延性系数分别为4.68、3.43，平均为4.05，即与非预应力梁相比，预应力梁的位移延性系数明显偏小；2）当预应力筋布置形式相同时，影响无粘结预应力筋混凝土梁位移延性的主要因素为综合配筋指标ξp，随着ξp增大，位移延性系数减小。

然而，文献［14］中的无粘结预应力试验梁的位移延性系数为2.30～9.00，相应的非预应力筋屈服强度为265.0～477.5 MPa，ξp为0.08～0.23，位移延性系数明显大于本次试验梁的结果。由此可见，对于配置500 MPa级钢筋的无粘结预应力梁，由于钢筋的屈服强度增大，相应的Δy也增大，导致位移延性系数减小。

4 承载力计算方法

4.1 受弯承载力计算方法

下按平截面假定建立的，因此，确定无粘结预应力混凝土梁的受弯承载力Mu的关键是确定Δσpu。

式中：Δσpu为无粘结预应力筋的极限预应力增量，为与混凝土强度等级有关的计算系数；x为受压区高度。

4.2 极限预应力增量计算方法

根据规范GB 50010－2010，矩形截面单筋正截面受弯承载力可按式（4）计算。式（4）是在已知Δσpu

极限预应力增量Δσpu是无粘结预应力梁受弯性能的一个重要指标，国内外学者已对其进行了大量的研究，提出了各种计算方法，而且相关标准也给出了Δσpu的计算规定，但这些Δσpu计算公式形式多样，未能统一。结合笔者及相关文献中的试验结果，对中国规范GB 50010－2010和美国规范ACI 318－08［15］进行评估，并经回归分析得到了 Δσpu的建议公式。

对于单跨梁，中国规范GB 50010－2010的无粘结预应力筋的极限应力增量（记为Δσcp1u）的计算公式为式（5）。

式中h为受弯截面高度。

对于跨高比小于等于35的梁，美国规范ACI 318－08［15］的无粘结预应力筋的极限应力增量（记为）计算公式为式（6）。

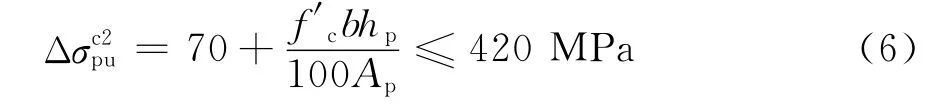
式中f′c为混凝土圆柱抗压强度标准值（当混凝土强度等级小于C50时，取

表3 试验梁的位移延性系数

本次试验梁的极限预应力增量的试验值与按中、美规范的计算值见表4，表中为预应力增量的试验值。由表4可知，本次试验梁的极限应力增量试验值比中、美规范的计算值明显偏大，的平均值和变异系数分别为0.35和0.095的平均值和变异系数分别为0.39和0.090。

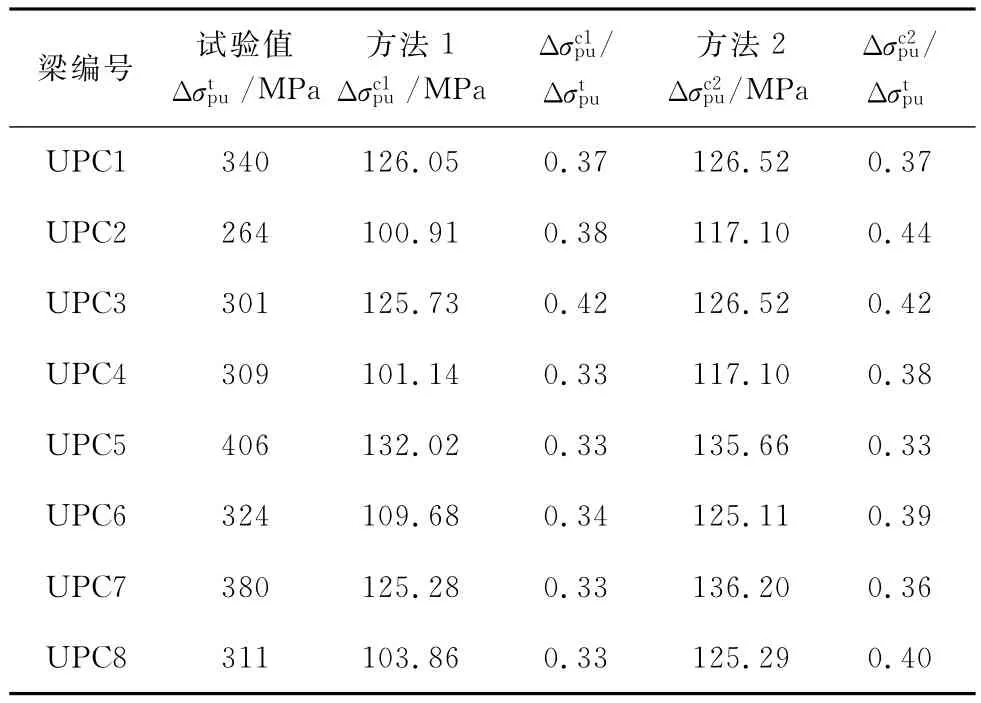
表4 极限应力增量试验值与规范计算值比较

笔者及文献［6－13］的试验结果与中、美规范中公式的计算结果比较见图9。由图9可看出，试验梁的极限应力增量试验值比中、美规范中公式的计算值大，且试验值越大，偏差越大，同时总体来看计算值与试验值二者离散度较大，的平均值和变异系数分别为0.61和0.501的平均值和变异系数分别为0.68和0.456。

为了得到与试验结果较吻合的计算公式，参考文献［16］的研究成果，建立了如式（7）所示的无粘结预应力梁预应力增量（记为）计算公式。按式（7）的计算值与试验值的比较见图10，其比值平均值为0.99，变异系数为0.490，当极限预应力增量试验值小于450 MPa时，二者符合较好。

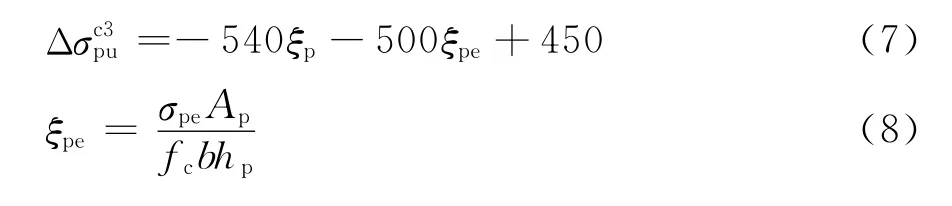
4.3 承载力计算结果

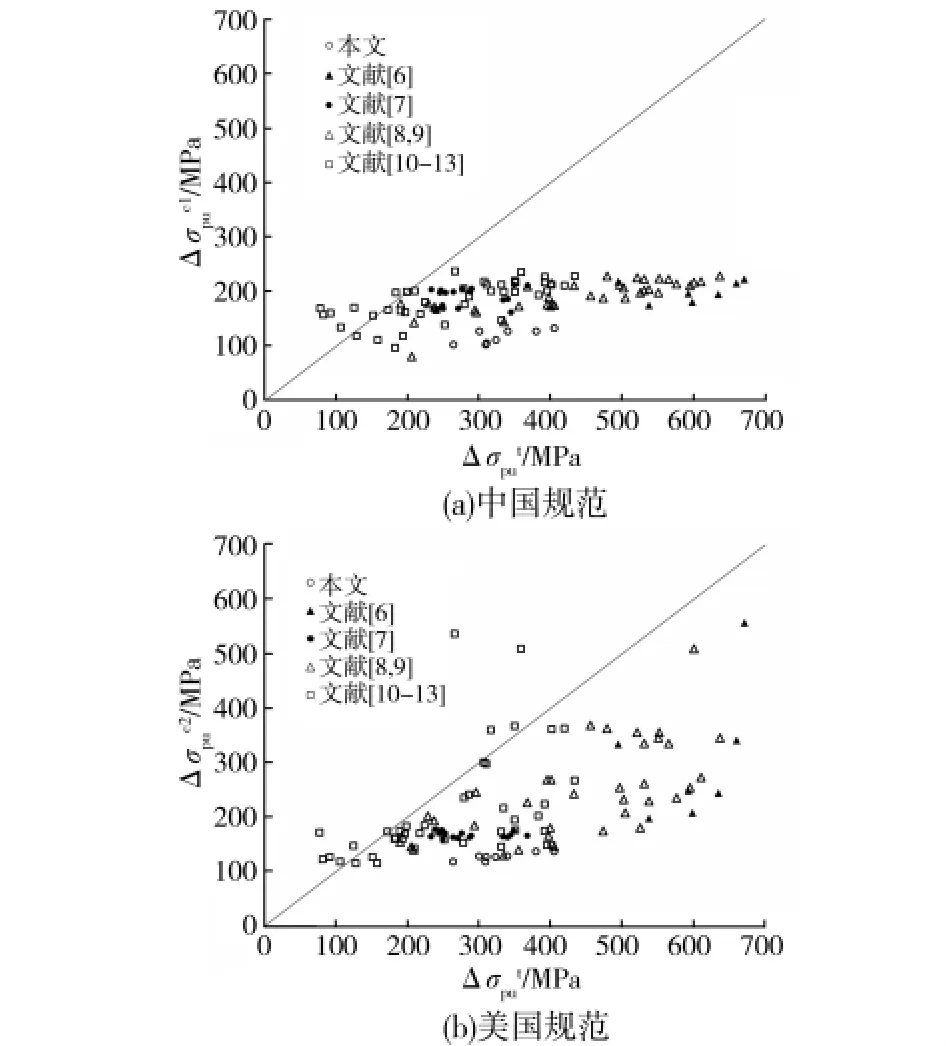
图9 极限应力增量试验值与规范计算值比较

图10 极限应力增量建议公式计算值与试验值比较

表5 受弯承载力计算值与试验值比较

5 结 论

通过试验研究及与相关文献试验结果对比，对配置HRBF500钢筋的无粘结预应力混凝土梁的受弯承载力性能，可以得到以下结论：

1）在达到极限状态之前，试验梁M－f曲线仍大致呈三折线，且非预应力受拉纵筋均能屈服，但梁的破坏较为突然。

2）试验梁的极限预应力增量Δσpu试验值与综合配筋指标仍基本成线性关系，而且随ξp增大，Δσpu减小的试验值与按中国规范GB 50010－2010和美国规范ACI 318－08中公式的计算值明显偏大。

3）根据笔者及相关文献中的试验结果，分析得到了Δσpu的计算建议公式，当Δσpu试验值小于450 MPa时，该式的计算值与试验值符合较好。

4）无粘结预应力试验梁的跨中位移延性系数均较小，平均为1.67，且随ξp的增大而减小。以延性为目标的极限预应力增量取值有待进一步研究。

［1］GB 50010－2010混凝土结构设计规范［S］.北京：中国建筑工业出版社，2010.

［2］王铁成，李艳艳，戎贤.配置500 MPa钢筋的混凝土梁受弯性能试验［J］.天津大学学报，2007，40（5）：507－511.WANG Tiecheng，LI Yanyan，RONG Xian.Test f or bending behavior of reinforced concrete beam with 500 MPa steel bar［J］.Journal of Tianjin University，2007，40（5）：507－511.

［3］李志华，苏小卒，赵勇.配置500 MPa钢筋的混凝土梁受弯性能试验研究［J］.南昌大学学报：工科版，2010，32（1）：40－44.LI Zhihua，SU Xiaozu，ZHAO Yong.Experi mental research on flexural behavior of reinf orce concrete beams with 500 MPa steel bars ［J］.Jour nal of Nanchang University：Engineering＆Technology，2010，32（1）：40－44.

［4］赵进阶.配HRBF500级钢筋混凝土梁受弯性能试验研究［D］.北京：北京工业大学，2008.

［5］JGJ 92－2004无粘结预应力混凝土结构技术规程［S］.北京：中国建筑工业出版社，2005.

［6］宋永发，王清湘.无粘结部分预应力高强混凝土梁正截面承载力计算［J］.大连理工大学学报，1996，36（2）：224－229.SONG Yongfa，WANG Qingxiang.Calculation of nor mal section strength of unbounded partially prestressed concrete beams with high strength concrete［J］.Jour nal of Dalian University of Technology，1996，36（2）：224－229.

［7］刘健行.无粘结部分预应力砼梁受弯承载力计算［J］.建筑结构学报，1992，13（6）：30－40.LIU Jianxing.Calculation of flexural capacity of unbounded partially prestrssed concrete beams［J］.Journal of Building Structures，1992，13（6）：30－40.

［8］杜拱辰，陶学康.部分预应力混凝土梁无粘结筋极限应力的研究［J］.建筑结构学报，1985，6（6）：2－13.DU Gongchen，TAO Xuekang.A study of the ulti mate stress of unbounded tendons in partially prestressed concrete beams ［J］.Jour nal of Building Str uct ures，1985，6（6）：2－13.

［9］王逸，杜拱辰，刘永颐.跨中集中荷载下部分预应力梁无粘结筋极限应力的研究［J］.建筑结构学报，1991，12（6）：42－52.WANG Yi，DU Gongchen，LIU Yongyi.Ulti mate stress in unbounded tendons of partially prestressed concrete beams under mid－span loading［J］.Jour nal of Building Str uct ures，1991，12（6）：42－52.

［10］Ta m A，Pannell F N.The ulti mate mo ment of resistance of unbonded partially prestressed reinforced concrete beams［J］.Magazine of Concrete Research，1976，28（97）：203－208.

［11］Mattock A H，Yamakazi J，Kattula B T.Co mparative st udy of prestressed concrete beams with and without bond［J］.ACI Jour nal，1971，68（2）：116－125.

［12］Campbell T I，Chouinar d K L.Influence of nonprestressed reinforcement on the strength of unbonded partially prestressed concrete members ［J］.ACI Str uctural Jour nal，1991，88（5）：546－551.

［13］Harajli M H，Kanj M Y.Ulti mate flexural strengt h of concrete members prestressed with unbonded tendons［J］.ACI Str uctural Jour nal，1991，88（6）：663－673.

［14］宋永发，宋玉普.无粘结部分预应力高强混凝土梁延性试验研究［J］.大连理工大学学报，2002，42（5）：586－589.SONG Yongfa，Song Yupu.Experi mental research on ductility of unbounded partially prestressed high strengt h concrete beams ［J］.Jour nal of Dalian University of Technology，2002，42（5）：586－589.

［15］ACI Committec 318.ACI 318－08.Building code requirements for structural concrete and commentary［S］.Michigan：American Concrete Institute，2008.

［16］郑文忠，王晓东，王英.无粘结筋极限应力增量计算公式对比分析［J］.哈尔滨工业大学学报，2009，41（10）：7－13.ZHENG Wenzhong，WANG Xiaodong，WANG Ying.Comparison of for mulas for calculating the ultimate stress increment in unbounded tendons［J］.Journal of Harbin Institute of Technology，2009，41（10）：7－13.