深水作业浮标系泊系统研究与设计
2012-08-11王小波韩端锋韩海辉
王小波 韩端锋 刘 峰 韩海辉
(哈尔滨工程大学 船舶工程学院 哈尔滨150001)
0 引 言
海洋环境资料浮标(简称“海洋浮标”)是一个无人的自动海洋观测站,其工作范围一般限定在某个海域,随波起伏,如同航道两旁的航标。它能在恶劣环境下长期、连续、全天候工作,每日定时测量并且发报多种水文气象要素。根据外形可分为圆盘形、柱形、船形和球形等,本文针对最常见的圆盘形浮标进行研究。
海洋浮标的系泊系统,是用锚与系泊链把浮标牢固可靠系留在所布放的海区锚位点上,保证其不倾翻、不走锚、不断链和不跑标。对深水海洋浮标,尤其是对其系泊系统展开研究,对我国深水资源的开发和利用具有重要意义[1]。
本文主要根据南海海况为500 m海洋浮标设计一套系泊系统。经过浮标选型、总体设计、水动力分析以及数值模拟系泊方式等研究,验证了当前深水浮标单点系泊的适用性,并得出若干有益结论,对后期类似研究工作有一定的参考价值。
1 深水浮标的水动力分析
1.1 水动力计算模型及水动力特性分析
根据本文设计的浮标尺度,建立其三维模型并进行表面网格划分,见图1。由于研究对象形状较规则,因此可采用混合网格法划分表面网格。最后共划分出节点1 309个,面元1 986个。其中侧面用四边形的面元,底面用三角形面元。
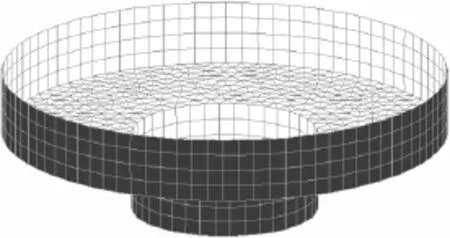
图1 深水浮标几何模型
为降低整个浮标重心、提高浮标的静稳性,浮标在龙骨基线处配置压载重块。根据具体海况,要求浮标在波浪中的垂荡、纵摇和横摇共振周期为2.5~3 s,避开海浪主能量频率,使浮标表现出良好的随浪运动特性。为满足上述要求,设定浮标为圆盘型,主体部分直径2.8 m、厚0.8 m;压载部分直径1.17 m、厚度0.5 m;浮标工作吃水0.9 m,排水量3.056 t。静水中浮标的水线面在主体的中间截面上。
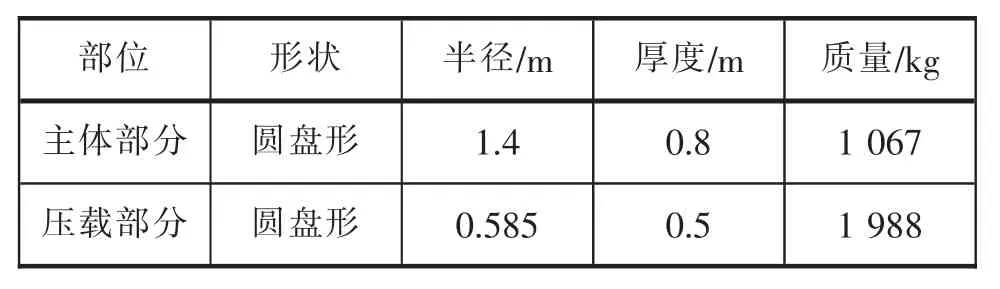
表1 浮标形状及质量分布
重心计算采用组合体重心计算公式:

式中:mi为某个物体的质量;Zi为对应的垂向坐标;M为整个浮标的质量[3]。
根据船舶耐波性理论,浮体自由横摇的近似固有周期为:
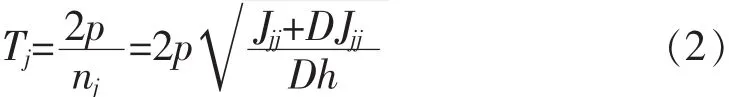
式中:Tj为浮体自由横摇固有周期;nj为浮体自由横摇固有频率;Jjj为惯性矩;DJjj为附加惯性矩;D 为排水量; h 为横稳心高[4]。
将各值代入公式中,可得浮标横摇固有周期约为1.8 s。由对称性可知横摇、纵摇固有周期相同。
同理可由下式算得浮标的垂荡固有周期:
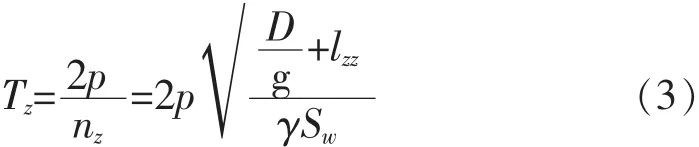
式中:Tz为浮体自由升沉固有周期;nz为浮体自由升沉固有频率;D为浮体的排水量;g为重力加速度;lzz为升沉运动的附加质量;γ为水的重度,且有 γ=ρ·g;Sw为载重水线面积,且 Sw=CwLB,其中 Cw为水线面系数[4]。
由此可得浮标的垂荡固有周期约为2.01 s。至此,浮标的总体设计基本完成,且保证其在海浪中的垂荡、纵摇和横摇共振周期满足要求(2.5~3 s)。其后运动特性计算中输出的响应曲线也证实了这一点。
1.1.1 运动响应模拟计算
在线性假设条件下,浮体的运动幅值与规则波的波幅成正比。模拟浮标在7个不同浪向、不同频率条件下的运动,通过其运动响应输出,考察浮标在垂荡和纵、横摇等主要运动中的幅值变化及其随波运动的特性。
浮标的横摇、纵摇和垂荡是在回复力的作用下做简谐运动而产生,当入射波的频率和浮标的固有频率相同时,浮标运动与波浪运动产生共振,从而在这个频率处横摇和纵摇的运动幅值会达到一个极值,当频率再加大时,与浮标的固有频率岔开,共振也随之消失[5]。
运动响应模拟计算通过水动力计算软件Hydrostar来完成。图2、图3分别给出了浮标的垂荡和纵摇响应曲线。

图2 浮标垂荡响应
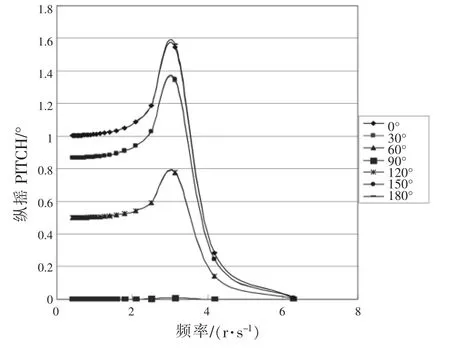
图3 浮标纵摇响应
从垂荡响应曲线中可以看到,共振时的周期约为2.03 s,符合最初浮标设计时的横纵摇周期要求,这也正面验证了浮标的总体设计;另一方面,浮标随海浪一起运动的一段过程中(即垂荡无因次幅值为1时),波浪频率最大值约为2 r/s,对应的波浪周期约为3.14 s,也就是说在波浪周期大于3 s时,浮标能更好随波运动,从而直接反应波浪运动。同理在纵摇响应曲线中也可以看到类似的情况,这说明浮标可以很好的反映波浪周期大于3 s时的波浪运动,与浮标随波运动的设计要求相符。
1.1.2 传递函数的构造
以上模拟计算得到的浮体的运动、速度、加速度和二阶载荷等流体动力相关信息,通过建立转移函数,以函数形式传递至锚泊分析的前期输入中。作为锚泊设计的参数基础,其精确性和重要性是不言而喻的。
2 深水浮标系泊系统设计
2.1 锚泊布置方式
根据相关参考资料,目前浮标主要采用单点单链S型顺应式锚泊系统和单点张紧式锚泊系统。前者主要适用于深水、恶劣的海洋环境条件,整个锚泊系统包括上端顺应式锚泊线,悬浮浮子,底端张紧式锚泊线,海底重力基础锚组成;后者主要适用于海况较为温和的海域,具有系泊浮标水平运动范围小的特点,整个锚泊系统由张力弹簧,张紧式锚泊线,海底重力基础锚组成。
利用锚泊分析软件Ariane7对浮标进行锚泊布置的研究,根据南海海况并考虑到对浮标随波特性的要求,确定此深水浮标的系泊方式为S型单点单链系泊,模拟状态如图4。
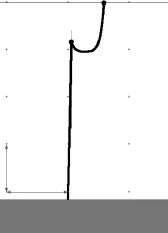
图4 系泊线静态示意图
这根系泊线由两段组成。根据浮标的工作水深及作业海况,选定系泊链的参数如下:在海底与锚连接的一段为第一段,选为钢缆,缆长400 m、直径20 mm;第二段为锚链,与导缆孔相连接,链长400 m、直径20 mm。
2.2 初步设计分析
针对初步设定的系泊线尺寸及材料,数值模拟浮标系泊系统工作状态,对锚链作加载受力分析,先后进行静力计算和时域分析,系泊系统设计及计算采用锚泊分析软件Ariane7完成,表2给出了初步模拟计算结果。
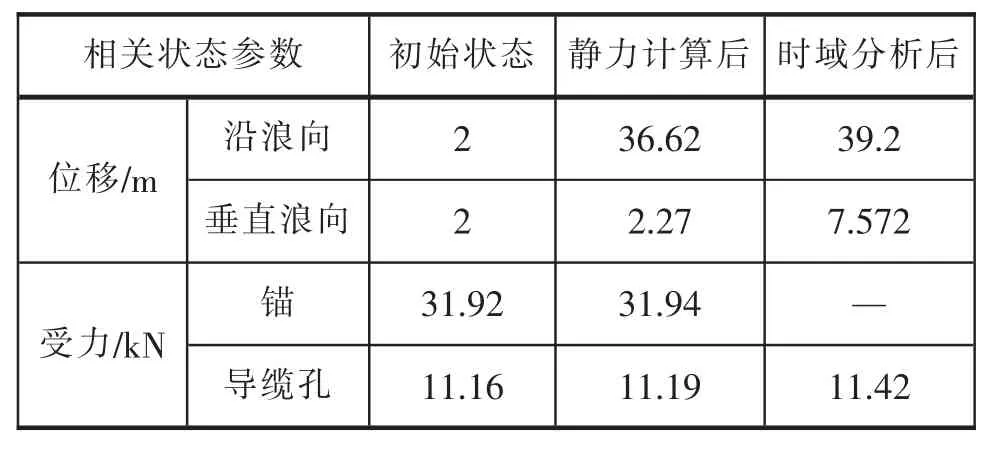
表2 初步设计相关参数
由表2结果知,静力计算后无论是位移还是受力较初始状态均有所增加,其中沿浪向的位移增幅尤其明显,而时域分析后各值较静力平衡后也都有不同程度的增加,除垂直浪向的位移外其余各量增幅不大。
2.3 优化设计分析
对于系泊系统来讲,在强度满足要求的情况下应该存在一组最优方案。因此有必要对初步设计进行优化,即多做几组设计以进行比较分析,从而得到最优方案。优化分析时主要依据时域分析的计算结果。
先从作业工况入手,各组的参数见表3。
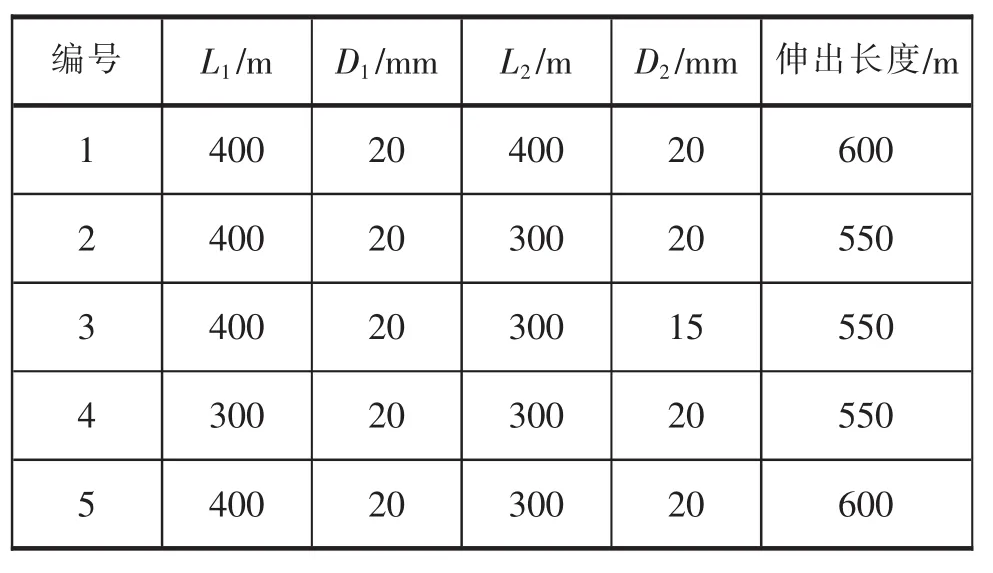
表3 各组系泊链参数对比
表3中:L1表示第一段链长,L2表示第二段链长,D1表示第一段直径,D2表示第二段直径。第二段锚链的破坏载荷:第3组是243.639 kN,其余均为429.088 kN。
经过数据整理,表4给出了时域分析后的沿浪方向的位移及导缆孔处两个方向的张力数据。
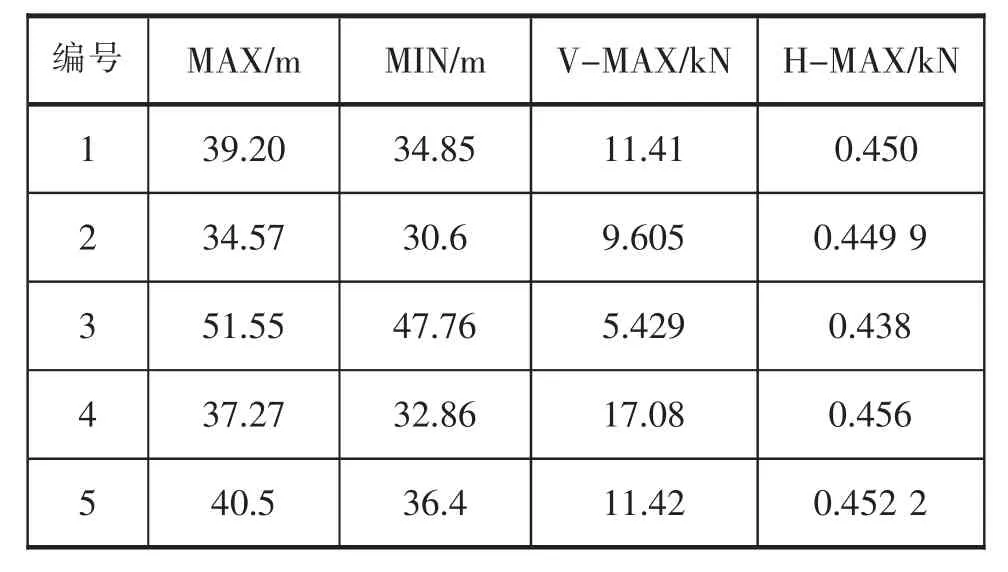
表4 作业工况浮标位移及系泊链受力
表中MAX、MIN分别表示位移最大值和最小值,V-MAX和H-MAX分别表示竖直方向受力最大值和水平方向受力最大值。
结果一目了然。在位移峰值的比较中,第2组的峰值最小,也就是能最好地将浮标限制在固定范围内;再来看锚链在导缆孔处的竖直张力峰值,第3组的受力峰值最小,表现出最好的抗拉能力;水平张力则各组相差不是很多,其中第3组的张力最小。具体分析如下:
(1)位移上看,第2组位移峰值最小,是因为其第二段链长较为适中,且伸出长度也较适宜,这样就有效地限制了浮标工作时的移动范围;其余各组过长或过短都将导致位移的增加。分析如下:第1组与第2组第一段链长相同,但第二段伸出比第2组要长,因此位移会大一些;第3组位移较大是因为其第二段直径的减少,使得第二段锚链的强度韧性降低,不能很好的限制住浮标,也就不能很好的控制浮标的工作范围;第4组与第2组伸出长度相同,但第一段长度不同,于是第二段的长度比第2组要长,因此位移自然会增加。而若是过短,则不太合理。浮标工作水深是500 m,因此作者认为550 m的伸出长度已很短,再短的话,浮标的系泊链就呈现张紧状态,将有悖于开始预定的系泊方式。
(2)受力上看,各组水平张力相近。根据预定的系泊方式,系泊线的第二段呈现一定的悬垂状态,水平上基本受力很小,因此水平张力较为接近。而竖直张力上第3组最小。分析其原因是第3组的第二段锚链直径最小,其锚链的悬垂程度较为缓和,那么锚链在导缆孔处的竖直方向上受力就会小一些;同理,第1组的竖直张力大一些,是其悬垂度过大且直径比第3组要大,因此竖直张力会增加很多;至于第2组比第3组张力大,其原因不排除是直径的增加所致;第4组的张力最大,因为第4组的第一段最短,即其浮筒的位置最深,那么在距水面200 m的竖直距离上仅有250 m的链长,可见其悬垂度过小。简单计算可得到其悬垂度为250/200=1.25,其他各组均要大于此数,也就是说第4组的第二段锚链较为张紧,从而导致锚链受拉过大,而且第4组的水平张力也是最大,这也证实了笔者的分析。
(3)为了再次验证第2组是最优设计,第5组显得尤为重要(相关数据已列于表3及表4中)。在系泊链尺寸与第2组完全相同的情况下,将系泊链的伸出长度改为600 m。从表4的结果分析,其位移峰值大于第2组,受力峰值也比第二组略有增加,这说明尽管系泊链长度适宜,但是过长的伸出长度也会影响浮标的位移,使其工作时的范围增加,不能更好地监测限定范围内的水文要素;同时如前所述,系泊链的伸出长度也不可过短,因为工作水深500 m,所以550 m的伸出长度是较为理想的,这就再次验证了第2组的系泊链尺寸及伸出长度确为最优设计。最终得出了以下结论:在500 m工作水深情况下,浮标的系泊链伸出长度以第2组的550 m为宜,尺寸以第一段400 m加第二段300 m为宜,即第2组的系泊线设计方案最为合理。
(4)综上,给出浮标系泊系统设计的最佳方案,见表 5、表 6。
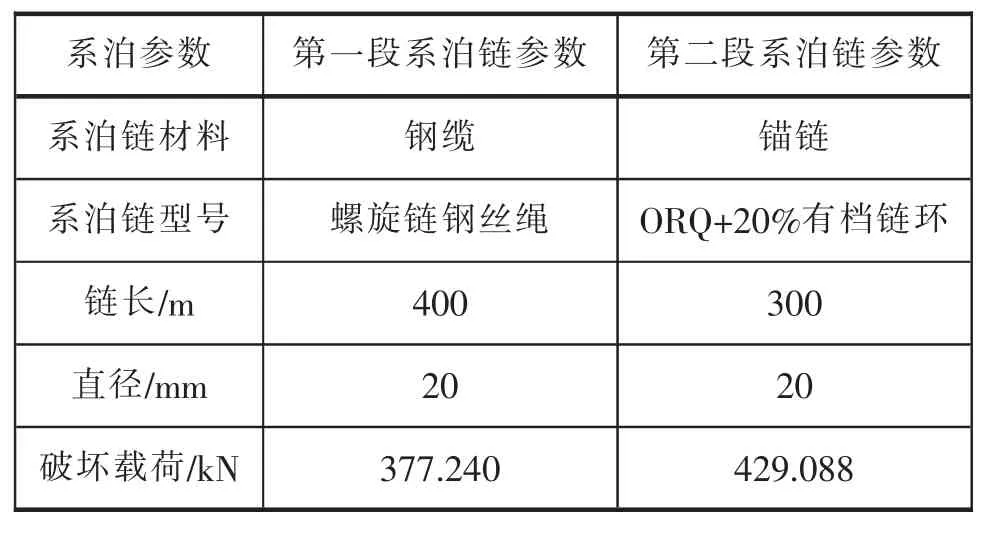
表5 浮标设计最佳方案
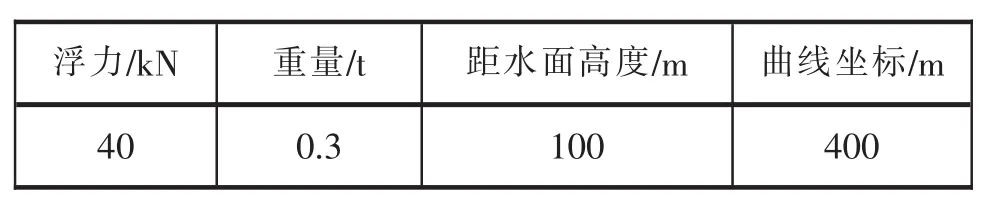
表6 系泊系统浮筒相关参数
2.4 系泊链强度校核
按照API RP 2SK规范相关要求对系泊系统设计分析,需先预测系泊系统的极限响应,如在作业工况和生存工况条件下系泊线的张力;然后将预测值与规范要求值进行校核,以保证系泊线有足够的张力。表7给出了规范的张力极限与安全系数。

表7 API规范中张力极限与安全系数
本设计的强度校核主要针对锚链在导缆孔处的竖直张力进行。表8是准静态及时域分析(动态情况的安全校核系数适用于时域分析)两种海况下,第2组的受力:
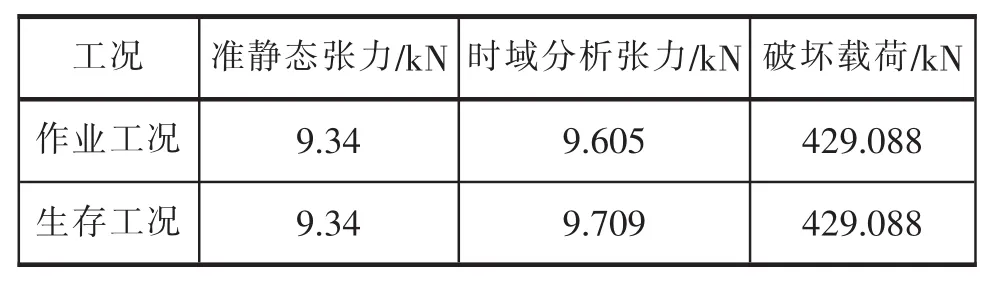
表8 两种分析形态下的受力
首先校核作业工况。准静态下,安全系数约为45.9,远远大于API规定的安全系数2;时域分析下,安全系数为44.67,比API规定的安全系数1.67同样高出很多,可知锚链满足作业工况的强度要求。同样,可知生存工况下锚链强度也满足要求,即在恶劣海况下,此系泊系统的强度稳定性能也十分可靠。
此处给出该系泊系统所选锚的参数:锚的类型取为重力锚,重量约为4 t,材料为钢筋混凝土。
3 结 论
本文由浮标设计开始,经过水动力分析及系泊系统设计,通过具体的数值计算和系泊研究,最终得到最优设计,并由此得出以下结论:
(1)适当的浮标形状给前期研究带来了极大的便利。本次设计选用国际上常用的圆盘形作为浮标的基本形状,使得在研究风、浪、流载荷对系泊系统的影响时,能从任一方向来考察而不影响最终结论。
(2)针对浮标的工作水深,适宜的锚链尺寸将更有效的限制浮标的移动范围,以使其顺利完成固定区域内的气象监测任务,因此本文所做的最优化设计对浮标系泊的相关研究有重要的参考作用
(3)从计算结果上分析,锚和导缆孔的水平张力都非常小,竖直张力也有限值,均在锚链极限强度范围内,由此可见浮标的这种单点单线的系泊方式合理且适用。
综合整个研究过程及本次设计的结论,可以认为:在南海的海洋环境下,此系泊系统既可以满足浮标作业海况下对位移的要求,同时系泊线的强度也满足生存工况的要求。
[1]黄飞龙,吕雪芹,陈刚.海洋气象探测基地——浮标[J].海洋技术,2011(4):62-69.
[2]戴遗山.舰船在波浪中运动的频域与时域势流理论[M].北京:国防工业出版社,1998.
[3]商大中.理论力学[M].哈尔滨:哈尔滨工程大学出版社,2007.8.
[4]李积德.船舶耐波性[M].哈尔滨:哈尔滨工程大学出版社.1991.4.
[5]NEWMAN J N.Ship Fluid Dynamics[M].周树国译.北京:人民交通出版社.
[6]张海彬.船舶运动与波浪载荷三维计算方法研究[D].哈尔滨:哈尔滨工程大学,2001.
[7]BV.Ariane7 Guided Tour[M].[s.l.]:BV,2008.
[8]BV.Ariane7 User guide[M].[s.l.]:BV,2008.
