慢漂运动下多成分锚泊线阻尼参数研究

杨 勇，陈佳欣，黄 山

(1．上海外高桥造船有限公司，上海200137;2．上海外高桥造船海洋工程设计有限公司，上海200137;3．上海振华重工(集团)股份有限公司海上重工设计研究院，上海200125;4．哈尔滨工程大学船舶工程学院，黑龙江哈尔滨150001)

0 引言

海洋浮式平台的定位性能与运动控制是保证油气安全开采与生产的关键因素之一，与动力定位系统相比，传统的锚泊定位系统环境适应性好、可靠性高，在当今世界范围内占据主导地位。某些浮式钻井平台由于作业需要，其水平位移一般不能超过水深的5%［1］，但是浮式平台由于受到二阶波浪力的作用会产生大位移的慢漂运动，因此最大能够占到系统总阻尼80%的锚泊阻尼［2］对于消耗系统能量、限制运动幅度的作用十分关键。Ormberg［3］对浮式平台进行耦合分析，发现锚泊阻尼是系统总阻尼的主要成分，锚泊阻尼对预判平台的运动响应起着重要的作用，应用全耦合分析法将锚泊阻尼效应考虑进整个系统的运动响应分析中是十分必要。Matsumoto［4］通过比较锚泊阻尼和其他阻尼后发现，在低频运动范围内锚泊阻尼是系统总阻尼的主要成分。Johanning［5］总结了锚泊阻尼的所有数值计算方法，分别是基于锚泊线静力分析的准静态法，基于锚泊线动力分析的时域全动态有限元法，以及模型试验法。Kitney［6］应用模型试验法研究了单一成分锚泊线的阻尼特性。Webster［7］对单一成分锚泊线在上部结构物产生波频牵引运动时的锚泊阻尼进行了参数研究。乔东生［8］以单一成分锚泊线为研究对象，应用有限元法比较了上部浮体在发生慢漂运动、波频运动以及两者组合运动时的锚泊阻尼。本文通过对更广泛应用于深水平台的多成分锚泊线进行阻尼参数研究，得到各个参数对锚泊阻尼的影响，以及水动力系数对锚泊线各成分阻尼的影响，所得结论对浮式平台的锚泊系统设计有很大的参考意义。

1 锚泊阻尼定义与计算原理

锚泊阻尼主要由海床与锚泊线摩擦阻尼、锚泊线内阻尼和锚泊线流体动力阻尼3部分组成。海床与锚泊线发生摩擦会产生一部分的系统能量消耗，锚泊线内阻尼由锚泊线内部材料决定，但是这两部分阻尼成分较小，锚泊线流体动力阻尼由作用在锚泊线上的拖曳力引起，这一部分阻尼是锚泊阻尼的主要部分［8］，本文研究重点也是锚泊线流体动力阻尼。

系泊海洋浮式结构物的水平运动方程为:

式中:M为上部结构物质量;Madd为附加水重量;A为运动加速度;Bstr为上部结构物线性阻尼系数;Bmoor为锚泊线性阻尼系数;V为运动速度;K(X)为结构刚度矩阵;X为运动位移;F为运动力。

锚泊线顶端水平张力瞬时值Tx与锚泊线性阻尼系数Bmoor的关系为:

假设锚泊线顶端导缆孔处运动时程与浮式结构物运动时程相同，波浪作用下浮式结构物运动响应为正弦运动，设为X(t)=Aosin(ωt)，其中Ao为运动振幅，运动周期为τ。单根锚泊线在顶端结构物一个正弦振荡周期内所消耗的系统能量E可通过下式进行推导:

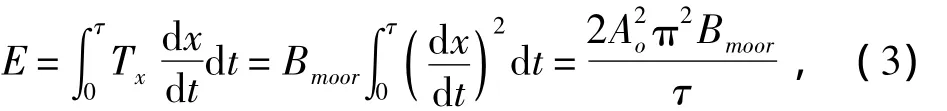
因此，锚泊线性阻尼系数Bmoor可表示为:

锚泊线所消耗的系统能量E需要借助于有限元软件计算所得结果，再结合指示图相关理论来进行求解，具体原理如图1所示。在软件中定义锚泊线顶端水平位移Sx随时间的变化曲线，即输入锚泊线顶端慢漂运动方程，根据有限元动力计算结果，输出锚泊线顶端水平张力瞬时值Tx随时间的变化曲线，并绘制锚泊线顶端水平张力－水平位移曲线，该曲线所围成的面积，即锚泊线在浮式结构物一个纵荡振荡周期内所耗散的系统能量E。

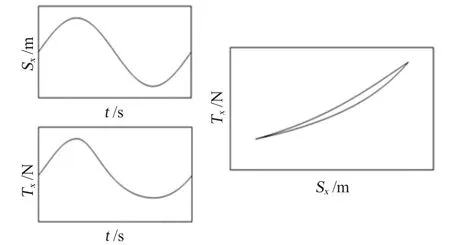
图1 锚泊线顶端水平张力－水平位移指示图Fig.1 Indicator diagram for horizontal tension-horizontal displacement of mooring line top end

2 计算模型与思路

以单根多成分锚泊线为研究对象，顶部段与底部段为钢链，中间段为钢索，设计水深400 m，锚泊线属性如表1所示，锚泊线计算模型如图2所示。

图2 研究模型Fig.2 Model for research

表1 锚泊线属性Tab.1 Properties of the mooring line

利用全动态非线性动力计算软件OrcaFlex进行数值分析，该软件被国外海洋工程界广泛的应用于锚系与立管的水动力分析中。许多文献证实［5，9］，该软件所得结果与试验所得结果十分相近，可靠性很高。锚泊线顶端牵引运动为浮式结构物主要水平运动纵荡运动，通过运行软件进行时域非线性动力计算，绘制指示图得出耗散能量，并计算出锚泊线性阻尼系数Bmoor。

3 计算结果与分析

3.1 海底摩擦系数的影响

考虑到锚泊线流体动力阻尼和海床摩擦阻尼都与锚泊线的顶端运动方程相关，为了进一步理清两者的比例关系，通过表2列举的设计工况研究了存在海底摩擦力和没有海底摩擦力时的锚泊阻尼。从表中结果可以看出，两者之间的结果相差很小，海底摩擦力系数选取0.5时，所有工况的锚泊阻尼增加均不超过10%，这一结论与文献［10］研究成果也相一致，再一次验证了流体动力阻尼是锚泊阻尼的主要成分。在本文后续研究中，海底摩擦系数均设置为0.5。

表2 海底摩擦系数计算参数与结果Tab.2 Calculation parameters and results for variation of seabed friction coefficient

3.2 慢漂运动振幅与周期的影响

表3设计工况研究了锚泊线顶端结构物牵引运动振幅与周期对锚泊阻尼的影响。以300 s为周期不变，顶端运动振幅从30 m到50 m进行变化，以30 m为振幅不变，顶端运动周期从300 s到100 s进行变化。图3(a)和图3(b)分别描述了运动振幅变化对锚泊阻尼影响的指示图和趋势图，图4(a)和图4(b)分别描述了运动周期变化对锚泊阻尼影响的指示图和趋势图。

从图3可发现，随着慢漂运动振幅的增加，锚泊线所消耗的能量增加，锚泊阻尼呈现出近似线性上升趋势。从图4可发现，随着慢漂运动周期的增加，锚泊线所消耗的能量减小，锚泊阻尼呈现出非线性下降趋势。

表3 慢漂运动振幅与周期计算参数与结果Tab.3 Calculation parameters and results for variation of amplitude and period of slow drift motion

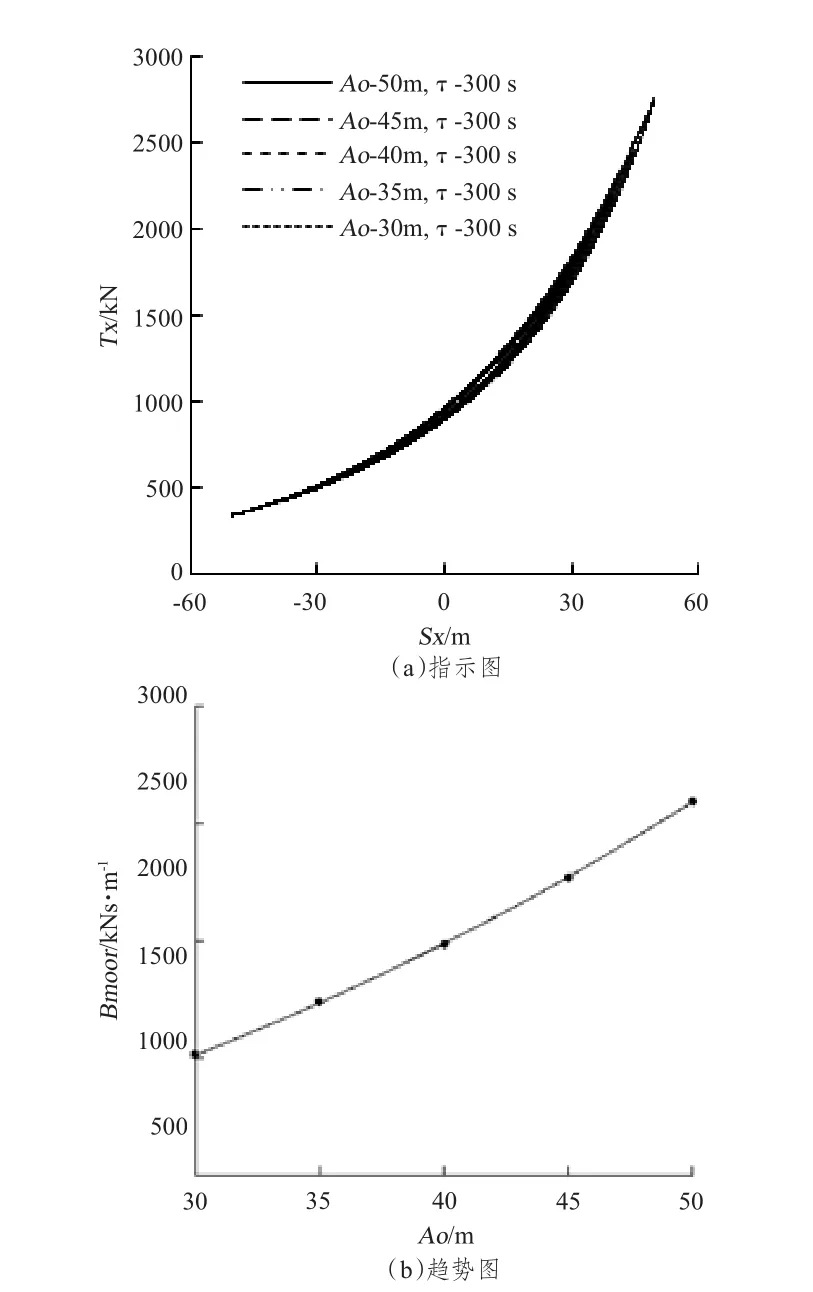
图3 慢漂运动振幅的影响Fig.3 Effect of amplitude of slow drift motion

图4 慢漂运动周期的影响Fig.4 Effect of period of slow drift motion

3.3 流速大小与分布形式的影响

选择2组慢漂运动，海底流速Cspeed分别选取0 m/s，0.5 m/s，1.0 m/s和 1.5 m/s，研究流速变化对锚泊阻尼的影响，设计工况如表4所示。同时，针对其中一组慢漂运动研究流速分布形式Cprofile对锚泊阻尼的影响，流速分布形式沿水深H变化如图5所示，平均流速均为1.0 m/s。

从图6(a)可知，随着流速的增加，锚泊阻尼呈现出非线性上升趋势，无流速情况下2组慢漂运动所产生的锚泊阻尼值相差较大，但随着流速的不断增加，两者之间越来越相近，流速成为决定锚泊阻尼大小的主导因素。从图6(b)可看出，海流均速相同时，不同流速分布形式对锚泊阻尼的影响十分的小，可忽略。

表4 流速大小与分布形式计算参数与结果Tab.4 Calculation parameters and results for variation of current speed and current profile

图5 流速分布形式Fig.5 Current profiles

图6 流速大小与分布形式的影响Fig.6 Effect of current speed and current profile

3.4 垂向拖曳力系数的影响

钢链的垂向拖曳力系数分别选取1.1，1.6，2.4和3.2，钢索的垂向拖曳力系数分别选取1.2，1.6，2.4和3.2，出于研究目的所取数值并不完全在规范［11］推荐取值范围之内。本文研究锚泊线是由3个部分组成，但是顶部段R4钢链长度仅为10 m，验证后对锚泊阻尼影响不大，故不在此给出具体结果。表5设计工况将对剩余两部分垂向拖曳力系数开展参数研究，其中S2代表中间段螺旋钢丝索，S3代表底部段R3S钢链。

从图7可以看出，随着拖曳力系数的增加，锚泊阻尼呈现出近乎线性的增加趋势，并且底部段R3S钢链的拖曳力系数改变对锚泊阻尼的影响较大。导致这一现象产生的原因主要有2点:钢链的拖曳直径要大于钢索的拖曳直径，因此利用莫里森方程计算拖曳力时，钢链拖曳系数的改变导致作用在其上的拖曳力改变更大;钢索的运动响应位移与钢链相比也较小，如图8所示，划线上部为钢索 (除顶端有10 m钢链)，下部为钢链。

表5 垂向拖曳力系数计算参数与结果Tab.5 Calculation parameters and results for variation of normal drag coefficient

图7 垂向拖曳力系数的影响Fig.7 Effect of normal drag coefficient

图8 锚泊线法向位移比较Fig.8 Comparison of transverse displacement of the line element

3.5 垂向附加质量系数的影响

表6设计工况研究了锚泊线垂向附加质量系数改变对锚泊阻尼的影响，从表中所列结果可看出，无论是改变中间段螺旋钢丝索还是底部段R3S钢链的垂向附加质量系数，锚泊阻尼值几乎不变，该系数对锚泊阻尼影响不大。

表6 垂向附加质量系数计算参数与结果Tab.6 Calculation parameters and results for variation of normal added mass coefficient

4 结语

通过对一根应用于实际工程的多成分悬链式锚泊线进行时域非线性动力分析，计算能量耗散与锚泊阻尼值，可得出以下结论:

1)海底摩擦力所引起的海床摩擦阻尼与拖曳力引起的流体动力阻尼相比很小，存在海底摩擦力时，锚泊阻尼大约增加5%至7%;

2)随着慢漂运动振幅的增加亦或是周期的减小，锚泊线消耗能量上升，锚泊阻尼值变大;

3)随着流速的增加，锚泊阻尼值呈现非线性上升趋势，并且成为主导锚泊阻尼值大小的决定性因素，在海流均速相同的情况下，不同流速分布形式对锚泊阻尼值的影响很小;

4)锚泊线垂向拖曳力系数的改变对锚泊阻尼值的影响很大，随着该系数的增加，锚泊阻尼值呈现出近似线性上升趋势，并且底部段R3S钢链的垂向拖曳力系数改变对锚泊阻尼值影响更大;

5)锚泊线垂向附加质量系数的改变对锚泊阻尼值的影响很小。

［1］ 黄祥鹿，陆鑫森．海洋工程流体力学及结构动力响应［M］．上海:上海交通大学出版社，1992:102．

［2］ HUSE E，MATSUMOTO K．Mooring line damping due to first-and second-order vessel motion［C］//Offshore Technology Conference．Houston，1989:135 －148．

［3］ ORMBERG H，LARSEN K．Coupled analysis of floater motion and mooring dynamics for a turret－moored ship［J］．Applied Ocean Research，1998，20:55 －67．

［4］ MATSUMOTO K．The influence of mooring line damping on the prediction of low-frequency vessel motions at sea［C］//Offshore Technology Conference．Houston，1991:119－128．

［5］ JOHANNING L，SMITH G H，WOLFRAM J．Measurements of static and dynamic mooing line damping and their importance for floating WEC devices［J］．Ocean Engineering，2007，34:1918 －1934．

［6］ KITNEY N，BROWN D T．Experimental investigation of mooring line loading using large and small-scale models［J］．Journal of Offshore Mechanics and Arctic Engineering，2001，123:1 －9．

［7］ WEBSTER W C．Mooring-induced damping［J］．Ocean Engineering，1995，22(6):571 －591．

［8］ 乔东升，欧进萍．深水悬链锚泊线粘性阻尼计算［J］．海洋工程，2009，27(4):16 －22．QIAO Dong-sheng，OU Jin-ping．Calculation on viscous damping of deepwater catenary mooring line［J］．The Ocean Engineering，2009，27(4):16 －22．

［9］ BROWN D T，MAVRAKOSS．Comparative study on mooing line dynamic loading［J］．Marine Structures，1999(12):131－151．

［10］乔东升，欧进萍．深水悬链锚泊线阻尼计算［J］．振动与冲击，2011，30(2):24 －31．QIAO Dong-sheng，OU Jin-ping．Damping calculation of a deepwater catenary mooring line［J］．Journal of Vibration and Shock，2011，30(2):24 －31．

［11］ DNV．Environmental conditions and environmental loads(DNV －RP－C205)［S］．Norway，2010:52－62．