基于偏最小二乘回归分析法的汽车4S店客户满意度研究

姚层林

（武汉商业服务学院 湖北 武汉 430056）

一、引言

顾客满意度作为顾客满意的量化统计指标，描述了顾客对产品的认知（期望值）和感知（实际感受值）之间的差异，可以测量顾客满意的程度。当顾客的认知小于感知时，顾客的满意度就高；反之，当认知大于感知时，满意度就低。

美国的顾客满意度指数（ACSI，American Customer Satisfaction Index）模型（如图1所示），已成为影响最为广泛的模型。

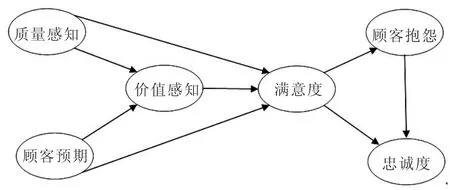
图1 美国满意度指数（ACSI）模型

本文借鉴了国内外对于顾客满意度的研究成果和实践经验，结合我国4S店销售中的实际特点以及实际的可操作性，运用偏最小二乘法（PLS）对4S店销售中的客户满意度模型进行处理。

二、汽车4S店客户满意度数据处理及分析

本文选用2010年第四季度东风悦达起亚汽车用户满意度调研数据，用单因变量的偏最小二乘回归计算其顾客满意度二级指标数值。其中三级指标17个，如表1所示。通过软件PEW 中单因变量的偏最小二乘回归计算顾客满意度，如图2所示。

1、自变量之间的相关关系

自变量之间的相关系数r的绝对值在0.5到0.8之间，说明两个变量是显著性相关，自变量之间的相关系数r的绝对值在0.8到1之间，说明两个变量是高度线性相关。经过计算，我们可以看到大部分变量间相关系数值在0.8到1之间，说明是高度线性相关。变量之间存在高度线性相关，采用偏最小二乘回归将显示出其优越性。

2、提取的主成分对变量的解释能力

在偏最小二乘回归计算过程中，所提取的自变量成分t1，一方面尽可能多地代表X中的变异信息，另一方面又尽可能与Y相关联，解释Y中的信息。主成分t1对自变量X和因变量Y的解释能力分别为：86.10%，99.74%。如表2。

3、自变量与因变量的相关关系

判断自变量集合X与因变量集合Y之间是否存在较强的相关关系是检验是否可以建立Y对X的线性回归的基本条件，如果在图3中明显观察到t1与u1之间存在线性关系，则说明X与Y有显著的相关关系，这时采用偏最小二乘回归方法建立Y对X的线性模型才会是比较合理的。自变量与因变量相关系数R2为0.9974，自变量与因变量存在高度线性相关关系。t1与u1相关关系见表3、图3。

4、自变量在解释因变量时的作用

变量投影重要性指标VIPj值，用来测度每一个自变量在系统分析中的作用，即xj在解释Y时作用的重要性。

根据用变量投影重要性指标VIPj来测度的每一个自变量对解释因变量的作用大小依次为：x52＞x43＞x23＞x13＞x11＞x41＞x32＞x22＞x51＞x21＞x53＞x42＞x33＞x34＞x31＞x12（如表 4、图4）。根据VIPj＞1即认为xj在解释因变量时具有重要作用的原则，x52、x43、x23、x13、x11、x41、x32、x22、x51 在解释 y 具有重要作用。其中x52在解释y具有最重要的作用，x43、x23、x13在解释y也具有重要作用。

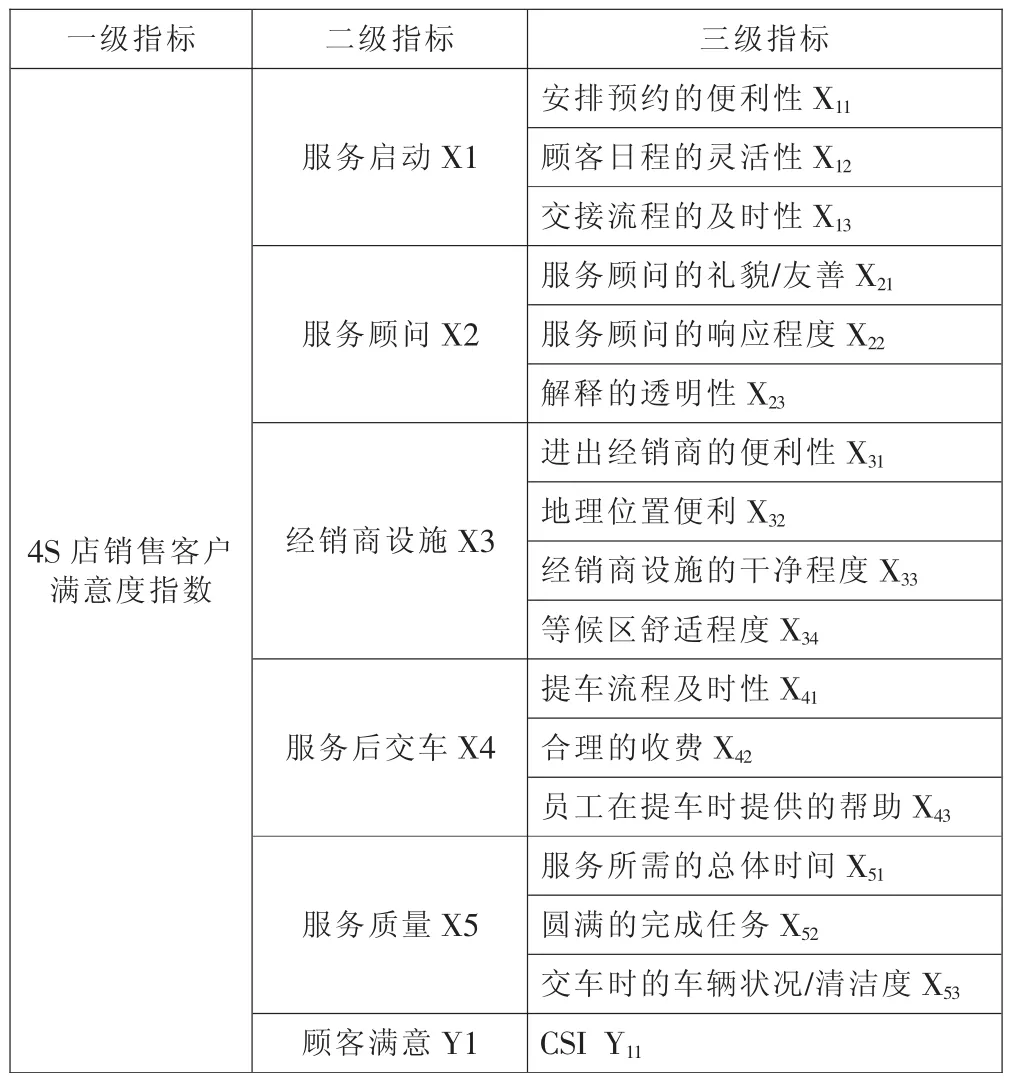
表1 4S店销售客户满意度指数量表

图2 PLS操作

表2 主成分对变量的解释能力

5、组间相关关系的结构分析

在r（，t1）/r（，t2）关系图上（如图5），如果xj与y两变量的位置十分接近，则认为它们的相关关系相当密切。另一方面，团聚在一起的自变量xj之间，也存在着较强的相关关系，相隔很远的自变量xj之间，由于相关系数较低，可认为是互不影响的独立变量。

6、特异点的发现及处理

如果有数据出现在椭圆图之外，一般就是特异值，我们要进行剔除。从图6中我们发现，所有数据都在椭圆图之内，所以样本数据存在着0个特异点。

7、偏最小二乘回归原始数据数学模型

偏最小二乘法的回归模型为：y=-0.5868+0.0487x11+0.0755x12+0.0771x13+0.0729x21+0.0863x22+0.0536x23+0.0703x31+0.0673x32+0.0789x33+0.0466x34+0.0758x41+0.0478x42+0.0694x43+0.0658x51+0.0601x52+0.0626x53

通过模型我们发现除了截距为负值之外，其他变量的系数都为正数，说明自变量对因变量都是正相关的。提高任何一项服务都能提高顾客的满意度。

其中0.0863（服务顾问的响应程度）＞0.0789（经销商设施的干净程度）＞0.0771（交接流程的及时性）＞0.0755（顾客日程的灵活性）＞0.0729（服务顾问的礼貌/友善）＞0.0703（进出经销商的便利性）。所以我们要提高客户的满意度，这要从这几个指标重点入手。

表3 t1与u1相关关系

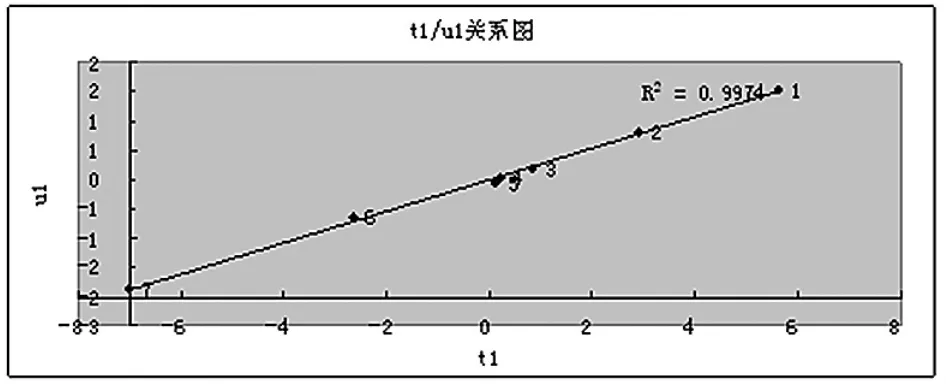
图3 t1与u1关系图

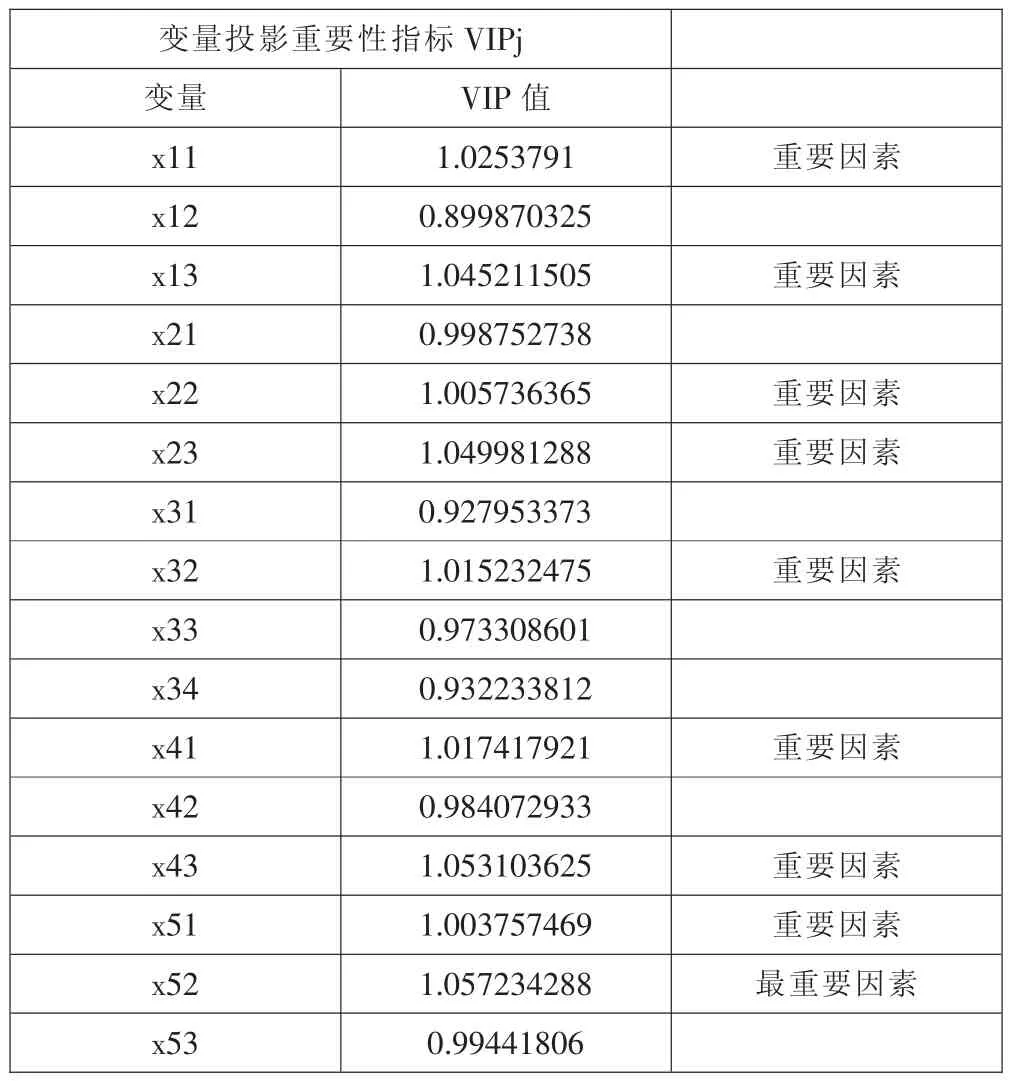
表4 变量投影指标

图4 VIP值柱状图

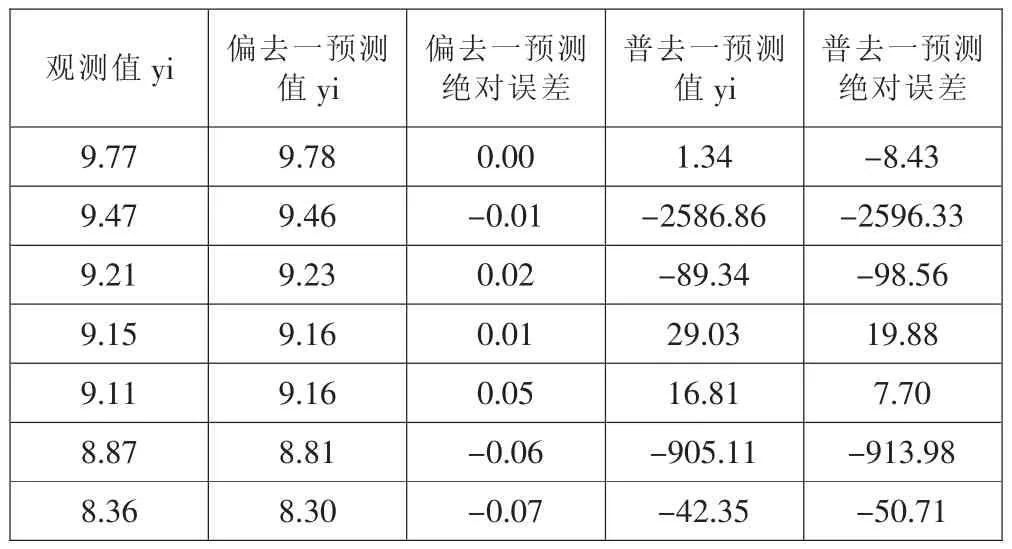
表5 偏最小二乘与普通最小二乘去一回归预测比较

8、偏最小二乘与普通最小二乘去一回归预测比较

回归预测比较是指将原始样本数据逐一删除样本点i，其余数据经偏最小二乘与普通最小二乘回归后再用二模型计算的yi的预测值，并与原始数据的y值进行比较（如表5）。

偏最小二乘法预测绝对误差（|偏最小二乘预测值yi-观测值yi|）平均值=0.0314＜普通最小二乘法预测绝对误差（|普通最小二乘法预测值yi-观测值yi|）平均值=527.9403

偏最小二乘法预测相对误差（（|偏最小二乘法预测值yi-观测值yi|）/观测值yi%）平均值=0.0036＜普通最小二乘法预测相对误差（（|普通最小二乘法预测值yi-观测值yi|）/观测值yi%）平均值=56.8284

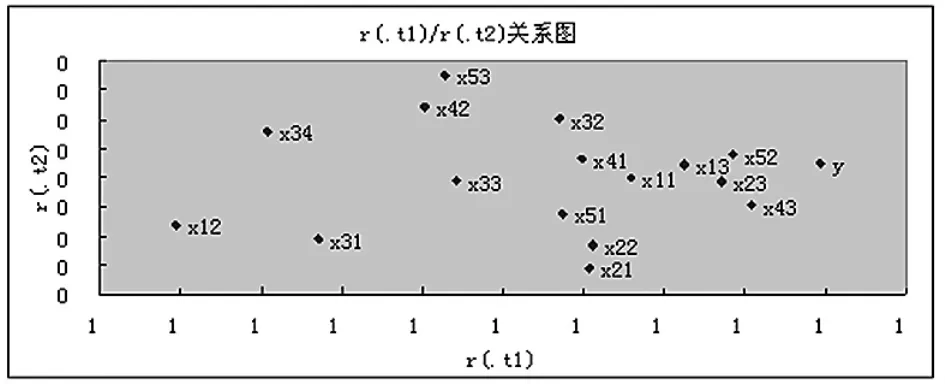
图5 r（，t1）/r（，t2）关系图

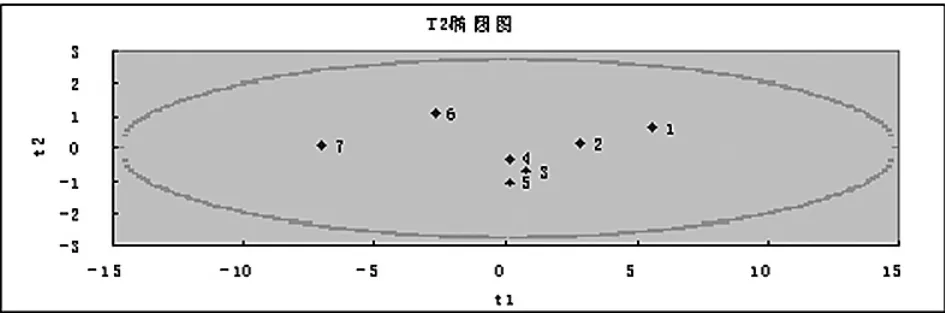
图6 特异点发现表

图7 偏最小二乘与普通最小二乘去一回归预测比较柱状图

偏最小二乘法预测残差平方和=0.0114＜普通最小二乘法预测残差平方和=7589114.1819

回归预测结果表明，偏最小二乘回归在对新出现数据的预测方面表现出比普通最小二乘回归更精确的性能，也说明偏最小二乘回归分析更接近事物的真实，更加稳健。

三、提高4S店销售客户满意度建议和措施

根据0.0863（服务顾问的响应程度）＞0.0789（经销商设施的干净程度）＞0.0771（交接流程的及时性）＞0.0755（顾客日程的灵活性）＞0.0729（服务顾问的礼貌/友善）＞0.0703（进出经销商的便利性），我们要提高客户的满意度，首先要提高服务顾问中的服务顾问的响应程度，然后要提高经销商设施中的经销商设施的干净程度、服务启动中的交接流程的及时性、顾客日程的灵活性、服务顾问中的服务顾问的礼貌/友善、经销商设施中进出经销商的便利性这几个指标。

[1]王俊喜、马骊歌：关于汽车企业提高客户满意度的对策分析[J]. 汽车工业研究，2010（10）.

[2]陈高波：基于核偏最小二乘回归的顾客满意度指数模型[J].科教文汇（下旬刊），2010（11）.

[3]郭辉、刘贺平：基于核的偏最小二乘特征提取的最小二乘支持向量机回归方法[J].信息与控制，2005（4）.

[4]Roman R.Kernel Partial Least Squares for Nonlinear Regression and Discrim ination.Neural Network World，2003，13（3）.