一个新的超混沌系统及其电路实现*

申朝文，禹思敏

(①广东工业大学 自动化学院，广东 广州 510006；②仲恺农业工程学院 信息学院，广东 广州 510225)

0 引言

近年来，随着混沌系统理论的不断完善，越来越多的研究表明，超混沌系统与一般混沌系统相比具有更为复杂的拓扑结构和动力学行为，它能在混沌保密通信和混沌信息加密上提供更为可靠的保证，具有较好的工程应用前景。因此，越来越多的研究者在现有混沌系统上进行改造，提出了一系列的超混沌系统[1-5]，以及如何构建超混沌系统的方法。可见对超混沌的研究已经成为了混沌应用领域中一个重要的研究热点。

1 新的四维超混沌系统

文献[6]给出了一个新的三维二次多项式自治系统，其无量纲方程为：

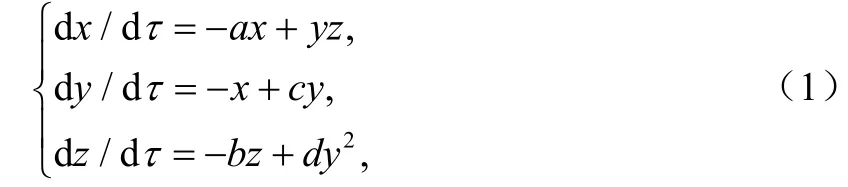
当a=20，b=5，c=10，d=7时，系统(1)处于混沌状态。3个Lyapunov指数分别为：，系统的3个平衡点为：平衡点O的特征值为：= 10,= 10,= -5，平衡点 E1和 E2处的特征值为=-1 8.2601，=-1.63±10.3379i。因此，系统(1)具有一个鞍点和两个稳定的鞍焦平衡点。

要产生超混沌系统必须满足两个必要条件：①对于自治系统而言，至少是四维；②至少有两个正的Lyapunov指数且所有Lyapunov指数之和小于零。根据以上两个条件，在系统(1)的基础上引入一个反馈控制器u，令u的变化速率为d/dueyτ=-，并把控制器u反馈到系统(1)的第二个方程中，构造出一个可产生超混沌现象的四维自治系统，其状态方程为

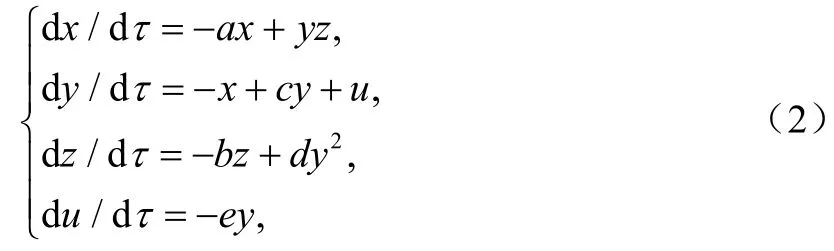
当 a = 20，b =5，c = 10，d =7，e = 13.5，系统(2)的4个 Lyapunov指数分别为=2.2259，=0.2069，=0，=-34.9259，有两个正的Lyapunov指数，系统处于超混沌状态，对应的几个典型的超混沌吸引子相图如图1所示。

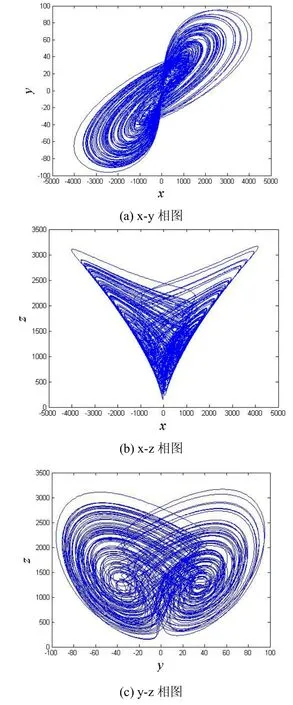
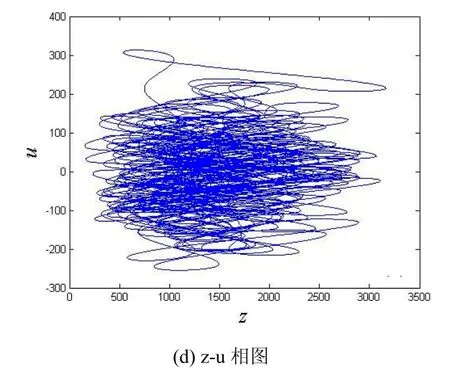
图1 超混沌吸引子相图

2 新超混沌系统的动力学分析

2.1 系统的耗散性

2.2 平衡点分析

令 系 统(2)的 每 一 个 方 程dx/dτ =dy/dτ =得系统平衡状态方程为：

由式(3)计算得，系统(2)有唯一平衡点)0000(，，，O，它与系统参数的取值无关，在平衡点O处线性化系统(2)，得到对应的Jacobian矩阵为：

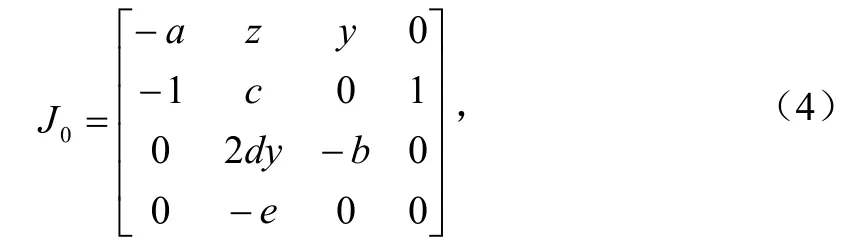
取系统(2)参数 a = 5 0,b = 7 .5,c = 2 5,d = 7 .5,e =13.5时，计算出平衡点O处的特征值为= 0.5522，= 24.4478，=-50，= -7.5，因此O是一个不稳定的鞍点。

2.3 Lyapunov指数谱图与分岔图分析

随着系统参数的改变，系统平衡点的稳定性将会发生变化，从而系统也将处于不同的状态。固定参数 a =50， b=7.5，c=25，d =7.5，使参数e在(0，90]之间变化，系统初始值取(1，2，500，4)，随参数e变化的Lyapunov指数谱和变量x的分岔图分别如图2和图3所示。需要说明，图2中并未给出始终处于最大负值的Lyapunov指数。

从图2可以看出，当e∈(0，0.3)时，系统的Lyapunov指数都小于或等于零，系统处在周期态或拟周期态。e ∈ [0 .3，0.7)时，系统存在一个正的Lyapunov指数，系统处于混沌状态；而e∈[0.7，50.4]时，系统有两个正的 Lyapunov指数，系统处于超混沌状态。当e∈(5 0.4，74.3]时，系统至少有一个正的Lyapunov指数，系统在混沌态和超混沌态来回转换，形成复杂的动力学行为。当 e ∈(7 4.3，79.7]时，系统有一个正的Lyapunov指数或者最大的Lyapunov指数为零，系统处在混沌态或复杂周期态。当e∈(79.7，90]时，系统处在拟周期态或周期态。随着e的继续增加，最大Lyapunov指数趋近于零，意味着系统的解最终演化为一个周期轨。

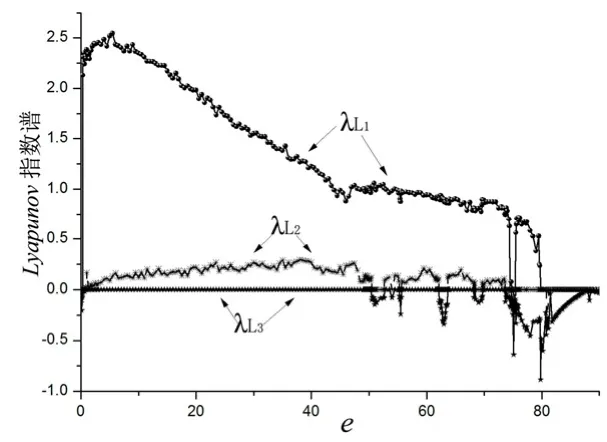
图2 Lyapunov指数谱

图3 系统分岔

3 超混沌系统的电路设计与实现

根据式(2)设计实现该四维超混沌系统功能的实际电路[7-8]，采用线性电阻，线性电容，运算放大器为AD712，由于系统存在非线性项，可选用乘法器AD633实现。必须注意的是，变量 x , y ,z,u各自的动态范围大约[-4000,4000],[-1 00,100],[100,3200],[-2 50,320]。远大于运算放大器的饱和电压，故必须进行变量比例压缩变换，才便于电路实现。对系统(2)进行非均匀变量比例压缩变换，令x, y ,z,u 压缩到原来的 1 / 1000，1/20，1/1000，1/100，由于系统变量的变换不影响系统的状态及性能，从而系统(2)可变为：将参数 a =50， b=7.5，c=25，d =7.5,e =13.5代入式(5)，并作时间尺度变换，令 τ =，= 100，得：

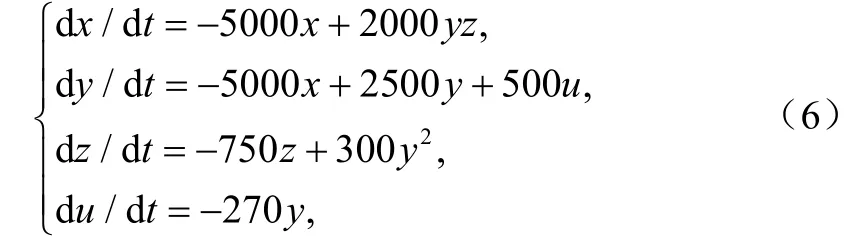
对式(6)进行模块化电路设计，如图4所示。

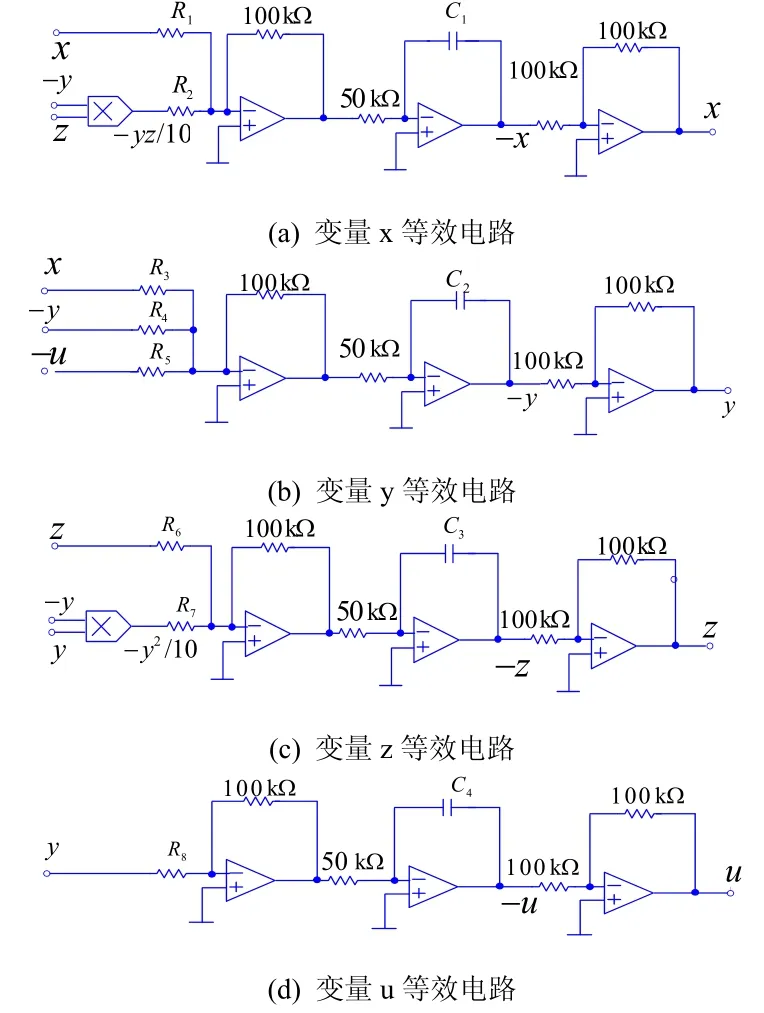
图4 超混沌电路设计

电路的状态方程为：

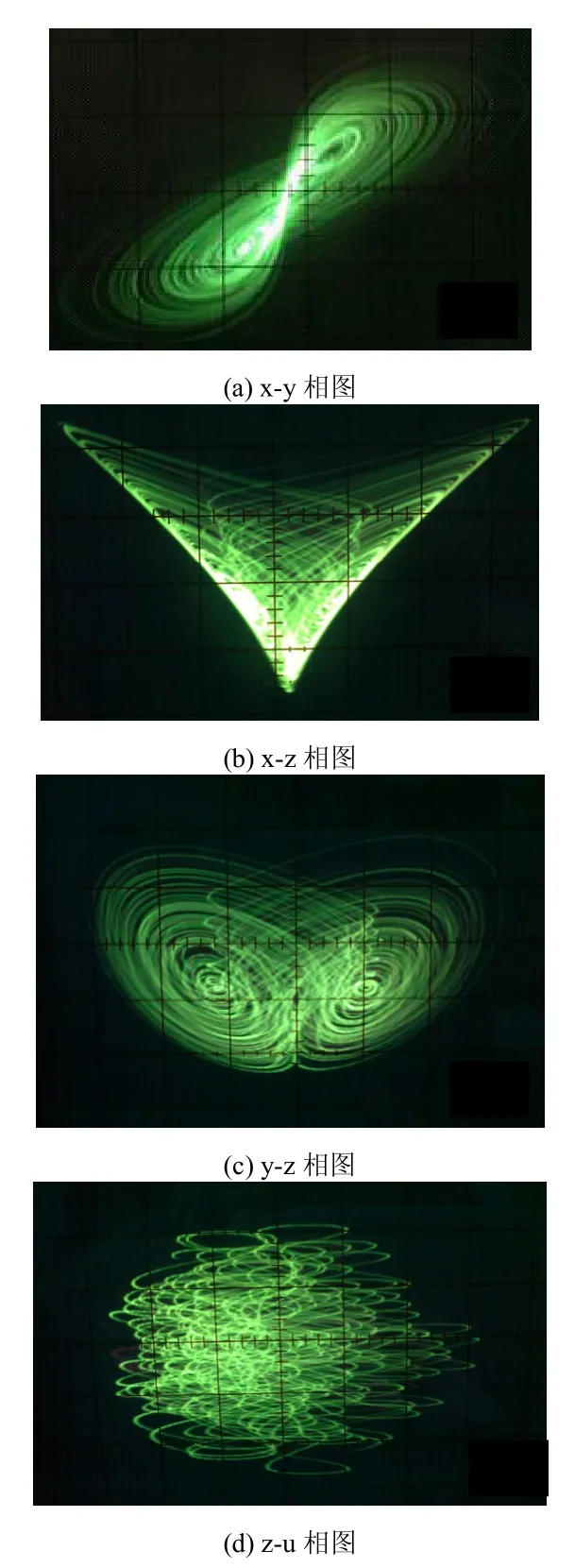
图5 电路实现超混沌吸引子相图

4 结语

通过对一个三维二次自治系统中引入一个变量反馈控制器，构造出一个新的超混沌系统，对系统的动力学特性进行了相关的理论分析与数值仿真，可以得出该系统与其他超混沌系统相比[9-10]，具有较大的正李雅普诺夫指数，且在较广的动态参数范围内存在超混沌轨道。最后设计并实现了该超混沌系统的硬件电路，给出了相关电路的实验结果，证实该超混沌系统具有较为复杂的拓扑结构，在混沌保密通信等领域具有潜在的应用前景。

[1] CHEN Z,YANG Y,QI G, et al. The Generation and Circuit Implementation of a New Hyper-chaos based upon Lorenz System[J].Physics.Letter.A,2007(361):78-86.

[2] 王光义,郑艳,刘敬彪. 一个超混沌 Lorenz吸引子及其电路实现[J]. 物理学报,2007,56(06):3313-3320.

[3] 满峰泉,侯承玺.一个新的超混沌系统设计与实现[J].通信技术,2010,43(11):108-111.

[4] 刘扬正.超混沌 Lü 系统的电路实现[J].物理学报,2008,57(11):1439-1443.

[5] BAO B. Hyperchaos from an Augmented Lü System[J].Int.J. Bifurcation and Chaos,2010,20(11):3689-3698.

[6] 禹思敏.混沌系统与混沌电路—原理、设计及其在通信中的应用[M].西安:西安电子科技大学出版社,2011.

[7] 包伯成,刘中,许建平.一类超混沌系统电路实现及其动力学分析[J].四川大学学报,2010,42(02):182-187.

[8] 谢国波,禹思敏,周武杰.一个新的三维二次自治混沌系统及其研究[J].通信技术,2009,42(01):267-270.

[9] 黄爱美,李欣,马宝艳. 基于二维超混沌序列的交替加密[J].信息安全与通信保密,2007(01):125-126,130.

[10] 张辉,陈建国.嵌套混沌变参映射的构造及分析[J].信息安全与通信保密, 2008(07):51-52,55.