一种改进的DSSS信号扩频码估计算法研究

张 焱，熊 刚

（中国电子科技集团第三十研究所，四川 成都 610041）

0 引言

直接序列扩频信号由于具有强抗干扰性、低截获概率、能够抑制多径效应等特点，已经广泛应用于信息保密、卫星、航天、全球定位系统（GPS）、测距和码分多址（CDMA）通信等方面。直接序列扩频信号的功率谱密度通常很低，频谱上表现为信号被噪声所淹没，具有抗干扰性[1]，而且提供了较高的保密性，它还具有克服频道资源紧张问题等优点[2]。由于扩频码的一些特性，在截获DSSS信号之后，若已知 DSSS信号的有关参数——扩频码周期和码速率等，则对DSSS信号扩频码的估计将成为可能，这对该类扩频通信系统的抗截获性能分析具有重要意义。离散卡洛（K-L）变换定理等表明特征值分解的过程可以实现从DSSS信号中估计出扩频码序列，但它的计算量、存储量都相当大[3]。文中利用改进的协方差矩阵迭代的思路进行扩频码估计，大大降低了运算量，而且收敛的性能也优于参考文献中提出的投影子空间跟踪算法[4]和基于神经网络的扩频码估计算法[5]。

1 信号模型

经过AWGN信道后，接收到的基带DSSS信号模型为：

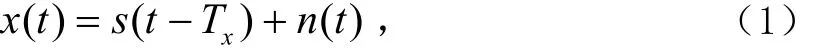
2 传统的协方差矩阵迭代算法

传统的协方差矩阵迭代算法的思路：用收敛的权值逼近主特征向量，则可以避免直接进行特征值分解的庞大运算量和存储量，相比特征值分解算法具有更好的可实现性。当采用主特征向量估计码序列时，扩频码序列估计就转变成了提取主特征向量的问题。设{x(t)}t≥0是n维的数据向量，其估计的协方差矩阵可以根据如下方程递归得到：

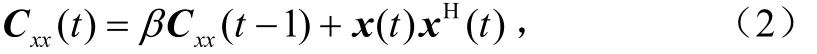
为了跟踪子空间权值矩阵W(t)，协方差矩阵迭代方法在每次迭代时包含数据压缩和正交归一化两步：

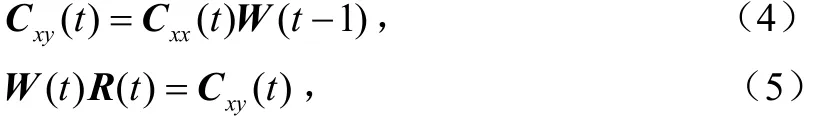
3 改进的算法及仿真分析

3.1 改进的基于协方差矩阵迭代的算法

将式（2）代入式（4）中得到：

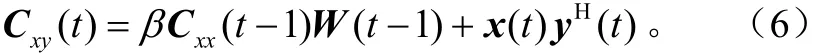
应用新的投影逼近方法：

式中，Θ(t)=WH(t-1)W(t)不必接近单位矩阵。在t-1时刻应用式（6），式（5）可以用式（7）递推：

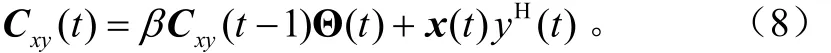
改进的协方差矩阵迭代算法主要思想是基于矩阵()tΘ的一种特殊选择，可以减少总体的运算复杂度。令：

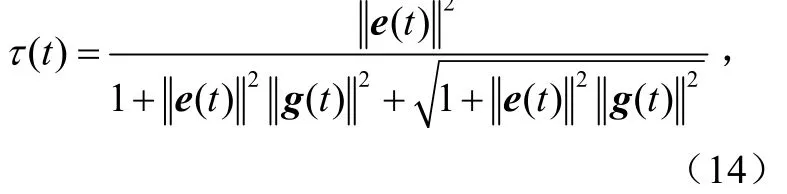
直接的计算表明了rr×维Hermite矩阵：

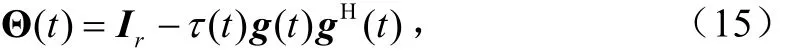
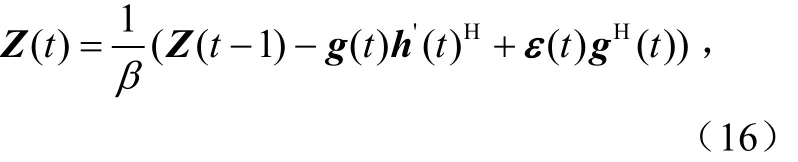
最后，得到：

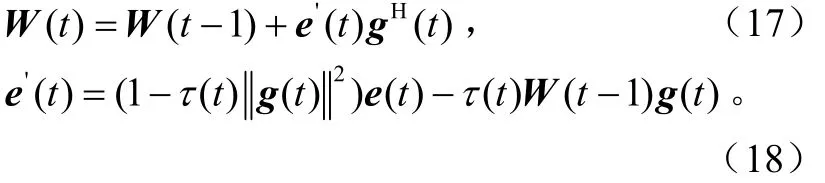
3.2 仿真实验及性能分析

引入扩频码估计结果序列的相关性这个衡量指标，它是指当估计出的扩频码序列与实际序列逐比特比较时，一致的数目减去不一致的数目。用以下公式来表示：

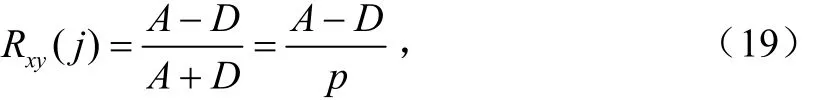
式中，A是估计出的扩频码序列 x和实际扩频码序列y的对应码元相同的数目，D是对应码元不同的数目，p是扩频序列总码元数。相关性xyR 的数值越大，估计出的扩频码序列的准确度越好。以下实验均是进行500次Monte Carlo仿真的平均结果。

仿真实验 1 对不同码长的扩频序列进行估计，码周期分别取为P=127，P=511和P=1 023，DSSS信号采用 Gold序列。考察改进的协方差矩阵迭代算法在不同信噪比下，估计出的扩频码序列与原始扩频码序列之间的相关性能。信号观测采样数据组数N=200。

由图1可知，当SNR大于-14 dB时，改进的协方差矩阵迭代算法估计不同码长序列的结果与对应的原始扩频码序列的相关性都大于0.9，完全达到了性能要求。

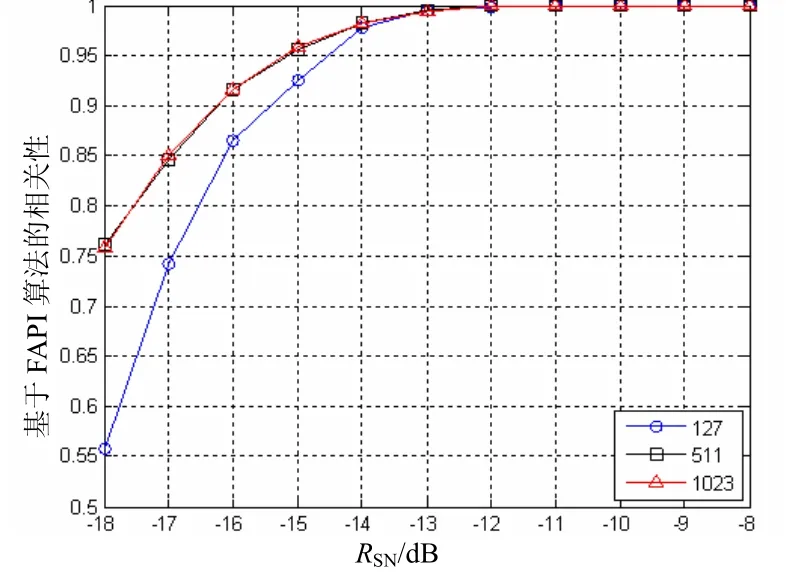
图1 不同码长的扩频码估计结果的相关性比较

仿真实验2 扩频码序列周期取P＝1 023，采用Gold序列。分别采用基于投影子空间的算法，基于神经网络的算法和改进型的协方差矩阵迭代算法进行扩频码序列估计，其中，基于投影子空间的方法的性能曲线用三角形标注，基于神经网络的方法的用方形标注，改进型的协方差矩阵迭代方法的用圆形标注。比较3种方法估计得到的扩频码序列和原扩频码的相关性。如图2所示，改进的协方差矩阵迭代算法正确估计PN码序列得到结果的相关性更优。

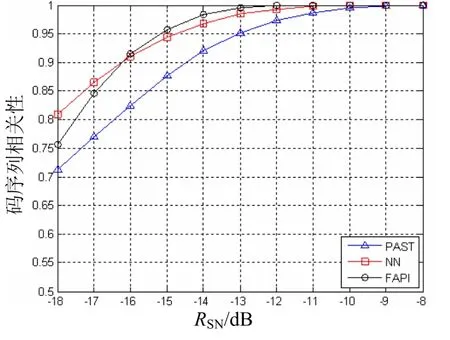
图2 不同算法的扩频码估计结果相关性比较

仿真实验3 图3是信号扩频码周期为1 023，采用Gold码序列时，基于神经网络的算法、基于投影子空间的算法和改进的协方差矩阵迭代算法收敛所需采集数据组数均值曲线。3种方法中，相同信噪比下改进的协方差矩阵迭代方法的收敛数据组数均值要小些，即算法收敛所需采集的信号数据组数更少，意味着估计信号扩频码序列所需的侦测时间更短。

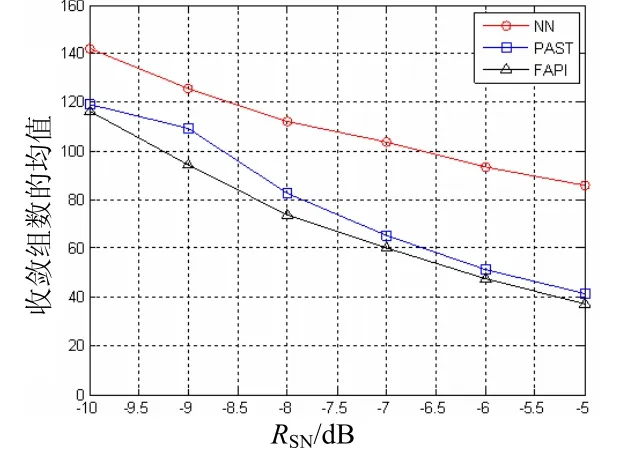
图3 收敛数据组数均值曲线

4 结语

为解决通信监测等应用领域中低信噪比下的直接序列扩频信号的扩频码序列估计问题[6-7]，文中研究了一种改进的协方差矩阵迭代算法。算法设计时综合考虑了估计性能和运算量，适用于对直接序列扩频信号的多种扩频码序列估计，理论推导和计算机仿真都验证了算法的效果。协方差矩阵迭代算法得到的结果序列的相关性要比基于投影子空间的方法好，信噪比容限更低。同时该方法还具有运算量小，易于硬件实现等特点。随着直接序列扩频通信技术的发展，对DSSS信号扩频码的估计算法将起到更加重要的作用。

[1] 一种基于软件无线电技术的扩频通信系统[J]. 通信技术,2009,42(06):52-55.

[2] 直接扩频技术的仿真以及实现[J]. 通信技术,2007,40(09):1-2.

[3] BUREL G, BOUDER C. Blind Estimation of the Pseudo-random Sequence of a Direct Sequence Spread Spectrum Signal[J].IEEE-MILCOM, 2000, 2(10):967-970.

[4] 欧阳聪星,周建,乐光新.一种直接跟踪信号子空间特征成分的新算法[J].北京邮电大学学报,2008,23(02):38-42.

[5] 张天骐,林孝康,周正中.基于神经网络的低信噪比直扩信号扩频码的盲估计方法[J].电路与系统学报,2007,12(02):118-123.

[6] 金光浪, 宋茂忠.数字混沌序列在DSSS通信中的误码率仿真[J].信息安全与通信保密,2007(06):60-61.

[7] 刘波.一种实现高保密强度卫星通信的途径[J]. 信息安全与通信保密,2007(08):112-114.