基于图形电磁学的雷达散射截面计算方法改进
2012-08-09刘立国张国军莫锦军袁乃昌
刘立国 张国军 莫锦军 袁乃昌
(1.国防科技大学电子科学与工程学院微波中心,湖南 长沙410073;2.空军雷达学院黄陂校区雷达维修教研室,湖北 武汉430435)
引 言
图形电磁学(GRECO)[1-2]作为一种重要的电磁仿真方法,由于其在仿真电大目标上的优势而受到青睐。图形电磁学结合了传统高频方法[3]和计算机图形学,采用计算机图形学的目标渲染功能从而省去了在传统高频方法中耗时的可见面判断与网格剖分过程。利用物理光学法来计算每个可见面对电磁散射的贡献,采用物理绕射方法计算棱边对电磁散射的贡献。
GRECO的优势在于利用显卡的深度缓存算法来实现不可见面的消隐,达到了加速仿真计算进程的目的。利用渲染过程的栅格化过程代替面元剖分过程、渲染生成的像素代替传统高频方法中的面元,既节省了内存又极大地加快了仿真速度。
但是在传统GRECO方法中,仅仅能够获得渲染后像素的位置和像素所对应面元的法矢信息,无法应用于计算双站雷达散射截面、多次电磁散射等方面。并且其计算精度严重依赖于屏幕分辨率,使得可仿真的最大目标电尺寸受限。
针对传统GRECO的不足,提出了基于像素信息还原目标几何信息的方法,实现快捷的双站RCS计算,同时结合弹跳射线法(SBR)计入多次反射的影响;针对其计算精度受屏幕分辨率的限制,研究了离屏计算的可能性,进一步提出了基于帧缓存对象(FBO)的图形电磁学方法,扩展了GRECO的应用范围和仿真电大尺寸目标的能力。
1 传统图形电磁学
利用物理光学法计算目标的电磁散射特性时,需对目标做面元剖分和消隐处理,得到对散射有贡献的面元进行计算。图形电磁学方法结合了物理高频方法和计算机图形学,实现了仿真计算的加速。
目标在计算机中的渲染过程就是OpengGL(图形硬件的一种软件接口)的工作过程,它是一种过程性而不是描述性的图形API.如图1是OpengGL的完整工作流程。

图1 计算机的渲染流程
了解OpenGL的工作流程对于理解图形电磁学的工作机理和研究扩展应用有着重要作用,离屏计算等思想均是受此启发。
传统图形电磁学的工作流程如下:首先,计算机通过程序读取目标的几何信息包括顶点、面元、法向矢量及其纹理等;其次,在设定了特定渲染条件下,进行光栅化过程;最后,进行片元操作(包括深度缓存比较等)。在图形电磁学方法中利用光栅化过程代替传统物理光学法中剖分过程,利用深度缓存算法来实现不可见面的消隐过程,由于上述两个过程都是在硬件上执行的,达到了利用硬件加速的目的。利用物理光学法即可得到图形电磁学下雷达散射截面的计算公式

其中:λ为照射平面波波长;θ为入射平面波与像素所对应面元法向矢量的夹角;z为观测点到面片的距离(此处一般为深度缓存有关的数值),积分是在可见面元上进行的。
2 RCS计算方法改进
2.1 双站雷达散射截面的计算
传统图形电磁学只能计算单站雷达散射截面,然而双站雷达散射截面往往是我们感兴趣的参数,比如在反隐身研究中对单站雷达具有隐身效果的目标在双站雷达条件下往往不具备隐身效果。许多学者利用单双站等效原理来研究双站散射问题,把双站散射计算等效为单站散射的计算[4-5],通过公式(2)进行计算

式中:β为双站夹角;σb和σm分别为双站和单站雷达散射截面。然而,这种方法是一种近似方法,只在双站夹角不大且目标形状比较光滑时才成立。
杨正龙等人[6]进行了基于像素信息进行双站雷达散射截面通用计算的研究。基于文献[6]的思想,重点研究重构目标几何信息的过程,得到更为简单和通用的计算方法。
在传统GRECO计算雷达散射截面(RCS)的过程中,仅仅获取了面片的位置及其法向矢量,这些信息对于计算双站RCS是不足够的。在忽略沿观察方向任何表面流的影响条件下,根据Stratton-Chu方程,远区散射场为[7]

其中:i和s为入射方向和观察方向的单位矢量;S表示目标被平面波照射部分;n为面片dS的法向矢量。考虑相位信息,可得到包含相位信息的雷达散射截面计算公式

其中,er为观测方位的电矢量方向。
由于采用的渲染像素为四边形(一般是正方形),所以采用Gordon求和形式的计算公式[8]来进行计算:

此公式主要的参数是am、r0、rm,以图2为例来进行说明。图2(a)中,面元S在全局坐标系中位置为r0,在图2(b)中的局部坐标系中按照逆时针方向可以通过多边形的顶点坐标bn获取边长的矢量信息am和边长的位置信息rm.得到了投影后的像素信息及其投影面片的方向矢量。为了使用公式(5)进行双站RCS的计算,需要得到每个像素对应的投影之前的多边形信息(这里是平行四边形),即am、r0、rm.通过读取像素信息,利用投影的逆过程可以得到这些信息以用于计算。对这点进行说明:以y-z平面为例,图3是y-z平面内的投影过程,S是投影前多边形的一条边,P是投影后像素的一条边,Δy是像素y方向棱边对应的实际长度。为了还原S边的几何信息,通过读取投影后对应像素的位置(x,y,z)和S边的法向矢量 (nx,ny,nz)(即S所在多边形的法向矢量)来得到计算所需的全部信息。通过简单的三角形相似关系可以得到
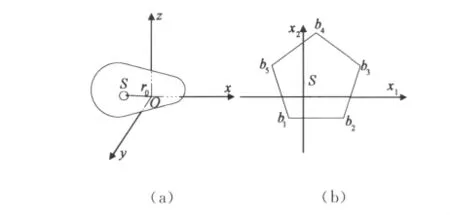
图2 面元S的坐标示意图

图3 y-z平面内边的投影

得到了棱边S的全部信息。同样的方法可以应用在x-z平面内即可得到多边形的全部棱边信息,利用公式(5)即可得到目标的双站RCS.
为了验证计算方法的正确性给出直径为2m的金属球在水平和垂直两种极化、频率为4GHz的平面波照射时双站RCS特性。
图4中实线是水平极化入射时RCS的双站散射特性,空心圆曲线是垂直极化入射时的双站RCS散射特性。在双站角为0时(即后向散射),金属球的RCS为5.08dB,几乎与理论值5dB一样。同时从图5中看出结果并未完全关于180°对称,这是由于输入的模型为面元模型,与理论模型相比存在一定的误差,实际模型的不完全对称导致了结果误差。
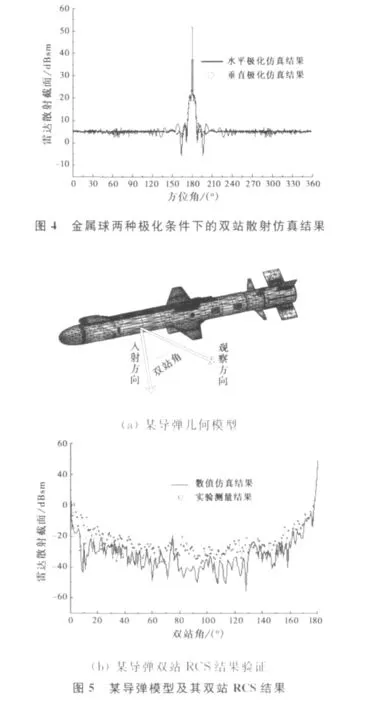
利用本节方法计算某导弹(模型如图5(a))在水平极化、频率为10GHz的平面波正侧视入射条件下的双站RCS结果,如图5(b),导弹的尺寸为4.845m×0.813m×0.813m.其中空心圆加点曲线为实际测量结果,实线是本文的仿真结果。从图中可以看出本节的计算方法和实测结果基本一致,进一步验证了算法的准确性。仿真结果略低于测量结果是由于未考虑多次反射的影响。
2.2 多次反射计算
将讨论射线追踪与图形电磁学的结合来计算具有腔体结构目标的多次散射电磁特性。传统的图形电磁学只能够计算一次反射的结果,而一般的射线追踪方法存在着计算耗时、计算资源需求大的缺点。如果能够将两者的优缺点进行互补性的结合将带来计算的极大加快、计算资源需求的极大降低。
射线追踪方法[9-10]是一种高频近似方法,对入射平面波作几何光学近似,即认为平面波是在射线管内按照直线传播,射线管外并无能量和场强的泄漏。当射线管遇到目标时产生反射和折射,并记录路径上的场强变化,最后在选定的口面上进行积分。由于其过程符合物理规律,计算结果较为准确,但是在处理电大目标时,存在着计算速度慢、计算资源占用多等缺点,难以在个人电脑上得到应用。图形电磁学在网格剖分和消隐面处理上的优势决定了它能够很好地互补射线追踪方法。通过两者的结合使得在降低计算需求,加快计算速度的同时能够获得目标多次反射的电磁散射特性。
以像素对应的面元为单位进行射线追踪,进行多次反射计算,流程如图6所示。在金属目标或者表面涂敷情况下,仅需考虑反射射线追踪,记录每次反射射线的场强作为下一个像素的入射射线。记录每条反射射线处的像素并应用上一节的双站RCS计算方法可获得此像素对电磁散射的贡献。

图6 像素的射线追踪流程
以边长17.9cm的90°二面角为例来验证多次反射的正确性。在频率为9.4GHz、水平极化状态平面波照射下,结果如图7所示。在0°~270°之间的区域没有多次反射贡献的区域,计算结果和平板散射的结果一致,而在270°~360°的区域有明显的二次反射带来的影响,并且仿真结果和理论计算结果一致。

图7 边长17.9cm二面角的二次散射结果
2.3 离屏计算
传统图形电磁学的计算精度依赖于屏幕分辨率,例如屏幕的分辨率为2 500×1 600时,能计算的目标二维投影最大电尺寸为250λ×160λ.因此其计算范围受到了极大的限制,为了克服这个缺点,学者们提出了分屏计算的方法[11-13]即目标分区显示、计算,最后将计算结果相叠加。这种方法在一定程度上扩展了图形电磁学的仿真范围,但是这种方法不适合2.2节中研究的多次反射计算。本节中提出了基于帧缓存对象的离屏计算方法,这种方法不但可以用于多次反射的计算,而且可以提高算法本身的精度。
如图1所示,在目标渲染到屏幕之前计算机会把渲染所需的全部信息存储在帧缓存中,按照屏幕的分辨率将这些信息渲染到屏幕上。在仿真计算的过程我们只需得到这些信息用于计算,不需要将其渲染到屏幕之上。省去这一过程可以克服计算精度依赖屏幕分辨率的缺点。
在 OpenGL3.0中引入了帧缓存对象[14],可以根据计算需求和硬件限制来创建所需的帧缓存区。通过将目标渲染到创建的帧缓存对象中,从中提取计算所需的信息即可用于图形电磁学的计算。目前帧缓存对象能够创建的最大分辨率为(6×104)×(6×104),可计算的电尺寸为6 000λ×6 000λ,仿真的目标电尺寸有了很大增加。
以直径2m的金属球为例来验证离屏计算的准确性。在频率4GHz、水平极化平面波照射下及离屏渲染的像素3 000×3 000,金属球的后向RCS结果如图8所示。
从图8中的曲线可以看到计算的结果接近理论结果,与使用屏幕渲染结果对比容易得到结论:使用离屏渲染计算可以得到更为精细、准确的结果,从而验证了此方法的正确性。在传统的图形电磁学中,需要从屏幕读取计算所需信息。屏幕渲染过程RGBA信息共同分享32位通道,每一个颜色信息只能占用8位通道数。而利用帧缓存对象离屏渲染技术每一个颜色分量都可以占用32位通道。因此获得的浮点精度可以达到更高,计算精度相应可以达到更高,在处理低散射目标时浮点本身的精度尤为重要。

图8 金属球的离屏计算散射结果
3 结 论
研究了传统图形电磁学的缺点和不足,针对这些缺点和不足提出了基于像素信息还原模型几何信息的双站RCS计算方法以及多次反射的计算。同时把基于帧缓存对象的离屏渲染方法应用到图形电磁学中,可以克服计算精度受屏幕分辨率限制的缺点。最后通过一些实例的验证和比较,可以看出这些扩展应用的正确性及其应用前景。
在进行双站散射计算时,利用了渲染后像素的逆投影过程,得到物体表面剖分后的面元,这其中有一定的近似,在面元法矢与入射波方向夹角不大时,像素所代表的实际尺寸小于λ/10时即可认为还原后的面元可代表物体的实际表面。当两者之间的差距较大时,可引进余弦函数进行处理。但是处理低散射体时,要严格研究这种近似关系的影响,目前国内外尚无这方面的报道,这也是本文的后续工作之一。
利用帧缓存对象的离屏图形电磁学方法需要从显卡中回读信息,这一过程较为耗时。在多次反射计算过程中,需要软件实现z-buffer算法来保存面元深度信息,这一过程也比较费时。如果把这些处理过程也放在显卡中运行可省去回读过程,能够加快计算速度,如何把上述过程运行在显卡或图形处理器(GPU)上是我们下一步工作的方向。目前单显卡可计算的最大电尺寸为6 000λ×6 000λ,如何处理更大的电尺寸目标,采取多显卡或多GPU并行处理是可行的方法。英伟达公司发布了基于GPU编程的CUDA语言,可实现上述功能。实现基于CUDA的多显卡和多GPU并行算法是我们未来的工作重点。
[1]RIUS J M,JOFRE L.High-frequency RCS of radar targets in real time[J].IEEE Antennas and Propagation Magazine,1993,41(9):1308-1319.
[2]RIUS J M,FERRANDO M,JOFRE L.GRECO:graphical electromagnetic computing for RCS prediction in real time[J].IEEE Antennas and Propagation Magazine,1993,35(2):7-17.
[3]周文明,宋建社,郑永安,等.复杂目标电磁散射混合算法[J].电波科学学报,2007,22(5):884-890.ZHOU Wenming,SONG Jianshe,ZHENG Yongan,et al.A hybrid method for computing high-frequency RCS of complex radar targets[J].Chinese Journal of Radio Science,2007,22(5):884-890.(in Chinese)
[4]RUCK G T,BARRICK D E,STUART W D,et a1.Radar Cross Section Handbook[M].New York-London:Plenum Press,1970.
[5]BUDDENDICK H,EIBERT T F.Acceleration of raybased radar cross section predictions using monstaticbistatic equivalence[J].IEEE Trans Antennas Propagation,2010,58(2):531-539.
[6]YANG Zhenglong,JIN Lin,NI Jingling,et al.Bistatic RCS calculation of complex target by GRECO[J].Acta Electronica Sinica,2004,(6):1033-1035.
[7]KNOTT F E,SHAEFFER F J,TULEY M T.Radar Cross Section[M].Raleigh:Scitich Publishing Inc,2004.
[8]GORDON W B.Far-field approximation to the kirehhoff-helmholtz representations of scattered field[J].IEEE Trans on Antennas and Propagat,1975,23(5):590-592.
[9]LING H,CHOU R C,LEE S W.Shooting and bouncing rays:Calculating the RCS of an arbitrarily shaped cavity[J].IEEE Trans Antennas Propagat,1989,37(2):194-205.
[10]WEINMANN F.Ray tracing with PO/PTD for RCS modeling of large complex objects[J].IEEE Trans Antennas Propagat,2006,54(6):1797-1806.
[11]严靖峰,徐鹏根.RCS预估中图形电磁学方法的改进[J].电波科学学报,1998,13(3):313-317.YAN Jingfeng,XU Penggen.Improved methods for graphical electromagnetic compuing in RCS prediction[J].Chinese Journal of Radio Science,1998,13(3):313-317.(in Chinese)
[12]张云飞,马 骏.复杂目标GRECO方法的分屏显示[J].北京航天航空大学学报,2005,32(12):1332-1336.ZHANG Yunfei,MA Jun.Multi-screen display calculation method of GRECO for complex targets[J].Journal of Beijing University of Aeronautics and Astronautic,2005,32(12):1332-1336.(in Chinese)
[13]汪蔚霞,王宝发.图形电磁计算法在双站散射计算中的工程扩展[J].电波科学学报,2004,19(3):258-262.WANG Weixia,WANG Baofa.Application of the GRECO method to bistatic scattering simulation[J].Chinese Journal of Radio Science,2004,19(3):258-262.(in Chinese)
[14]SHREINED D.OpenGL编程指南[M].季 军,译.北京:机械工业出版社,2011:332-341.
