改进的统一Hu 矩在图像目标识别中的应用

张 琪，屈 严，董志芳

(东南大学电子科学与工程学院，南京 210096)

当今社会，图像识别与检索已经成为我们正常生活中如影随形的一项技术。但是由于在图像获取及传输过程中的数据丢失，图像一定程度上会发生畸变，故而直接基于灰度图的图像识别早已不能满足当今时代的要求。Hu 于1962年提出了用于区域形状识别的连续函数不变矩［1］，不变矩特征由于其在图像平移、伸缩、旋转时均保持不变，而且具有全局特性，已成为图像识别的主要方法之一。但是，在离散状态下Hu 矩的比例不变性并不成立［4］，针对这一问题，许多学者进行了相应的研究工作。首先，由Chen 实现了离散状态下的比例不变性［2］，但是对边界情况没有考虑;之后，杜亚娟、王波涛、徐学强等人又相继在前人的基础上提出了改善的不变矩算法［3－7］，最终将区域、边界和离散状态都考虑在内。但是，徐学强等人的算法在图像识别的效率上具有一定的局限性，因而，我们在文献5 的基础上进行了优化。经过大量的识别实验，结果表明，本文的不变矩算法具有良好的不变性，同时提高了图像在尺度变换中识别率，同时针对图像旋转变换的特点［8］，通过引入权向量一定程度上消除了识别的误差，进一步提高了旋转变换后的识别率，是一种更加稳定的不变矩算法。

1 Hu 矩的定义［3－4］

一幅M×N 图像f(x，y)的(p+q)阶原点矩和(p+q)阶中心矩分别定义为:

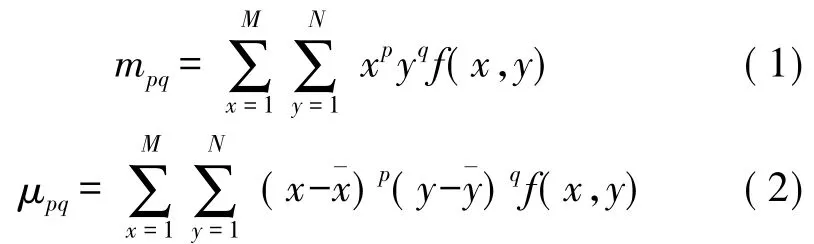
其中，(¯x，¯y)为图像f(x，y)灰度质心。

归一化的中心距定义为:

Hu 利用归一化的二阶和三阶中心距构造了7个不变矩函数值式，这7个函数式对于平移、旋转、尺度变换都具有不变性。为了方便计算我们只取前4个不变矩，分别用φ1、φ2、φ3、φ4表示。

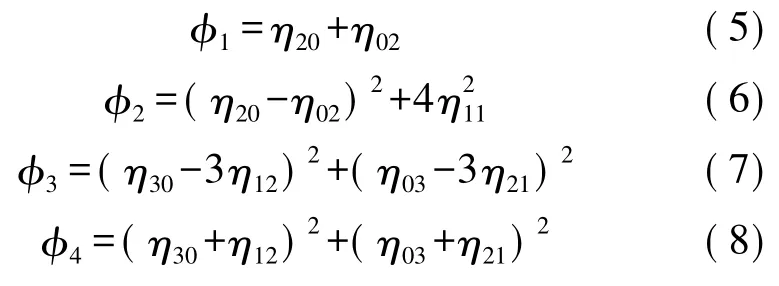
2 改进的统一Hu 矩

2.1 改进的统一Hu 矩

文献［5］证明了在离散状态下，Hu 定义的7个不变矩的比例不变性是不成立的。因此需要对Hu进行改进，但该方法在应用中具有一定的局限性，因此我们改进了文献［5］的统一Hu 矩，构造出新的，但同样适用基于区域矩、边界矩、离散状态的归一化中心矩，具体如下所示:

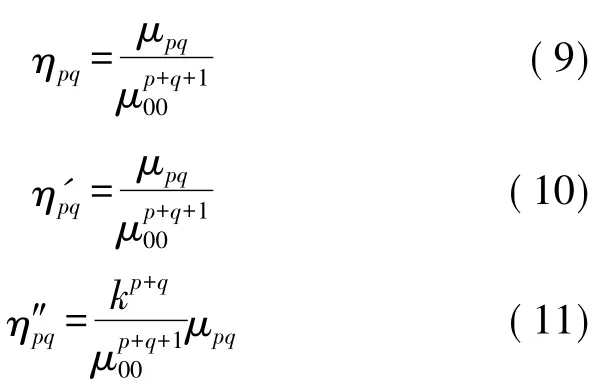
其中k值表征的是尺度变换后新坐标点相对于原坐标点的伸缩的倍率。

根据k值表征的意义，要得到离散状态下不变矩，就必须消去此伸缩倍率。基于这种思想，我们在文献［5］中的统一Hu 矩的基础上，进一步改进的不变矩如下:

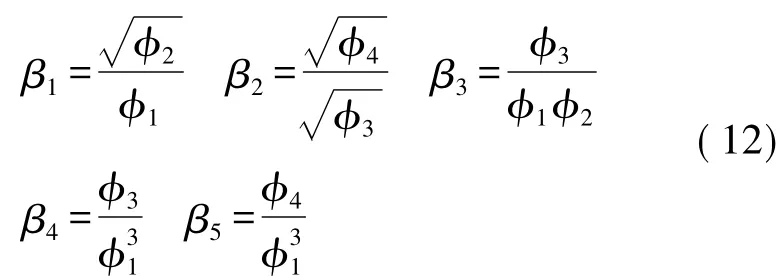
可以证明:对于区域、边界、离散的情况，不变矩的公式是统一的，但由于篇幅所限这里不作证明。

2.2 统一Hu 矩的在旋转状态下改进

上文已经说明，在区域、边界、离散情况下，不变矩的公式是统一的，于是我们在图像的识别上就不考虑边界效应的影响，因此对于图像的识别就集中在对统一Hu 中5个参数的利用和判别上。

在原点矩和中心距的定义式(1)、式(2)中，图像经过角度θ(初始角度设为θ0，(¯x，¯y)为灰度质心，Δx，Δy 表示待旋转点相对于质心的坐标)的旋转后，新图像变为f(x′，y′)，于是我们可以得到:

根据μpq的定义可得:

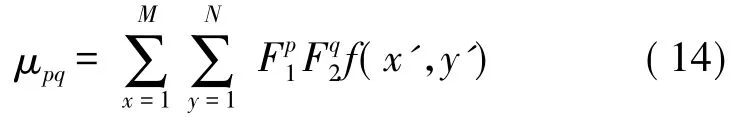
其中F1=p1×cos(α);F2=p2×sin(α)，并合并为F=p×cos(α+φ)。

故μpq将包含有Fp+q+1，Fp+q两项，而μ00则只包含有F 的1 次方项。对于前一项，在归一化中心距的计算中由于和μ00的阶数相同，因而在归一化中心距的计算中会消去，因此不予考虑。对于第二项，在归一化中心距的计算中会留下F－1项，导致后边的计算产生误差。为了消除误差，引入权向量A，根据各矩所需的需消误差来分配权值。

对A* 归一化即可得到权向量A。

在行业交流方面，联盟共举办三届“全国BIM联盟联席会”，邀请各省市BIM联盟参加，通过每年举办一届联席会，加强全国各BIM联盟之间交流；走访联盟观察员单位，与装配式钢结构民用建筑产业技术创新战略联盟进行工作交流；受香港科技大学（The Hong Kong University of Science and Technology, HKUST）和香港建造业议会（The Construction Industry Council,CIC）的邀请参加“全球BIM标准现状”技术论坛。

每个统一矩对于相似度的贡献自然不同，根据实际应用的同一类图像在得到图像旋转各个角度的矩后，除以原图像的各个矩的值进行归一化处理，然后每个矩用最大值减去平均值可以近似的得到a值。于是我们得到了5个a值a1，a2，a3，a4，a5，也得到了向量A*，归一化后得A。

定义图像识别的目标函数为:

S 用以表征图像间的相似度，越小表示相似度越高，识别性越好。

3 实验及结果分析

为了验证改进的统一Hu 矩对图像识别的有效性，我们选用图1所示的4 类图像进行类间图像识别实验，通过比较其目标函数的大小来进行图像识别。每副图又分别经过平移、旋转和尺度变换各产生26副实验样本图像，继而进行类内相似度匹配实验。

图1 四幅不同类型的图像

3.1 类间特征数据分析

图1为4 类样本的基准图，表1 给出了相应的矩不变量，及另外3 幅图与目标图像的相似度比较。

对于目标图像可以选取图像的权向量为:

表1 类间目标特征差异实验数据

分析表1 数据，可以看出，不同图像之间统一Hu 矩的差异明显。由于S 越接近0，相似度越高，G1、G2、G3与目标图像的相似度差异在0.05 以上，完全可以将目标图像从其他图像中识别出来。

3.2 类内特征数据分析

采用了图1 的目标图像进行识别实验。每一种基准图像分别以旋转，平移和尺度变换产生3 组图像，共计26 副图像。目标图像经过平移、旋转和尺度变换后相似度检测，得到表2。

表2 目标图像在平移、旋转和尺度变换后的相似度比较

当相似度阈值设定为0.015 时，有5个没有识别出来，识别率为80.76%。当相似度阈值设为0.025 时，26个样本中仅有一个样本没有识别出来，识别率为96.15%。另外，在尺度变换中相似度S值在0.01 以下，具有很好的识别效果，经分析得到是对统一Hu 矩φ3改进后的效果。

3.3 改进前后识别率的比较

为了对比改进后的效果，我们做出下表来进行说明。

在0.025为阈值的条件下的识别度见表3。

表3 阈值为0.025 时的识别百分比

在0.015为阈值的条件下的识别度见表4。

表4 阈值为0.015 时的识别百分比

通过对比可以发现，改进后的算法在图像旋转和尺度变换的识别上有很大幅度的提高，其中尺度变换的矩不变性在实验中很好的表现了出来。

4 结语

本文对离散状态下归一化中心距和统一Hu 矩进行了改进，使得在尺度变换中统一Hu 矩的识别率显著提高，并证明了改进后的统一Hu 矩同样具有区域、边界、离散状态下的不变性。但同时发现了其对于旋转的识别效果仍需提高，所以经过误差分析后提出了权向量的改进方法，大幅度提高了图像经过旋转变换后的识别率，具有更好地应用前景。

［1］丁明跃.不变矩算法研究［J］.数据采集于处理，1992，7(1):1－9.

［2］Chen C C.Improved Moment Invariants for Shape Discrimination［J］.Patten Recognition，1993，26(5):683－686.

［3］杜亚娟，潘泉，张洪才.一种新的不变矩特征在图像识别中的应用［J］.系统工程与电子技术，1999，21(10):71－74.

［4］王波涛，孙景鳌，蔡安妮.相对矩及在几何形状识别中的应用［J］.中国图像图形学报，2001，6(3):296－300.

［5］徐学强，汪渤，贺鹏.统一Hu 矩及在电视图像目标识别中的应用［J］.计算机工程与应用，2006，29:213－214.

［6］肖家庆，卢凌，李晟，等.基于矩不变量的图像识别［J］.武汉理工大学学报，2006，30(4):696－699.

［7］柳林霞，陈杰，窦丽华.不变矩理论及其在目标识别中的应用［J］.火力与指挥控制，2003，28(2):13－14.

［8］程波，杨阳，沈田双.一种基于不变矩和SVM 的图像目标识别方法［J］.仪器仪表学报，2006，27(6):2093－2093.