一个具有调幅特性的分段线性混沌系统与微控制器实现*

朱 雷 ，刘艳云

(1.江苏技术师范学院电气信息工程学院，江苏 常州 213001;2.常州纺织服装职业技术学院机电工程系，江苏 常州 213164)

混沌信号内在的类随机性、对初始条件的极端敏感性等特点使其在信息加密和保密通信［1-3］等领域具有良好的工程应用前景，因此长期以来对于混沌系统的研究成为非线性科学的研究热点［4-5］。从第1个三维连续自治混沌系统即Lorenz 系统［6］被发现开始，研究者对于混沌系统构建的目标主要集中于系统状态方程的代数形式和乘积项、平方项等二次非线性项的设置，而对于分段线性混沌系统的报道较少。文献［7-9］分别报道了两类分段线性Lorenz 系统，改造后的系统中以分段线性项取代原系统中的二次项，却同样具有蝴蝶状混沌吸引子的拓扑结构和丰富的动力学行为。类似地，文献［10］则报道了一类分段线性Chen 系统。从系统的物理实现角度看，一方面，分段线性化后使得混沌系统更容易通过模拟电路实现，另一方面，在以基于微控制器的数字方式实现时，同样可以大幅度提升系统的工作效率。众所周知，在数据处理中，影响微控制器浮点计算效率的关键是乘法计算量，相对于二次项的计算，采用绝对值函数、符号函数等对系统分段线性化后可以使计算量大幅减小。由此可见，对于分段线性混沌系统的构建和实现是一项具有重要意义的工作。文献［11］在Sprott-B 混沌系统［12］模型的基础上提出了一个分段线性Sprott 系统并给出了相应的模拟电路实现结果。本文则在此基础上，提出一种全新的分段线性混沌系统，研究发现，新系统中的常数控制器对于混沌振荡具有线性调幅特性。此外，在采用改进的Euler 算法对新系统进行离散化后，通过16 bit 微控制器MSP430F249 对系统进行了物理实现，实验观察到了新分段线性系统生成的混沌吸引子。

1 分段线性混沌系统模型

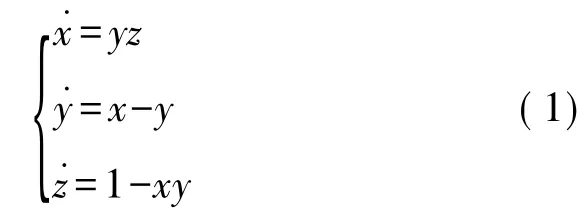
文献［12］提出的三维二次连续Sprott-B 混沌系统可表示为:系统(1)式(1)具有两个对称的鞍焦平衡点并表现出一个两翼蝴蝶混沌吸引子。文献［11］在系统(1)的基础上，将其乘积项yz和xy 分别变为sgn(y)z和sgn(y)y，引入系统参数后提出一个分段线性Sprott系统，这里sgn(·)为符号函数。本文则在此研究基础上，将系统(1)第1个方程的乘积项yz 变为sgn(y)z，第3个方程的xy 项变为|x|+|y|，并引入常数控制器，从而构建出一个分段线性混沌系统(2)，其数学模型为式(2)所示。

式中a和b为系统参数，c为常数控制器，且a，b，c＞0，x，y，z为系统的状态变量。当取典型参数a=1，b=1，c=1 时，系统的相轨图呈现为一个两翼蝴蝶混沌吸引子，如图1所示。

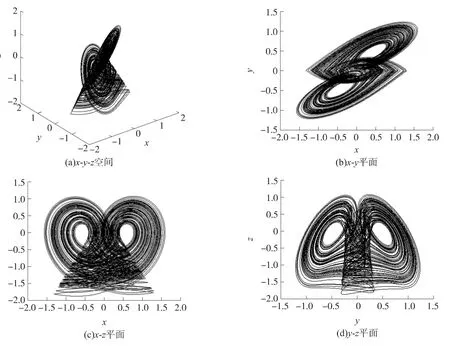
图1 系统(2)的混沌吸引子

2 系统的动力学分析

2.1 基本动力学分析

对于系统(2)，容易验证，在变换(x，y，z)→(-x，-y，z)下具有不变性，故系统关于z 轴对称，且满足

因b ＞0，所以系统(2)是耗散的。代数计算可得系统(2)的两个平衡点分别为Q1=(c/2，c/2，0)和Q2=(-c/2，-c/2，0)，在平衡点Q1和Q2线性化系统(2)，得其Jacobi 矩阵:

计算可得Q1和Q2具有相同的特征多项式:

根据Routh-Hurwitz 判据，平衡点Q1和Q2均不稳定，可能导致系统混沌。当参数a=1，b=1 时，数值计算可知Q1和Q2对应的特征根均为λ1=-1.353 2，λ2，3=0.176 6±1.202 8i，均为指标2 的鞍焦点。

2.2 分岔图分析

固定参数b=1，c=1，当a∈［0.1，10］时，设定(x，y，z)初值为(1，1，0)，仿真可得系统(2)的分岔图，如图2所示。这里x-a 分岔图选择的Poincaré截面为z=0 平面。通过对图2 的观察，结合更为细致的相轨图仿真，可以发现，当0.1≤a≤0.3 时，系统处于弱混沌或拟周期状态，当0.3＜a≤10 时，系统进入鲁棒混沌状态。

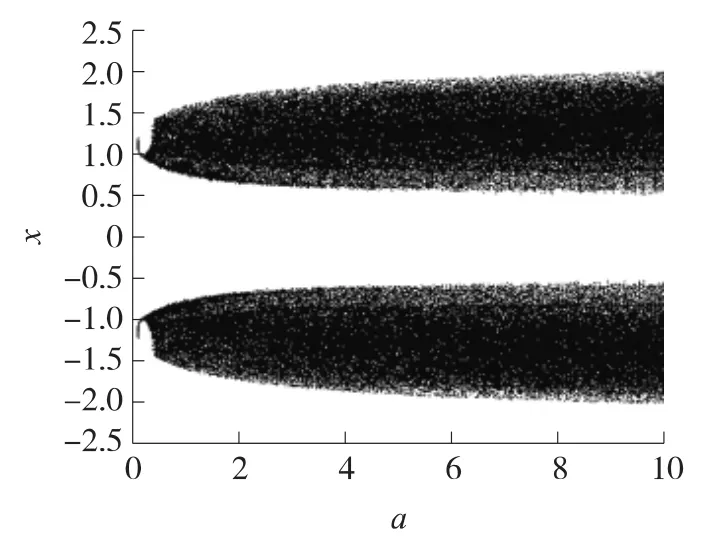
图2 a 变化时系统(2)的x-a 分岔图

固定参数a=1，c=1，当b∈［0.4，10］时，设定(x，y，z)初值为(1，1，0)，仿真可得系统(2)的分岔图，如图3所示。这里x-b 分岔图选择的Poincaré 截面依然

2.3 调幅特性分析

上述分岔图数值仿真已经表明常数控制器c对系统(2)的输出信号x，y和z 的混沌振荡幅度具有线性调幅作用。通过观察Jacobi 矩阵，式(4)，和特征多项式，式(5)可以发现，因c为常数控制器，与平衡点处的特征根无关，所以，c 的变化不会改变系统的混沌特性和吸引子的形状，但会影响系统平衡点的位置，并且伴随c 对混沌振荡的线性调幅作用，平衡点位置在x-y 平面也将发生线性的迁移。下面进一步对c 的全局线性调幅作用进行进一步论证。

定理1 系统常数控制器c 是全局调幅参数，输出信号x，y和z 的幅值与c 呈线性关系变化。

证明 令x=kx*，y=ky*，z=kz*(k ＞0)，则系统(2)变为如下形式:

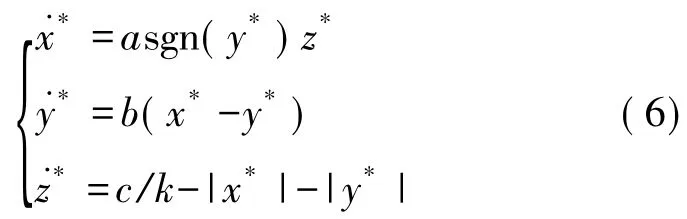
由此可知，c 是全局调幅参数，系统(2)的状态变量x，y和z 的线性调整等价于参数c 的线性尺度变化，即输出信号x，y和z 的幅值与c 呈线性关系是z=0 平面。通过对图3 的观察，结合更为细致的相轨图仿真，可以发现，当0.4≤b≤1.8 时，系统处于混沌状态，当1.8＜b≤10 时，系统处于拟周期或周期状态，且当b≥5.7 时，伴随初值的不同，系统存在有趣的吸引子共存现象。

图3 b 变化时系统(2)的x-b 分岔图

固定参数a=1，b=1，当c∈［0.1，10］时，设定(x，y，z)初值为(0.1，0.1，0)，仿真可得系统(2)的分岔图，如图4所示。这里x-c和y-c 分岔图选择的Poincaré 截面是z=0 平面，而z-c 分岔图选择的Poincaré 截面是随c 动态变化的y=c/2 平面。观察图4 可以清楚地发现，在c∈［0.1，10］的整个参数区间内，系统处于鲁棒混沌状态，且随着c 的增大，系统的输出信号x，y和z 的混沌振荡幅度线性地增加。变化。证毕。

3 微控制器实现与实验验证

在微控制器上进行实验验证前，须首先通过数值计算方法将系统(2)对应的微分方程离散化为差分方程。常用的常微分方程数值计算方法包括Euler 算法、改进的Euler 算法和Runge-Kutta 算法等。在3种算法中，截断误差依次递减，但数值计算时间依次递增。为了兼顾精度和效率，本文采用改进的Euler 算法来进行系统(2)的离散化，于是便有:

式中h为步长，n为迭代次数，且

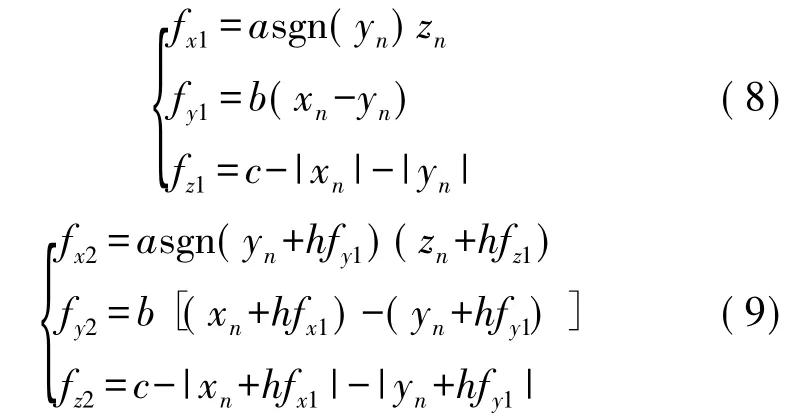
图4 c 变化时系统(2)的分岔图

选择TI 公司著名的16 位低功耗微控制器MSP430F249 实现数字混沌信号的生成，通过Linear Technology 公司的16 bit 高速并行D/A 转换器LTC1668，完成信号转换和输出。采用示波器的XY方式便可观察到系统生成的混沌吸引子。根据式(7)～式(9)编制出相应的C 语言程序，程序中取参数a=1，b=1，c=1，设置(x，y，z)初值为(-1，1，0)，h=0.001，实验过程中采用高分辨率安捷伦DSO7032A 数字示波器进行了观察，结果如图5所示。通过与图1(b)～图1(d)对比可以发现，微控制器运行后生成的混沌吸引子与仿真结果保持一致，证实了微控制器实现本文提出的分段线性混沌系统的可行性。

图5 系统(2)的混沌吸引子实验结果

4 结论

本文通过研究Sprott-B 混沌系统的数学模型，将其两个非线性乘积项变更为分段线性项，并引入系统参数和常数控制器，提出了一个分段线性混沌系统。在典型参数下，系统具有两个指标2 的鞍焦平衡点，从而呈现出一个两翼蝴蝶混沌吸引子。分岔图分析则清晰地表明，参数a 的增加使系统从弱混沌或拟周期状态迅速进入鲁棒混沌状态，参数b 的增加使系统从混沌状态逐渐进入拟周期或周期状态，而常数控制器c 的增加不影响系统的鲁棒混沌状态，却能对系统输出信号起全局线性调幅作用，进一步的理论分析则证明了这一点，这对于混沌在保密通信等领域的应用具有重要的参考价值。在此基础上，通过微控制器MSP430F249 对系统进行了物理实现和相应的实验验证，实验过程中采用改进的Euler 算法对系统方程进行离散化处理，基于C 语言编程，实现并验证了本文所提出的分段线性混沌系统。

［1］Chang W D.Digital Secure Communication via Chaotic Systems［J］.Digital Signal Processing，2009，19(4):693-699.

［2］周武杰，禹思敏.基于现场可编程门阵列技术的混沌数字通信系统——设计与实现［J］.物理学报，2009，58(1):113-119.

［3］Pan J，Ding Q，Du B.A New Improved Scheme of Chaotic Masking Secure Communication Based on Lorenz System［J］.International Journal of Bifurcation and Chaos，2012，22(5):1250125.

［4］Zhang C X，Yu S M，Chen G R.Design and Implementation of Compound Chaotic Attractors ［J］.International Journal of Bifurcation and Chaos，2012，22(5):1250120.

［5］周小勇.一个新混沌系统及其电路仿真［J］.物理学报，2012，61(3):030504.

［6］Lorenz E N.Deterministic Nonperiodic Flows［J］.Journal of the Atmospheric Sciences，1963，20(2):130-141.

［7］Elwakil A S，Kennedy M P.Construction of Classes of Circuit-Independent Chaotic Oscillators Using Passive-Only Nonlinear Devices［J］.IEEE Transactions on Circuits and Systems—Ⅰ:Fundamental Theory and Applications，2001，48(3):289-307.

［8］Lü J H，Chen G R，Yu Y G.Asymptotic Analysis of a Modified Lorenz System［J］.Chinese Physics Letters，2002，19(9):1260-1263.

［9］Elwakil A S，Özoguz S，Kennedy M P.Creation of a Complex Butterfly Attractor Using a Novel Lorenz-Type System［J］.IEEE Transactions on Circuits and Systems—Ⅰ:Fundamental Theory and Applications，2002，49(4):527-530.

［10］Aziz-Alaoui M A，Chen G R.Asymptotic Analysis of a New Piecewise-Linear Chaotic System［J］.International Journal of Bifurcation and Chaos，2002，12(1):147-157.

［11］陈建军，禹思敏.一个分段Sprott 系统及其混沌机理分析［J］.物理学报，2009，58(11):7525-7531.

［12］Sprott J C.Some Simple Chaotic Flows［J］.Physical Review E，1994，50(2):647-650.