驼峰调车场连挂区纵断面优化设计研究*

张春民，李引珍，何瑞春，杨信丰

(兰州交通大学交通运输学院，甘肃 兰州 730070)

在驼峰调车场连挂区，车辆的溜行状态决定着安全连挂率以及天窗产生的数量，超速连挂和天窗对于驼峰调车作业均是不利的，对驼峰作业的安全、效率和能力影响很大［1］。而连挂区的设计合理与否则直接关系到车辆的溜行状态。因此，研究连挂区纵断面的优化设计具有实用价值和现实意义。目前，我国驼峰设计规范中对于连挂区坡段坡度设计的规定是通过统计分析现有22个调车场线路纵断面的数据而得来［2］。对于坡度给出了取值范围，而对于坡长的选取没有明确给出，这使得在实际设计中存在一定困难。由于这几年对调车场连挂区纵断面设计的研究较少［3－4］，大多数研究集中在调速设备的设置方面［5－8］，因而，连挂区纵断面设计存在的问题一直延续至今。本文从车辆溜行状态和投资2个方面来综合考虑连挂区纵断面的设计，研究合理的坡度方案以及与坡长的最佳匹配关系。

1 优化模型

1.1 目标函数

连挂区纵断面的设计需考虑两方面的要求:一是保证车辆良好的溜行状态，二是投资少。本文选择了影响投资费用的2个指标即连挂区计算高度与理想高度的差值最小和减速顶数量最少，以及反映车辆溜行状态的指标难行车溜行距离最远作为目标函数，建立连挂区纵断面优化模型。

1.1.1 减速顶数量

设E制为减速顶的单位制动功(kN·m);lj和ij分别为连挂区各坡段的长度(m)和坡度(%);Q为易行车质量;R易为易行车单位总阻力(N/kN)。设连挂区有m个坡段，则第j个坡段需要的减速顶数量 N 为［9］:

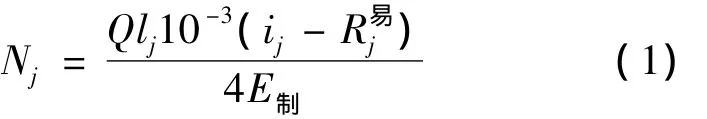
最少的减速顶总数为:

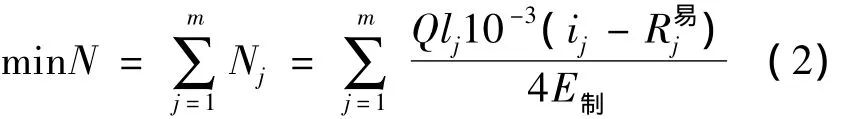
1.1.2 难行车溜行距离

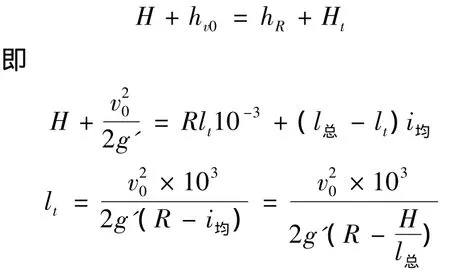
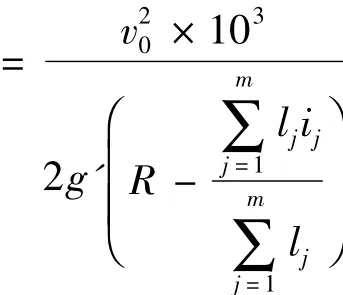
因此，可得到难行车最大溜行距离:

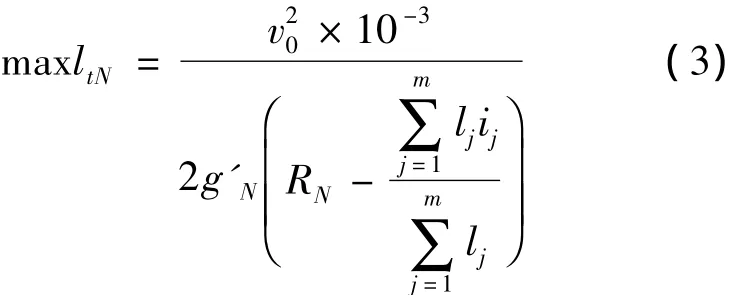
1.1.3 连挂区高度差

连挂区的理想高度以冬季不利溜放条件下的中行车基本阻力当量坡为计算条件［10］，既保证大部分车辆能以不高于安全连挂速度持续溜行，又可以减少工程投资。因此，这里考虑各方案连挂区的计算高度与理想高度的差值越小越好，可表示如下:

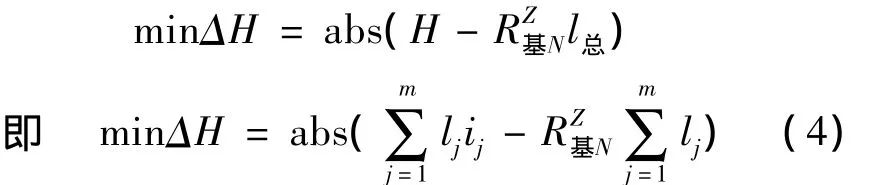
1.2 约束及分析

从运营条件来说，连挂区纵断面设计应满足以下2个约束。

1.2.1 坡段数约束

连挂区应设计成多坡段。在高度相同的条件下，多坡段纵断面的运营条件要优于单一坡段纵断面［2，9］，即 m ＞ 1 ，m 为整数。

1.2.2 坡度约束

根据车辆动力学可知，坡度和阻力之间的关系影响着车辆的溜行状态。为使得连挂区的设计既能满足车辆溜行速度的要求，又能减少投资费用，坡度i的选取考虑选择某一种计算车辆的总阻力当量坡。

溜车条件有溜车有利条件和溜车不利条件2种，坡度可以选择6个当量坡:溜车不利条件难行车的单位总阻力，溜车不利条件中行车的单位总阻力溜车不利条件易行车的单位总阻力，溜车有利条件中行车的单位总阻力，溜车有利条件易行车的单位总阻力和零坡。

⑥i=0，即坡度选用零坡。此时，所有车辆均是减速运行。因此，有:

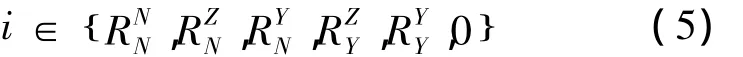
易知①，②，③，④，⑤和⑥中的当量坡的坡度是依次减小的。

另外，根据摆线原理，相邻坡段的坡度成递减趋势解体效率最高。即

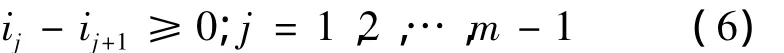
1.3 模型构建

综上所述，可得连挂区纵断面优化模型:

该模型为1个多目标优化问题，可以求其pareto解集，由决策者在实际应用时根据具体情况选用其中的解。这里，通过无量纲化处理和目标权重归一化处理，使其转化成单目标优化问题求解。目标值中有求最大值和最小值，因此，可采用以下方法处理。

对极大化目标:

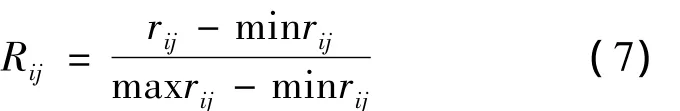
对极小化目标:

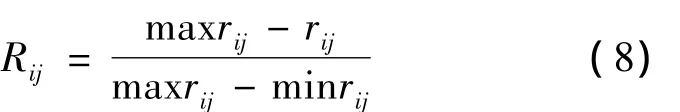
总目标函数为:

其中，wi为权重，i=1，2，3，且w1+w2+w3=1;Fj为第j个坡度组合方案的总目标函数值;Rij为第i个目标函数的第j个坡度组合方案经过无量纲化处理得到的目标值;rij为第i个目标函数的第j个坡度组合方案目标值;maxrij和minrij分别为rij的最大值和最小值。

2 计算分析

通过对模型分析可知，约束条件具有离散组合优化的特点，因此，将先确定坡度的组合集合，而后采用分析比选方法寻求问题的最优解。

2.1 坡度组合集合

通常连挂区一般设计成3～4个坡段。为了计算简单，这里，只分析3个坡段的情况，即m=3。依据坡度约束条件，选择20个坡度组合方案作为备选方案，形成组合集合，如表1所示。

2.2 算法设计

为方便分析问题，模型中涉及的参数需要给定数据，选取西北地区某一路网性编组站驼峰设计时的部分资料，溜车不利条件:t=－2.1℃，vf=4.0m/s，β =9.3°;溜车有利条件:t=27 ℃，β =0°，vf=0 m/s;车场内车辆平均溜放速度为1.4 m/s;设连挂区设计长度为600 m。连挂区内车辆溜行受到的单位总阻力包括基本阻力和风阻力，计算公式可以参考铁路驼峰及调车场设计规范［2］。两种溜放条件下5种阻力当量坡见表2。

算法的主要思路如下:首先选择一个坡长的比例关系，设αs=l1∶l2∶l3，计算在该坡长比例关系下坡度组合方案的总目标函数值F。改变坡长比例关系αs，重复上面计算过程，直到其中某一坡段长度达到最短长度50 m左右时为止。

计算总目标函数时涉及到3个子目标N，ltN和ΔH的权重选取问题，可以采用专家调查法确定。代表驼峰作业效率、安全和工程投资的目标函数主要是难行车溜行的距离和连挂区的高度差，而减速顶设置的目的是在保证解体效率和投资少的基础上，控制易行车速度使得其在安全连挂速度范围内。因此，这里采用难行车溜行距离的权重为0.35，连挂区高度差的权重为0.35，减速顶数量的权重取为0.3。几种情况下的计算结果如表3～6所示。其中:将第一坡段l1增长，第二坡段l2增长和第三坡段l3增长的坡长比例方案分别称为第一类、第二类和第三类坡长方案。表5中只列出了这三种坡长方案下坡度组合方案3的目标函数值，表4所示只列出了第一类和第三类坡长方案下的部分坡长比例关系目标函数值。

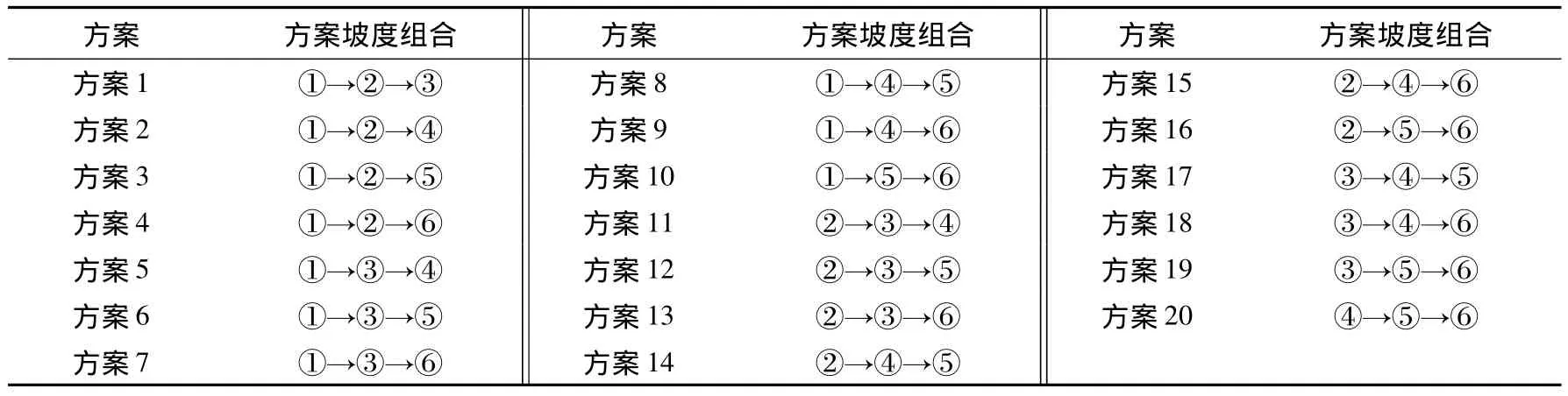
表1 连挂区三坡段设计坡度组合集合Table 1 The combined set of designed gradient with three designed slopes in coupling section

表2 2种溜放条件下5种阻力当量坡计算表结果Table 2 Calculated values of the equivalent gradient of five kinds of resistance in two types of humping operation

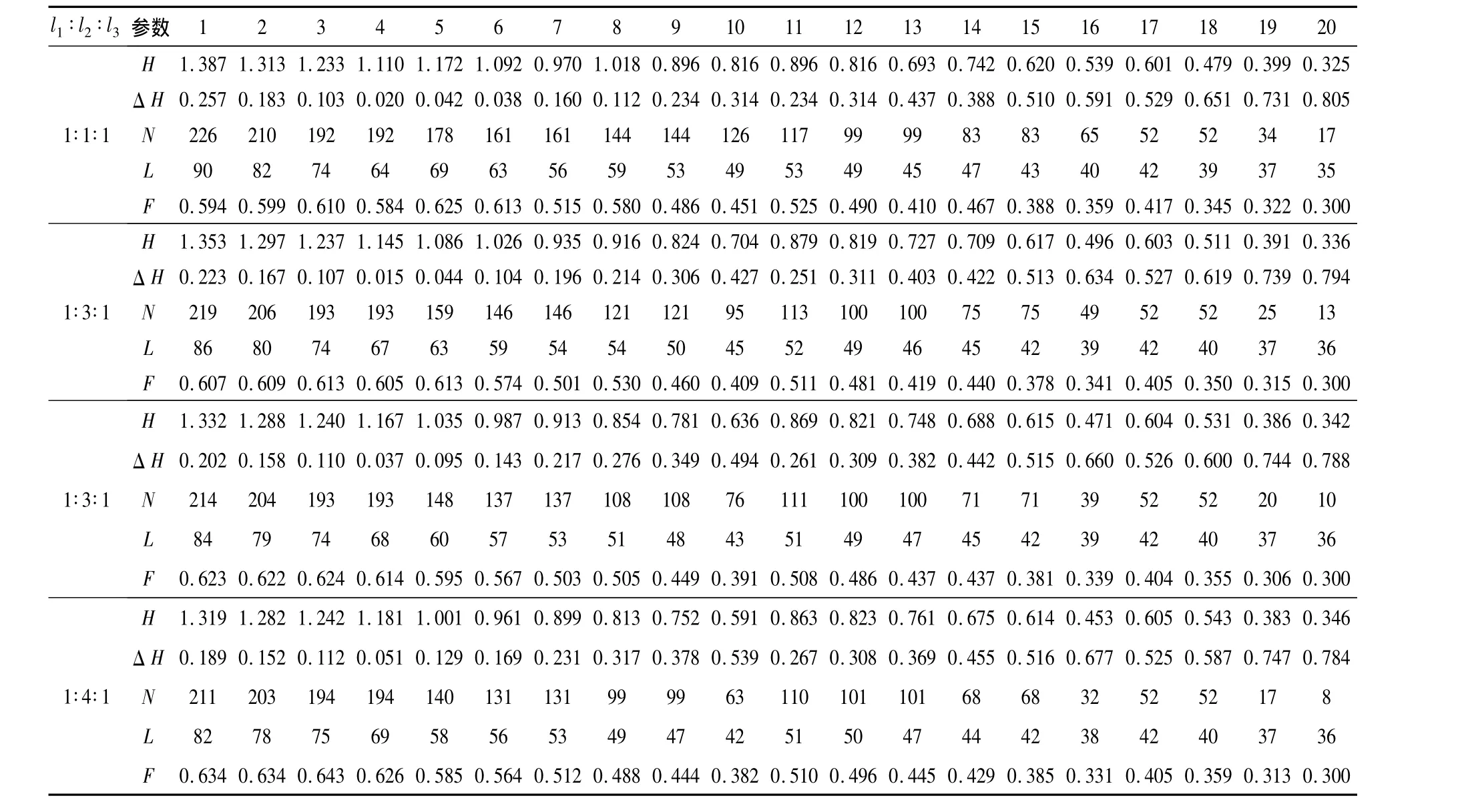
表3 第二类坡长方案中各坡度组合方案的目标函数计算值Table 3 The objective function values of gradient combination schemes for the 2nd slope length scheme

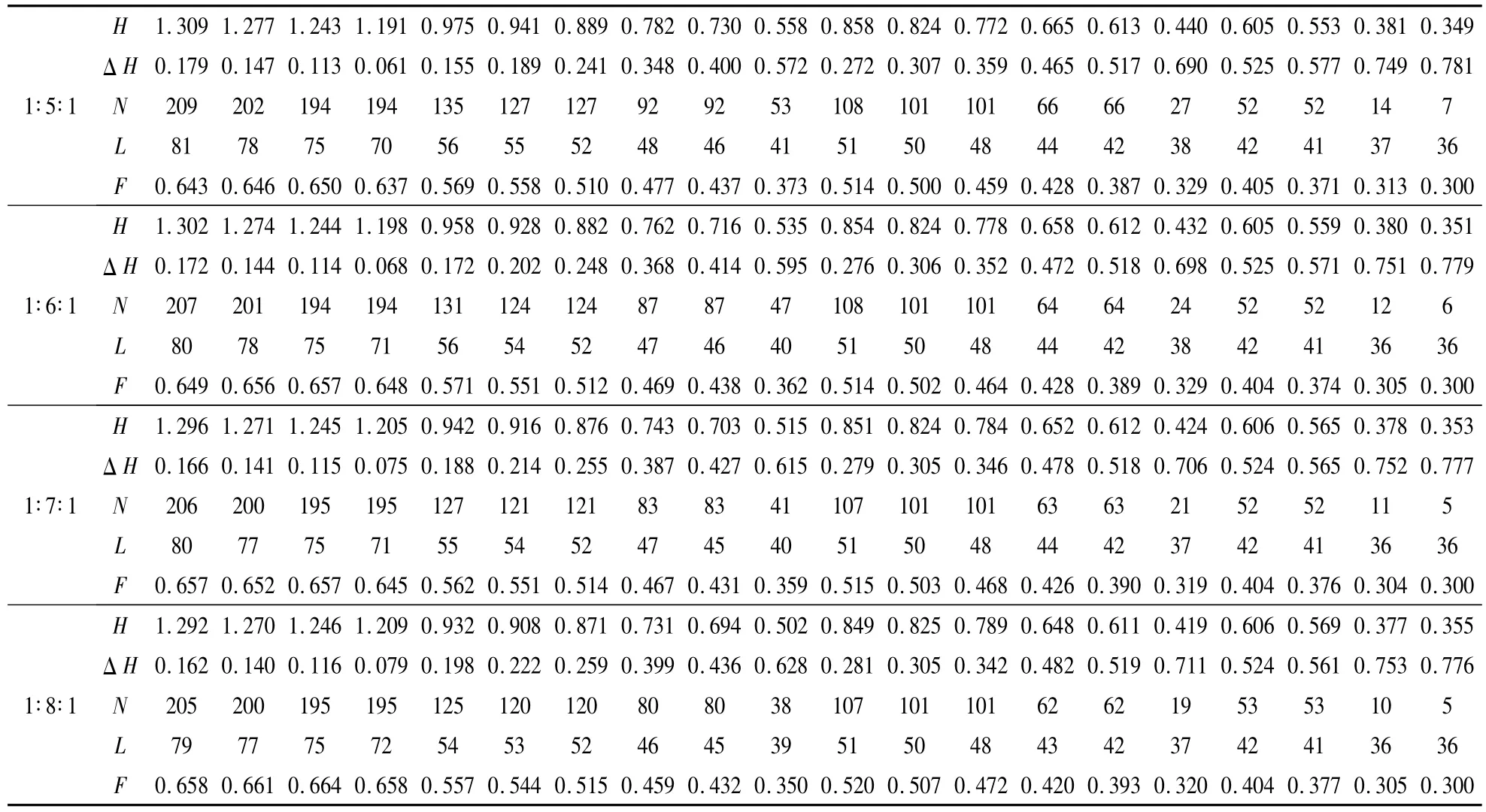
续表3

表4 第一类和第三类坡长方案中各坡度组合方案的目标函数计算值Table 4 The objective function values of both gradient combination schemes for the 1st and 3rd slope length schemes

表5 3种坡长方案比选中坡度组合方案3的目标函数值Table 5 The objective function values of 3rd gradient combination scheme by comparing the three slope length schemes

2.3 计算结果分析

2.3.1 最优坡长方案

(1)从表3和表4可知:第一类坡长方案的连挂区高度和减速顶数量以及难行车溜行距离最大，第三类最小。以坡度组合方案3为例，第一类坡长方案，若 l1∶l2∶l3=2∶1∶1，则高度 H 为1.444 m，难行车溜行距离l为99 m，减速顶N为239个;第二类坡长方案，若 l1∶l2∶l3=1∶2∶1，则高度 H 为1.237 m，难行车溜行距离 l为74 m，减速顶 N为193 个;第三类坡长方案，若 l1∶l2∶l3=1∶1∶2，则高度H为0.98 m，难行车溜行距离l为57 m，减速顶N为144个。这说明:从投资和作业效率2个方面比较，第一类方案均最高，第二类方案次之，第三类方案均最小。可见:坡长方案的选择直接影响着连挂区纵断面的设计合理程度。

(2)从表5可知:3类坡长方案中，第二类坡长方案的总目标函数值F最大。因此，最佳坡长方案可以选择第二类坡长方案，即为第二坡段坡长增大的方案。

2.3.2 最优坡度组合方案

这里分析最优坡长方案即第二类坡长方案下的各坡度组合备选方案。从表3可知:不论设计的三个坡段采用哪种坡长比例设计，总目标函数F最大的为方案3。因此，可以选择方案3作为最优坡度方案，为:①→②→⑤，即第一坡段坡度采用冬季不利溜放条件下的难行车的总阻力当量坡;第二坡段坡度采用冬季不利溜放条件下的中行车的总阻力当量坡;第三坡段坡度采用夏季有利溜放条件下的易行车的总阻力当量坡。

2.3.3 最佳坡长比例关系

(1)坡长对3个目标函数的影响。从表3可知:随着设计的第二坡段逐渐加长，连挂区的高度，减速顶的数量和难行车溜行距离没有太大变化，如高度相差约有0.1 m，减速顶数量相差约10个，难行车溜行距离相差约10 m。但是，在坡长比值一定的条件下，不同的坡度组合方案其减速顶数量和难行车溜行长度以及高度均相差很大，如高度相差1 m，减速顶数量相差约200个，难行车溜行距离相差约40 m。这说明在第二类坡长方案下，各坡段的长度对3个目标函数没有大的影响，影响的主要因素是坡段的坡度值。

(2)最佳坡长比例方案。从表6可知目标函数F较优的2个坡长比例方案为:

l1∶l2∶l3=1∶1∶1，车辆经过前 2 个坡段的溜行，可以溜到连挂区的2/3处;

l1∶l2∶l3=1∶4∶1，车辆经过前 2 个坡段的溜行，可以接近溜到连挂区的末端。

在进行具体坡段的坡长设计时，可以考虑选择上面2个方案。

2.3.4 连挂区纵断面最优方案

由以上分析可得连挂区的合理坡度和坡长最佳匹配方案，见图1。坡度可以采用如下坡度:即第一坡段坡度采用冬季不利溜放条件下的难行车的总阻力当量坡，第二坡段坡度采用冬季不利溜放条件下中行车的总阻力当量坡，第三坡段坡度值采用夏季有利溜放条件下易行车的总阻力当量坡。

坡长采用第二坡段坡长增大的方案，在此基础上，各坡段坡长最佳比例关系可以选择以下2种设计方案:第一方案，3个坡段的坡长相同，各约占连挂区总长的 1/3，即 l1∶l2∶l3=1∶1∶1;第二方案，第一坡段和第三坡段长度相同，第二坡段为其他坡段长度的4 倍，即 l1∶l2∶l3=1∶4∶1。

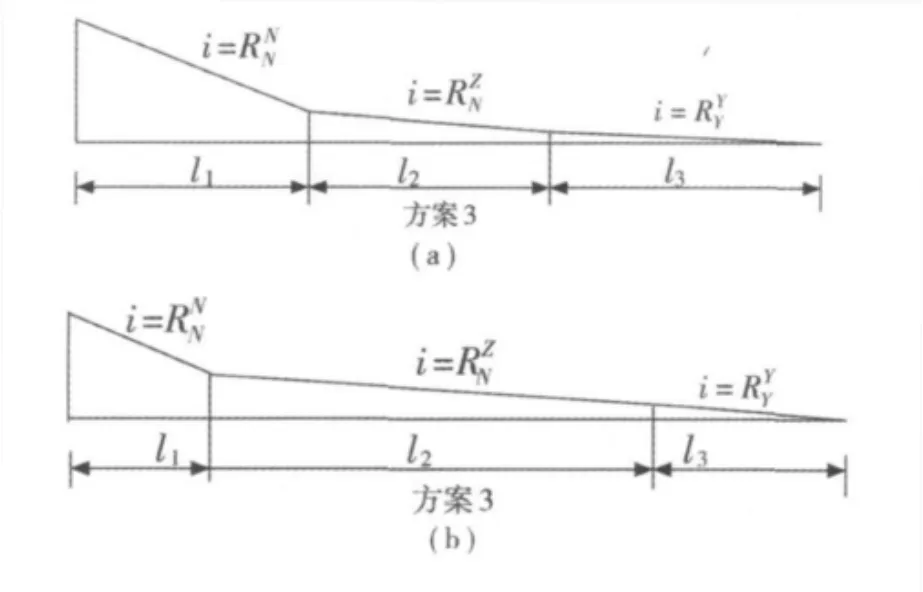
图1 最佳坡度和坡长比例匹配方案Fig.1 the optimal matching scheme between gradient and slope length

3 结论

本文通过分析连挂区纵断面设计对车辆的溜行状态以及投资2个方面的影响，建立了连挂区纵断面的多目标优化模型，并根据模型特点设计了求解问题的算法;通过对可能的坡度组合以及坡长方案的比选分析，确定了合理的坡度组合方案和最佳的坡段长度比例关系，为驼峰连挂区的科学设计提供一定的理论依据。

［1］张春民，李引珍，陈志忠，等.基于贝叶斯网络的驼峰超速连挂事故分析［J］.铁道学报.2011，33(10):7－13.ZHANG Chun-min，LI Yin-zhen，CHEN Zhi-zhong，et al.Analysis on over－speed coupling accidents on hump based on bayesian network［J］.Journal of the China Railway Society.2011，33(10):7 －13.

［2］TB10062—99，铁路驼峰及调车场设计规范［M］.TB10062—99，Code for design of railway station and terminal［M］.

［3］高玺华.关于驼峰调车场合理坡度及减速器控制长度的初探［J］.减速顶及调速技术，2001(1):6－8.GAO Xi-hua.Initial Exploration on rational grade and controlling length of clasp retarders of hump yard［J］.Retarders and Speed Control Technology，2001(1):6 －8.

［4］周国平，高玺华.点式控制自动化调车场设计坡度的优化［J］.减速顶及调速技术，2010(1):6－7.ZHOU Guo-ping，GAO Xi-hua.Optimizing the design grade in automation marshalling yard of“Point”type control system［J］.Retarders and Speed Control Technology，2010(1):6－7.

［5］张 环.变速打靶条件下连挂区布顶设计的探讨［J］.减速顶及调速技术，2005(1):21－22.ZHANG Huan.Exploration on design of retarder layout in coupling area under condition of retardation to target with variable velocity［J］.Retarders and Speed Control Technology，2005(1):21 －22.

［6］钟 楠，孙士臣.关于简易驼峰调车场减速顶调速系统设计的新思考［J］.减速顶及调速技术，2003(1):1－4.ZHONG Nan，SUN Shi-chen.New think on design of speed control system of retard for simplified hump shunt ing yard［J］.Retarders and Speed Control Technology，2003(1):1－4.

［7］谢立宏.适应重载货车的点连式调速系统布顶探讨［J］.铁道运输与经济，2008，30(4):93 －94.XIE Li-hong.Exploration of the retarders layout of point and continuous speed control system to adapt to heavy haul freight cars［J］.Railway Transport and Economy，2008，30(4):93－94.

［8］余文利.重载与减速顶调速系统［J］.减速顶及调速技术，2010(1):11－13.YU Wen-li.Retarder speed control system with over －loading translation［J］.Retarders and Speed Control Technology，2010(1):11 －13.

［9］刘其滨，马桂珍.铁路车站及枢纽［M］.北京:中国铁道出版社，2002.LIU Qi-bin，MA Gui-zhen.Railway station and terminal［M］.Beijing:China Railway Publishing House，2002.

［10］祝庆增，向劲松.点连式驼峰优化设计［J］.铁道学报，1990，3(12):16 －27.ZHU Qing-zeng，XIANG Jin-song.Optimum hump design incorporating target－shooting and continuous regulation system［J］.Journal of the China Railway Society，1990，3(12):16－27.

［11］张红亮.基于货车大型化的驼峰设计与作业控制理论研究［D］.北京:北京交通大学，2010.ZHANG Hong-liang.Hump design and operation control under large－size car developing condition［D］.Beijing:Beijing Jiaotong University，2010.