应用于智能微网的SVPWM固态变压器研究

张明锐 刘金辉 金 鑫

（同济大学电子与信息工程学院 上海 200092）

1 引言

为了解决人类所面临的能源危机，大规模利用分布式能源和可再生能源发电，一种新的电网运行模式——微型电网近年来在国外发展十分迅速。未来可再生电能传输和管理（Future Renewable Electric Energy Delivery and Management，FREEDM）网络，是由美国北卡州立大学提出的新型智能微型电网模型，目前正在兴建 1MW的试验性示范电网。它由美国国家科学基金会自2008年起开始资助，此外，还联合了其他若干著名大学和跨国企业共同研究[1]。

FREEDM是一个革命性的绿色低碳电力网络，它基于高带宽数字通信、分布式控制和电力电子器件。在结构上，它是一个特殊的微型环形网络，回路由电缆或传输线连接，电压设计为10kV，与本地供电系统并网的电压可为35kV或110kV（美国这两项数据分别为12.47kV、69kV）。各种可再生分布式电源、储能设备和负载通过固态变压器（Solid State Transformer，SST）提供的接口接入系统。分布式电源可以采用太阳能光伏电池、风力发电机、燃料电池和微型燃气轮机等。储能设备包括蓄电池、超级电容等，用于维持网络中的功率平衡，实现负荷的削峰填谷。各电源、储能设备和负载之间并联。FREEDM既可以并入当地主电网运行，也可以与主电网解列孤岛运行。

在FREEDM中，SST用于替代传统的工频变压器。与传统变压器相比，SST通过电力电子变换技术实现电力系统中电压变换和能量传递，具有体积小、重量轻、空载损耗小、不需要绝缘油等优点[2]。它不仅具有变压功能，而且兼具限制故障电流、平衡有功功率、改善电能质量以及为各种设备提供标准化接口等多种功能。由SST提供的四象限功率控制允许分布式发电设备即插即用，任意将储能设施和负载接入FREEDM而不影响附近其他用户，为用户提供高品质的供电。电能在SST中可以双向流动，因此FREEDM中电能的流动可以是多向的，它是一个能源的因特网，每个电力用户不仅是能源的消费者，也是能源的供应者。用户可以根据自身的需求将分布式电源产生的多余电能卖回给电力公司[3]。

SST是 FREEDM 的核心设备。目前国外对FREEDM和SST的研究尚处于起步阶段，国内尚未见其他单位对 FREEDM 予以关注，本文引进FREEDM的先进设计理念，对应用于FREEDM的SST进行研究。主要从SST的拓扑结构、功能实现及控制方法几个方面加以分析，并建立一个基于我国电网参数的三相SST模型用于仿真研究。

2 固态变压器的原理与FREEDM

2.1 固态变压器的原理及发展

在变压器中，可推导出下述关系式:

式中，B为变压器的磁通密度；Ac为铁心面积；N为绕组匝数。由式（1）可见，当磁通密度一定时，Ac与工作频率f成反比，这样如果提高变压器的工作频率就可提高铁心的利用率，大幅减小变压器的体积并提高其整体效率。因此减小变压器的体积是固态变压器早期的主要研究目标。美国海军在1980年提出了SST的雏形[4]。文献报道，传统的2.7MVA工频变压器重量超过6t，而同样容量的SST重量只有原来的1/3左右[5]。

国内对固态变压器的研究在 FREEDM 出现之前就已经开始。早期的研究，主要从输配电变压器的角度展开，文献表明，SST在降低变压器体积与重量，稳定输出电压方面有显著优势[6]。文献[7]对固态变压器在输电系统中的应用进行了研究，结果表明固态变压器在改善输电系统电压特性，提高系统的阻尼和稳定性方面具有显著效果。FREEDM的提出，为SST的研究注入了新的活力。

根据固态变压器中是否存在直流单元，SST的拓扑结构分为两大类:一种是在电力电子变压器中不存在直流单元，称为直接交-交型SST；另一种是在电力电子变压器中包含直流单元，称为交-直-交型SST。应用于FREEDM的SST需要较复杂控制功能，交-直-交型更加适合。

2.2 固态变压器在FREEDM中的运行模式

在FREEDM中，SST的运行模式由其所配置的分布式电源、储能装置和负载的运行工况决定。从FREEDM运行控制的角度，可以将SST的运行模式归为两大类:P-Q模式和V-S模式。

（1）P-Q模式。P-Q模式也称之为负载模式。按照P-Q模式运行的SST，向电网输送或从电网吸收功率，SST与电网同步，此时的SST对配置的分布式电源和储能装置没有特殊要求，甚至可以只配置负载。

（2）V-S（Voltage Source）模式。V-S模式，也称为电压源模式。在FREEDM联网运行时，其功能与P-Q模式类似。在FREEDM进入孤岛运行模式时，承担稳定环网电压和频率的作用，此时的 SST必须配置足够容量、响应快速的分布式电源或储能装置。

在FREEDM联网运行时，电压和频率由外部电网限定，SST没有稳定频率、电压的要求，主要实现分布式电源的经济运行和执行电网的功率调节指令，SST的两种运行模式都可以满足。在FREEDM孤岛运行时，其所含的SST必须有部分或者全部按照V-S模式运行，来稳定FREEDM环网的频率和电压，换言之，如果SST不具备V-S模式的运行功能，FREEDM将无法孤岛运行。

SST不管处于以上哪种运行模式，都可以实现与外网的双向电能流动。

将SST应用于FREEDM，需要十分复杂的控制功能，本文针对 FREEDM联网模式下SST的功能进行研究。孤岛模式下的SST控制性能将另行研究。

3 固态变压器的拓扑结构

图1是一个典型的三相交-直-交型SST拓扑结构。该结构由输入侧三相全控整流器、中间DC-DC直流变换单元和输出侧三相全控逆变器三部分组成，其中，中间 DC-DC直流变换单元又由一个单相全桥逆变器、高频变压器和一个单相全桥整流器三部分组成。高压工频交流输入首先通过输入AC-DC整流器变换为高压直流电；再通过一个单相全桥变换器被调制成高频高压交流电，然后通过高频变压器降压变换为高频低压交流电，该低压交流电经单相全控整流器被还原为直流；最后经过输出DC-AC逆变单元变换为所需的低压工频交流输出。

在当前电力电子器件耐压受限的情况下，必须采用多个开关器件串联使用，并且解决开关器件串联使用时所带来的均压和可靠性问题。为了在现有条件下解决上述问题，E.R.Ronan和S.D.Sudhoff等人提出了一种由输入级（高压级）、隔离级和输出级（低压级）组成的三阶式 SST[8]。其特点在于输入级采用多级功率模块串联，高压侧输入电压被均分到每一模块上，从而可减小高压侧单个功率模块上所承受的电压，各模块内部可不必串联。输入级各模块为单位功率因数整流器。

对配电系统而言，一次侧电压等级高，二次侧电压等级低，那么在容量一定的情况下，势必会出现一次侧电流小，而二次侧电流大。为此，可以采用一种输入侧串联、输出侧并联的大容量SST实现方案。其特点是，通过输入模块的串联提高了输入电压等级，通过输出模块的并联提高了输出电流等级。非常适用于高压大功率应用场合。图2用单相SST结构说明这种方案的串并联连接方式。

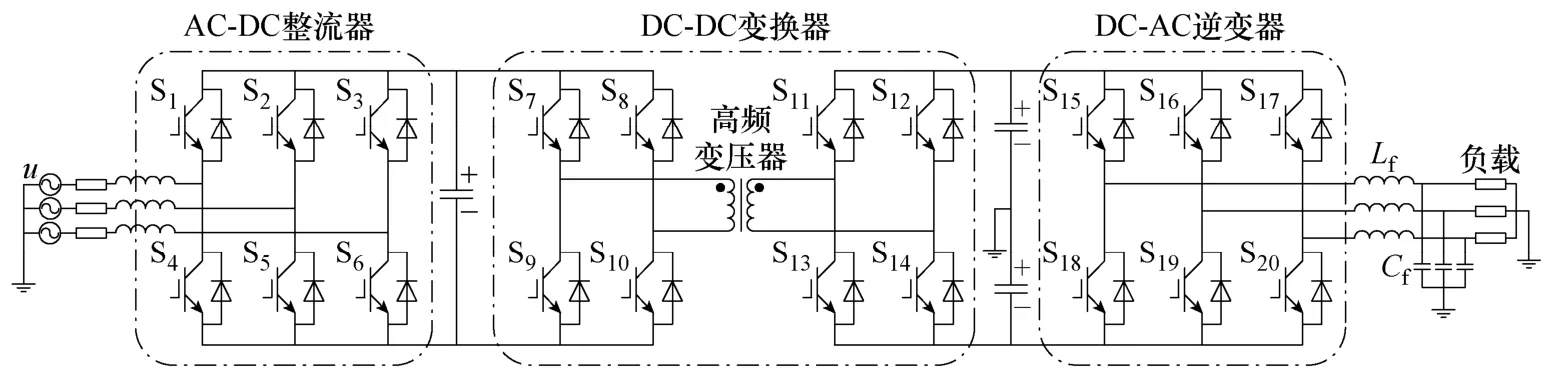
图1 三相SST的基本拓扑结构图Fig.1 The basic topology of three-phase SST

图2 高压侧串联低压侧并联的SSTFig.2 High voltage modules in series and low voltage connection in parallel

4 固态变压器的功能实现

在 FREEDM 中，从电网角度看，通过采用合适的控制策略，SST需要实现以下功能目标:①输出电压控制为恒定的工频正弦交流电压，能有效抵抗电网电压扰动和负载扰动；②无功功率补偿，SST能在优先满足负载有功功率需求的情况下根据设定的功率因数目标向电网注入或吸收无功电流，最好是单位输入功率因数；③过电流保护和欠电压保护。本文以三相交-直-交型SST为例，对输入整流单元、中间DC-DC变换单元和输出逆变单元三部分的功能和控制方式分别加以讨论。单相SST的实现方法与此类似，但进行单相DQ电流解耦控制时需要引入相应的虚拟电量[9]。

4.1 空间电压矢量调制技术SVPWM

相对于传统的 PWM控制，SVPWM控制利用空间电压矢量的切换以获得准圆形旋转磁场，从而在不高的开关频率(1～3kHz)条件下，获得更好的控制性能，SVPWM提高了电压型整流器和逆变器的电压利用率，而且其简单的矢量模式切换易于微处理器的实现[10]。

空间电压矢量控制用三相电压矢量去逼近矢量电压圆，输入端会得到等效三相正弦电压波形。三相变流器空间电压矢量共有8个，除2个零矢量外，其余6个非零矢量对称均匀分布在复平面上，如图3所示。对任一给定的空间电压矢量Ur，均可由相邻的两个基本电压矢量和零电压矢量来合成。

图3 电压空间矢量合成图Fig.3 The basic voltage space vectors

空间电压矢量合成的计算步骤如下:

（1）判断参考电压矢量所在扇区，选择参与矢量合成的基本空间矢量。

（2）计算每个空间矢量的作用时间（占空比）。

（3）确定空间矢量序列。

4.1.1 判断参考电压矢量所在扇区

把电压矢量从三相坐标系转换到两相静止坐标系，由克拉克变换（abc/αβ变换）有

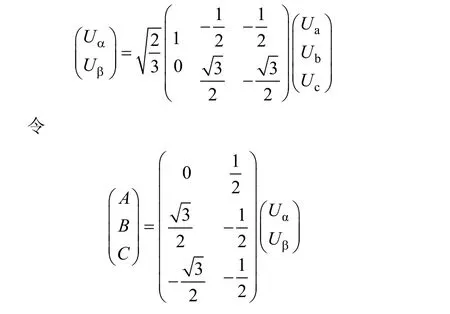
引入符号函数sign(x)，设N=sign(A)+2sign(B)+4sign(C)，这里N 对应着6个扇区。经过计算，可以得出N 和扇区之间对应关系见表1[11]。

表1 N值与对应的扇区号Tab.1 Sector based on N

4.1.2 空间矢量的作用时间

如图3所示，以参考矢量Ur位于扇区Ⅰ为例，选择邻近的空间矢量 U1和 U2以及零矢量 U0来合成，则有

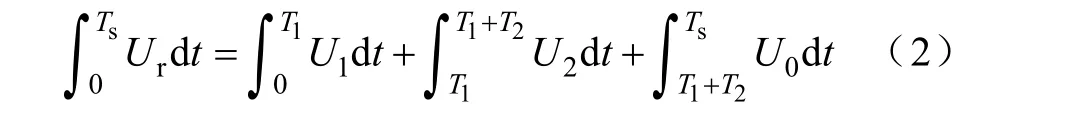
若开关频率比电压型变流器交流侧的基波频率高得多，则可以近似认为 U1在一个开关周期 Ts中恒定，上式简化为

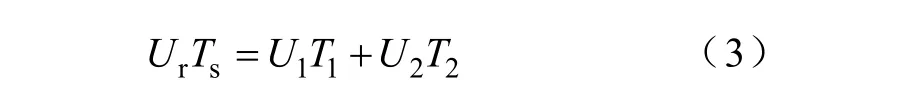
由正弦定律可以解得

式中，m为 SVPWM 调制系数。根据 T1、T2和开关的切换规则，并考虑到扇区的不同，可计算出开关作用时间 Ton1、Ton2、Ton3。将 Ton1、Ton2、Ton3作为调制波，三角波作为载波，比较即可得到SVPWM的输出脉冲[12]。

4.2 输入整流单元

如图1所示，三相SST的输入单元是一个三相全控整流器。建立其在dq旋转坐标系下的简化数学模型，对于三相交流对称系统，忽略开关过程中的高频分量，稳态时dq模型的d、q分量均为直流变量；若取d轴与电网电动势矢量同向，则按照瞬时无功功率理论，d轴表示有功分量，q轴表示无功分量，只需要令q轴电流参考量i*q=0，即可实现单位输入功率因数。整流器采用电压、电流双闭环 PI调节器控制，电压外环的作用主要是控制输出直流电压，保证直流电压的恒定；电流内环的作用主要是按照电压外环输出的电流指令进行电流控制，实现单位功率因数。

DQ旋转坐标系下电压型SVPWM整流器的简化数学模型可以表示为[13]

式中，p为微分算子；ud、uq为电网输入电压的d、q分量；urd、urq为整流器交流侧输入电压的 d、q分量；id、iq为整流器交流侧输入电流的d、q分量。

由式（4）可知, d轴电流和q轴电流之间存在耦合，在 d轴控制回路中增加一项:ωLiq，它刚好抵消d轴等效电路模型中来自q轴的影响；对q轴电流控制器进行同样改造，即可实现d轴电流回路和q轴电流回路的解耦控制。为了提高系统的抗干扰能力和动态性能，把电网电压作为前馈补偿，于是得到SVPWM整流器的双环解耦控制框图如图4所示。

图4 SST输入SVPWM整流单元解耦控制框图Fig.4 d-q decoupled controller of SST SVPWM rectifier

4.3 中间DC-DC变换单元

中间 DC-DC变换单元由单相全桥逆变电路、高频隔离变压器和单相桥式全控整流电路组成。由SST整流单元输出的高压直流电首先通过逆变器调制成高频方波，再通过高频变压器耦合到二次侧，最后通过一个由同步信号控制的整流器还原成低压直流。其中的逆变器和整流器均采用 PWM控制，驱动信号为占空比为50%的互补触发脉冲。高频变压器主要起电气隔离和电压等级变换的作用。DCDC单元在结构上完全对称，从而允许电能双向传输。此外，可以增加软开关电路实现零电压开通和零电流关断，提高工作频率，减少开关损耗。

当一次侧逆变器与二次侧整流器的触发脉冲不同步，存在相角差时，有[14]

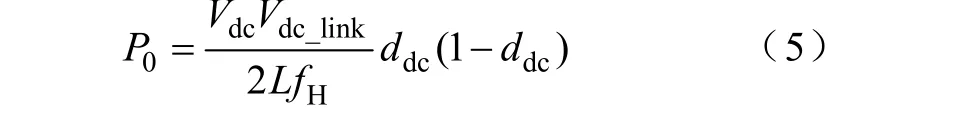
式中，P0为DC-DC单元传输的有功功率；Vdc为高压侧输入直流电压；fH为开关频率；L为漏感；Vdc_link为低压侧输出直流电压；ddc为一次、二次调制信号的移相角差。

中间 DC-DC单元的控制目标是输出恒定的低压直流电。由式（5）可以看出，通过控制移相角差ddc，即可控制低压侧输出直流电压Vdc_link，为此引入无静差的PI调节器控制即可。

除了以上的控制策略，中间 DC-DC单元的核心技术是高频变压器的研制，而磁性材料又是高频变压器研究的关键所在。目前，开发高性能的纳米超微晶合金材料是该领域的热门研究内容，也是高频变压器工程化的希望所在。

4.4 输出逆变单元

如图1所示，三相SST的输出单元由三相半桥逆变器和 LC滤波器组成，其功能为输出恒定幅值的三相工频正弦交流电。三相半桥电路采用中性点引出接线，三相之间没有耦合关系，每一相都是独立的，可以看成是三个输出电压相位互差 120°的单相半桥逆变器的组合，因此可以应用单相逆变器的控制方法。

为了保证输出波形的有效值精度，本文采用电压瞬时值控制，在瞬时值内环外面再加一个平均值环对输出波形的幅值进行调整。内环通过瞬时值控制获得快速的动态性能，保证输出畸变率较低，外环通过输出电压的平均值控制，具有较高的输出精度[15]。其控制框图如图 5所示。图中输出电压 Vo经整流滤波后得到直流量与给定参考信号的有效值进行比较，得到的误差信号经外环调节器后的输出作为内环参考正弦波的幅值，这个幅值与单位正弦波相乘后作为内环给定信号。内环给定信号与输出电压瞬时值比较，得到的误差信号经 PI调节器运算，作为内环的控制信号送入SVPWM发生器。

图5 SST输出SVPWM逆变单元控制框图Fig.5 Controller of SST SVPWM inverter

5 仿真实验与波形

根据我国电力系统的电压等级，FREEDM环网的额定线电压设计为10kV，在Matlab2007b/Simulink环境下，根据图1搭建一个三相交-直-交SST模型，并进行仿真。SST电网侧输入为线电压UL=10kV、f=50Hz的三相正弦交流电，负载侧输出为线电压380V的三相工频正弦交流电。其他主要参数为:SST输入侧的等值电阻 R=0.5Ω，电感 L=10mH，SVPWM 开关频率 fs=10kHz，直流侧支撑电容C=4700μF，直流输出电压为 Vdc=15.5kV；中间DC-DC变换单元高频变压器的一次电压为15.5kV，二次电压为600V，工作频率为 5kHz；SST输出逆变单元的滤波电感L=80μH，滤波电容C=880μF，SST的设计容量约为2.7MVA。相对于采用PWM控制的SST[16]，采用SVPWM控制后，SST直流环节的电压降低了约15%。在SST高压侧交流电压等级不变的条件下，高压侧直流环节电压的适当降低，在目前功率开关器件耐压受限的情况下，降低了SST的工程化难度[17]。有关仿真波形如图6～图8所示。

图6 SST a相输入电压和电流波形Fig.6 Input voltage and current of phase a

图7 SST整流单元直流输出电压波形Fig.7 Output DC voltage of SST rectifier

图8 SST交流输出线电压波形Fig.8 Output AC voltage of SST

由图6可以看出，在经过约0.15s调整后，SST输入交流电压、电流波形基本保持同相，FREEDM电网侧输入功率因数恒定为 1。由图 7可以看出，SST输入整流单元的输出直流电压在经过短暂的过渡过程后稳定在15.5kV。由图8可以看出，SST的输出三相交流线电压在经过约 0.15s调整后保持为三相对称正弦交流波形，有效值约为380V。将SST所接负载由2.7MW切换为1.4MW时，仿真所得波形基本保持不变，可见SST对负载扰动具有良好的抗干扰性。

为缩短过渡过程时间，以下仿真中将输入直流侧的电容电压初值设置为15.5kV。当SST接感性负载（有功负载P=2.5MW，无功负载QL=0.5Mvar）时，可得仿真波形如图9和图10所示。

图9 阻感负载时SST输入电压电流a相波形Fig.9 Input voltage and current of phase a with RL load

图10 阻感负载时SST交流输出线电压波形Fig.10 Output AC voltage of SST with RL load

由图9可以看出，在经过短暂过渡过程之后，SST的输入交流电压和电流基本保持同相，输入侧功率因数为1，可见SST具有无功补偿功能。由图10可以看出，SST的输出电压波形保持为三相正弦交流，有效值约为380V。

为了仿真逆功率输送，即将分布式电源产生的能量从低压侧传输到高压侧然后送往电网，同时保证SST按照额定容量工作，使用6MW的受控电源，其中3MW供低压负载使用，3MW逆向送往电网。仿真波形如图11和图12所示。

图11 带分布式电源时SST a相输入电压和电流波形Fig.11 Input voltage and current of phase a with DG

图12 带分布式电源时SST交流输出线电压波形Fig.12 Output AC voltage of SST with DG

由图11可以看出，在经过短暂过渡过程之后，SST的输入交流电压和电流基本保持反相，输入侧功率因数为-1，即SST向电网输出有功功率，由此可见 SST可以双向传输电能，能够根据需要向FREEDM注入有功功率。由图 12可以看出，SST的输出电压波形保持为三相正弦交流，有效值约为380V。由以上仿真分析可见，本文设计的SST基本实现了FREEDM所要求的控制目标。

6 结论

综上所述，本文对新型智能微型电网FREEDM的核心设备SST进行了研究，分析了其工作原理、拓扑结构和控制策略，根据我国电力系统电压等级的参数，设计了一个采用SVPWM控制技术的三相SST模型，通过仿真验证了该设计方案的有效性，为将FREEDM的先进理念引入我国、开发中国化的FREEDM电网奠定了基础。由于我国常用配电电压等级高达10kV，而现在商用IGBT模块的最高电压等级一般在6.5kV左右，因此必须采用串联分压和并联分流来弥补功率器件的不足。但最根本的方案还是要研究利用高能隙带的SiC、GaN等新材料制造新一代的电力电子器件[18]。相对Si来说，SiC的击穿电压高10倍，散热性更好，本征载流子浓度更低，有望将SST的效率提高到接近100%。由于SST中存在的非线性、复杂性、时变性和不确定性等，很难得到精确的数学模型，导致采用传统的PI调节器控制很难得到满意的结果，因此可以考虑将智能控制理论中的专家控制、模糊控制等引入SST的控制，保证系统的跟随性能，提高SST的鲁棒性和自适应性。在我国目前正如火如荼进行的智能电网建设和新能源开发利用中，FREEDM及其核心设备固态变压器大有可为，应用前景广阔。

[1]Huang Alex Q.Renewable energy system research and education at the NSF FREEDM systems center[C].2009 IEEE Power and Energy Society General Meeting, Calgary, AB, Canada, 2009, 7: 1-6.

[2]Ronan E R, Sudhoff S D, Glover S F, et al.Application of power electronics to the distribution transformer[C].Proceedings of the 15th Annual IEEE Applied Power Electronics Conference and Exposition,New Orleans, LA, 2000, 2: 861-867.

[3]Huang A Q, Baliga J.FREEDM system: role of power electronics and power semiconductors[C].Proceedings of the 21st International Symposium on Power Semiconductor Devices & IC's, Barcelona, 2009, 6:9-12.

[4]Brooks J L.Solid state transformer concept development [M].Naval Material Command, Civil Engineering Laboratory, Naval Construction Battalion Ctr., Port Hueneme, CA, 1980.

[5]Jun Wang, Huang A, Woongje Sung, et al.Smart grid technologies[J].IEEE Industrial Electronics Magazine,2009, 3(2): 16-23.

[6]王丹, 毛承雄, 陆继明.自平衡电子电力变压器[J].中国电机工程学报, 2007, 27 (6): 77-83.Wang Dan, Mao Chengxiong, Lu Jiming.Autobalancing electronic power transformer[J].Proceedings of the CSEE, 2007, 27(6): 77-83.

[7]曹解围, 毛承雄, 陆继明, 等.电力电子变压器在改善电力系统动态特性中的应用[J].电力自动化设备, 2005, 25(4): 65-68.Cao Jiewei, Mao Chengxiong, Lu Jiming, et al.Improving power system dynamic characteristics with power electronic transformer[J].Electric Power Automation Equipment, 2005, 25(4): 65-68.

[8]Ronan E R, Sudhoff S D, Glover S F, et al.A power electronic-based distribution transformer[J].IEEE Transactions on Power Delivery, 2002, 17 (2):537-543.

[9]Miranda U A, Aredes M, Rolim L G B.A DQ synchronous reference frame current control for single-phase converters[C].IEEE 36th Power Electronics Specialists Conference, 2005, 6: 1377-1381.

[10]郑强.电力电子变压器的新型拓扑结构和智能控制研究[D].武汉: 武汉理工大学, 2007.

[11]马耀辉, 尹华杰, 汪万维.三相电压型PWM整流器空间电压矢量控制仿真[J].防爆电机, 2009, 44(2):15-18.Ma Yaohui, Yin Huajie, Wang Wanwei.The simulation of three phase voltage PWM rectifier adopting SVPWM control strategy[J].Explosion Proof Motor, 2009, 44(2): 15-18.

[12]王宇, 熊光煜, 王淑红.三相 PWM 整流/逆变器的建模与仿真[J].电气技术, 2010(1): 33-36.Wang Yu, Xiong Guangyu, Wang Shuhong.The modeling and simulation of three phase PWM rectifier and inverter[J].Electrical Technology,2010(1): 33-36.

[13]张崇巍, 张兴.PWM整流器及其控制[M].北京: 机械工业出版社, 2002.

[14]Tiefu Zhao, Jie Zeng, Bhattacharya S, et al.An average model of solid state transformer for dynamic system simulation[C].IEEE Power & Energy Society General Meeting, Calgary, AB, 2009, 7: 1-8.

[15]徐德鸿.电力电子系统建模及控制[M].北京: 机械工业出版社, 2006.

[16]刘金辉, 张明锐, 金鑫.应用于新型微网 FREEDM的固态变压器研究[J].电气自动化, 2010, 32(6):48-53.Liu Jinhui, Zhang Mingrui, Jin Xin.Research on the solid state transformer applied in FREEDM microgrid[J].Electrical Automation, 2010, 32(6):48-53.

[17]刘金辉.FREEDM中的固态变压器及其对继电保护的影响[D].上海: 同济大学, 2011.

[18]Woongje Sung, Jun Wang, Huang A Q, et al.Design and investigation of frequency capability of 15kV 4H-SiC IGBT[C]. Proceedings of the 21st International Symposium on Power Semiconductor Devices & IC's, Barcelona, 2009, 6: 271-274.