三相T型滤波并网逆变电源的网侧电流直接控制技术
2012-08-07胡雪峰龚春英章家岩
胡雪峰 龚春英 陈 新 章家岩
(1.南京航空航天大学航空电源重点实验室 南京 2100162.安徽工业大学电力电子与运动控制省重点实验室 马鞍山 243002)
1 引言
近年来,由于化石能源的逐渐枯竭,全球电力系统正面临着巨大的变革,基于风能、太阳能等新能源分布式发电和微电网技术的提出都为未来电力系统的发展指明了方向,其中并网逆变电源是新能源发电领域中的关键接口装置[1-5],研究其结构和控制策略对于改善新能源并网发电质量,提高发电效率,进而推动可再生能源的合理开发和利用具有重要的理论意义和应用价值。
衡量新能源并网发电电能质量的重要指标主要有两个方面,即溃入电网电流的功率因数及其总谐波失真度。为了平滑溃入电网电流的波形质量,通常把单个电感串联在逆变电源的输出端与电网之间起到滤波的功能,即L型滤波器。这种滤波器的优点是结构简单、易于控制,其缺点是L型滤波器对高频谐波仅能以20dB/dec的速度进行衰减,衰减的速度特性不够理想,通常需要较大的电感量才能对开关次数谐波进行有效衰减,或者需要采用较高的开关频率以提高谐波频率,进而可采用合适的电感量,但是,电感量增大会增加装置体积,提高发电系统的成本,影响系统的动态响应等。如果开关频率过高,无疑会增大系统的损耗,降低发电效率。而 T型滤波器是三阶滤波器,它可以以 60dB/dec的速度对谐波进行衰减,要达到相同的滤波效果,T型滤波器的总电感量相比L型滤波器要小得多,不但可以减小发电装置的体积和重量,降低新能源发电的成本,而且有利于提高系统的动态特性。因此,T型滤波器已被广泛应用于 PWM并网变换器中,并有取代单L型滤波器的趋势。但是T型滤波器也有其自身的局限性,由于它的串入提高了并网逆变电源的阶数,如果控制策略不当,将会引起系统振荡,这对采取何种控制策略提出了更高的要求。文献[6-7]证明了仅采用网侧电流单环控制的T型滤波并网逆变电源系统是不稳定的,文献[6]采用控制逆变电源侧电感电流来间接控制馈网电流取得了满意效果,文献[8]提出在电容端串联阻尼电阻来抑制谐振,有效抑制了系统不稳定现象的发生。
本文针对三相T型滤波并网逆变电源提出了同步旋转坐标系下的网侧电流作为外环,以取得单位功率因数馈网电流,提高直接馈网电流的控制精度;采用同步旋转坐标系下的滤波电容电流作为内环以增加系统阻尼,抑制谐振发生,降低馈网电流谐波含量的新型控制策略。在建立系统线性控制模型的基础上,推出了系统的特征方程,证明了该控制策略的稳定性;给出了滤波器的设计准则;为了确保系统的稳定,推出了滤波器参数L1、L2、C取值的大小与控制器参数取值的关系。仿真和实验结果都验证了该控制策略的有效性和可行性。
2 系统的状态空间建模及其稳定性分析
2.1 系统的整体结构
三相T型滤波并网逆变电源系统的原理框图如图1所示。其中可再生能源提供单向流动的直流电压,逆变环节采用三相全桥变换器,经T型滤波环节接至公共电网,直接通过调节输出电流IL2实现馈网发电。

图1 三相T型滤波并网逆变电源发电系统结构图Fig.1 Proposed system of 3 phase grid-connected inverter
2.2 三相T型滤波并网逆变电源系统的状态空间模型
为了便于分析,首先作如下假设:①三相电网电压对称且稳定;②忽略滤波电感和电容的ESR,忽略直流母线电压的波动;③电路的开关器件为理想开关元件,无死区因素的影响。这样当开关频率远高于输出滤波器的截止频率时,三相全桥逆变桥可以看作一个增益环节kPWM。分别选择电感L1中的电流 i1K,电感 L2中的电流 i2K和滤波电容电压VCK为状态变量,设逆变桥环节输出端至中性点的电压分别为VKN,三相电网电压分别为VSK,其中,K=a,b,c,则逆变电源功率级的的状态方程为


由上述状态方程式可知,三相状态变量(di1a/dt di2a/dt dvca/dt)T,(di1b/dt di2b/dt dvcb/dt)T和(di1c/dt di2c/dt dvcc/dt)T之间没有任何耦合关系。并且其形式与单相逆变器的状态方程是一致的。因此,该逆变电源系统的控制策略及其稳定性的讨论可以基于单相逆变器展开,把上述状态方程变换到复频域可得到三相 T型滤波并网逆变电源的状态空间模型为


2.3 系统的控制策略及其稳定性分析
国内外学者针对T型滤波并网逆变器的运行提出了一些相应的控制方案[9-11],总体上可以分为直接电流控制和间接电流控制。其中直接电流控制又分为控制逆变器侧电感电流(Inverter Side Current Control,ISCC)和控制网侧电感电流(Grid Side Current Control,GSCC)两类。其中采用ISCC控制逆变器侧电感电流的方案,采用单环控制,且能确保系统的稳定性,取得了较好的效果,但该方法毕竟不是直接控制馈入电网的电流,其控制精度和馈网电流的功率因数都不易精确控制,文献[4,12]研究了滤波电容串联阻尼电阻后,采用直接控制网侧电流的方案,给出了该方案下若干个有实际意义的结论。本文提出采用基于旋转坐标系的网侧电流作为直接控制外环,和基于旋转坐标系的滤波电容电流作为内环的直流变量控制策略。由式(4)~式(6)可知,采用 T型滤波的三相并网逆变电源,各相的馈网电流是相互独立的,即对于三相平衡系统而言,如果控制策略针对每一相馈网电流单独控制时是稳定的,则采用坐标变换后,再利用该控制策略同样是稳定的,这是因为坐标变换是基于功率能量等效进行的,只是能量表示方法的不同而已,并不影响其稳定性,所以只要在A,B,C三相坐标系下的稳定并网系统,变换到两相旋转坐标系下并采用同样的控制策略仍然是稳定的。
如果对于图1中逆变电源系统的每一相在A,B,C坐标下采用网侧电流直接单环控制,则系统是不稳定的[8],本文引入滤波电容电流作为网侧电流控制环的内环,主要用来消除馈网电流中开关频率谐波分量可能引起的谐振,以增强系统的稳定性,且不需串联耗能电阻,其控制原理框图如图 2a所示。图中 G1(s)=Kp+Ki/s,G2(s)=K,G3(s)=KPWM,G4(s)=1/(sL1),G5(s)=1/(sC),G6(s)=1/(sL2)。因为图 2a中引入滤波电容电流环的作用是增加系统的稳定性,所以其控制器只需用比例控制即可,比例系数为 K。为方便看出网侧电流直接控制的传函,利用控制框图的等效变换法对图2a进行等效变换,因为i2K是被控量(K=a,b,c),所以只能按i2K引出点不变的规则进行变换后,进一步化简得到采用网侧电流直接控制的等效结构框图如图2b所示。根据图2b可知,馈网电流的质量不但与直接电流控制策略有关,还受到电网电压自身谐波含量的影响,本文只讨论前者,则系统的开环传递函数为


图2 带电容电流反馈内环的网侧电流直接控制框图Fig.2 Block diagram of direct grid-current controller with iC feedback inner loop
画出系统的根轨迹曲线如图3所示,可以看出该系统是一个条件稳定系统。

图3 系统的根轨迹图Fig.3 Root locus of direct grid-current control system
为求出系统的稳定条件,由式(7)得到闭环传递函数

列写闭环系统传递函数的特征方程为

由胡尔维茨(Hurwitz)稳定判据得出系统稳定的充要条件为式(9)各项系数全大于零且


稳定性是控制系统的重要性能,是系统正常工作的首要条件,由式(11)可知,要使系统稳定运行,必须处理好各控制器参数和系统自身参数如L1、L2、C等之间的关系,当T型滤波器总电感参数确定后(设计方法见第3节),综合式(10)~式(13)作进一步分析可以得到以下结论:
(1)首先确定L2与L1的比值关系,则控制器G1参数必须满足式(11)和式(12)系统才能确保稳定。
(2)考虑到外环控制器参数对系统的快速性,稳态误差都有很大的影响,所以这种直接并网电流控制方法,也可以首先从控制指标上确定Kp=h,即:假设 L2=(h-1)L1,根据电网对高次谐波电流的要求由谐波的衰减比例求出 h值,再由总电感值L=L1+(h-1)L1分别计算出 L1和 L2,可同比例增大或缩小,注意这里的计算仅是由稳定的边界条件出发,得出的各参数间的理论关系,实验时总电感值或各分电感值可以进行微调。
2.4 系统稳定性与电容及其内环反馈系数的关系
由式(7)可以看出,引入电容电流内环反馈控制后,系统馈网电流的开环传函是一个典Ⅰ系统,也相当于间接配置了系统的极点,其特征阻尼比为
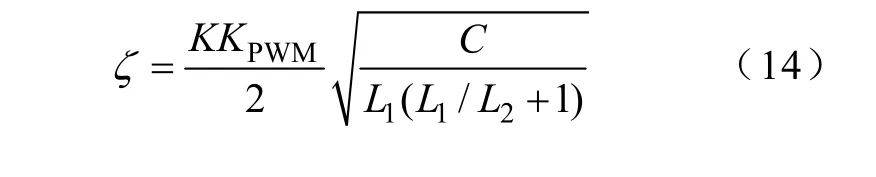
式(14)表明增大电容电流内环反馈控制系数或增大滤波电容值,都可以使系统的阻尼比增大,从而提高抑制系统可能发生谐振的能力,但如果只追求大阻尼,则系统的调节时间就会变长而影响系统的动态响应,为了兼顾系统的阻尼效果和动态响应性能,工程上通常取在最佳阻尼比附近,因此本文在滤波电容确定的情况下,再依据式(14)设计内环的反馈控制系数。

图4 系统阻尼ζ随K和C的变化关系Fig.4 The system damping factor ζ changes with K and C
3 T型滤波器的优化设计
因为滤波器参数影响并网逆变器控制系统的设计,所以进行控制器设计之前必须首先确定滤波器的参数,由于T型滤波器在较低频段时的幅值特性和L型滤波器相近,其中L=L1+L2,所以可先依据单电感滤波器的设计方法计算出总的电感值[4,8],但是综合L型和T型滤波器幅频和相频特性来看,会发现 L型滤波器的相位滞后最大为π/2,而 T型滤波器的相位滞后会随着阻尼系数和工作频率的增加迅速变大,直至3π/2,而且阻尼系数较小时会引起系统的严重谐振现象,即控制系统中阻尼系数较小或较大都是不合适的,所以本文通过以下方式对 T型滤波器进行优化设计:
(1)首先根据式(15)计算总的电感值:

式中,fs为PWM信号的开关频率;fg为馈网电流的基波频率;ih为开关频率处的谐波电流要求Ug为电网电压的峰值;ILp为电感电流的峰值。又因为电感值越小,电流的跟踪能力及系统的响应越快,而电感值越大,滤波效果越好,因此需要根据式(15)综合考虑,选择合适的电感值。
(2)虽然目前有关并网电流谐波标准所关注的是并网接入点的电流谐波,但就并网逆变器本身的设计而言也需要限制逆变器侧电感电流的纹波,如果该纹波过大会使滤波元件的损耗增加,同时使开关管的开关应力升高,所以实际工程中通常要把逆变器的桥臂电流纹波限制在一定的范围之内,又因为逆变器侧电感电流是随开关周期而脉动变化的,所以通过分析一个电网周期中不同时段的电感电流纹波变化规律,从中得出最大电流纹波值,即可得到逆变器侧电感L1的取值约束条件如式(16)。

式中,Δimax为逆变器侧电感允许最大电流纹波幅值;T为逆变器的开关周期。
(3)滤波电容的选取既要考虑对开关频率处谐波电流有较好的分流作用,又要确保系统具有一定的工作频带,在此基础上考虑到电容值越大,产生的无功越多,会造成系统效率下降,所以在满足条件的基础上尽可能取小,如电容产生的无功被限制在不超过5%的系统额定功率,则

(4)由式(14)求出系统在最佳阻尼比时内环控制参数K值。 实际应用中还可以根据仿真与试验来进一步修正和优化参数。
根据上述参数选择原则设计了一台额定容量为6kVA的并网逆变器,其开关频率fs= 20kHz,直流侧输入电压Udc=300V,网侧相电压有效值通过隔离变压器变为Ug=100V,L1= 0.4mH,L2=2.5mH,C=5μF。其中L2考虑了变压器折算到低压侧的漏感,变压器本身可视为理想变压器。
4 仿真分析
利用Matlab/Simulink结合 S函数软件建立基于旋转坐标系下并网逆变电源的数学模型,然后采用旋转坐标dq轴下网侧电流作为外环,旋转坐标dq轴下滤波电容电流作为内环的直接馈网电流控制策略进行了系统仿真,以验证采用本文控制策略时系统的稳定性及动态性能。图5和图6为Kp=5,Ki=0.1时系统馈网电流和电网电压的稳态波形和调制波形。图 7为 Kp=7,超出式(11)所表示的稳定条件时系统发散的波形图,图8和图9分别为Kp=5,Ki=0.1时系统馈网电流由满载到半载和由半载到满载时的动态波形。仿真结果与前面理论分析结果是一致的。

图5 稳态仿真波形(Kp=5, Ki=0.1)Fig.5 Simulation waveform with proposed control strategy (Kp=5, Ki=0.1)

图6 稳态时A,B相调制波仿真波形(Kp=5, Ki =0.1)Fig.6 Simulation of steady state modulation waveform with proposed control strategy (Kp=5, Ki =0.1)

图7 系统处于发散区的仿真波形(Kp=7, Ki=0.1)Fig.7 Simulation waveforms when unstable system (Kp=7, Ki=0.1)

图8 T型滤波并网逆变电源从半载到满载工作的动态仿真波形Fig.8 Simulation waveforms with dynamic response from half load to full load

图9 T型滤波并网逆变器从满载到半载工作的动态仿真波形Fig.9 Simulation waveforms with dynamic response from full load to half load
5 实验验证
为验证上述控制器参数设计的合理性,以微处理器 TMS320F2812为核心控制器件搭建了 T型滤波并网逆变电源的试验样机,直流电压由单相整流桥提供单向能量,采用电压比可调的工频隔离变压器串联在逆变电源系统与电网之间。开关频率为20kHz,开关的死区时间设为 2μs。实验结果如图10~图12所示,图10为并网电流与电网电压的稳态实验波形,利用谐波分析仪测得此时的电流的PF为 0.998,THD为 2.1%;图 11为并网电流突变时的动态实验波形,图12是稳态时A相电流及其调制波的实验波形,从实验结果可以看出,针对T型滤波的并网逆变电源,采用本文所提的控制策略时,既能获得很好的稳态馈网电流波形质量和较高的功率因数,又具有良好的动态性能。

图10 并网电流稳态实验波形Fig.10 Experimental waveforms of grid current

图11 并网电流动态实验波形Fig.11 Experimental waveforms of grid current

图12 稳态时A相电流及其调制波实验波形Fig.12 Experimental waveforms of phase A current and its modulation waveforms with proposed control strategy
6 结论
本文研究了T型滤波并网逆变电源系统的网侧电流直接控制策略,提出了基于dq旋转坐标系的网侧电流作为外环,和基于dq旋转坐标系的电容电流作为内环的SVPWM控制策略,外环采用网侧电流直接控制,实现了并网电流的高功率因数运行,提高了电流的控制精度,降低了并网电流的谐波含量;加入电容电流内环配置了系统的极点,间接增强了系统的阻尼,改善了系统的稳定性。推出了本文所提控制策略的稳定条件,给出了T型滤波器的优化设计准则,以及系统阻尼比与滤波电容及电容电流反馈控制参数之间的定量关系,为T型滤波并网逆变电源的直接电流控制提供了理论依据。仿真和实验结果表明:该控制策略具有优良的稳态和动态性能,验证了本文控制策略参数设计方案的实用性和可行性。
[1]由世俊, 杨洪兴, 娄承芝, 等.建筑物用光伏集成系统在中国应用的前景[J].太阳能学报, 2000,21(4): 434-438.You Shijun, Yang Hongxing, Lou Chengzhi, et al.The prospect of BIPV in China[J].Acta Energiae Solaris Sinica, 2000, 21(4): 434-438.
[2]王长贵.世界光伏发电技术现状和发展趋势[J].新能源, 2000, 22(1): 44-48.Wang Changgui.The present status and the trend of development of the world photovoltaic technology[J].New Energy, 2000, 22(1): 44-48.
[3]赵清林, 郭小强, 邬伟扬.单相逆变器并网控制技术研究[J].中国电机工程学报, 2007, 27(16): 60-64.Zhao Qinglin, Guo Xiaoqiang, Wu Weiyang.Research on control strategy for single-phase grid-connected inverter [J].Proceedings of the CSEE,2007, 27(16): 60-64.
[4]Tirumala R, Mohan N, Henze C.Seamless transfer of grid-connected PWM inverters between utilityinteractive and stand- alone modes[C].IEEE Applied Power Electronics Conference and Exposition, Dallas,USA, 2002.
[5]Lindgren M, Svensson J.Control of a voltage-source converter connected to the grid through an LCL-filter:application to active filtering[C].IEEE Power Electronics Specialists Conference, Fukuoda, Japan,1998.
[6]张强, 张崇巍, 张兴, 等.风力发电用大功率并网逆变器研究[J].中国电机工程学报, 2007, 27(16):55-59.Zhang Qiang, Zhang Chongwei, Zhang Xing, et al.Study on grid-connected inverter used in high-power wind generation system[J].Proceedings of the CSEE,2007, 27(16): 55-59.
[7]Twining, Holmes D G.Grid current regulation of a three-phase voltage source inverter with an LCL input filter[J].IEEE Transactions on Power Electronics,2003, 18(1): 373-380.
[8]张承慧, 叶颖, 陈阿莲, 等.基于输出电流控制的光伏并网逆变电源[J].电工技术学报, 2007, 22(8):41-45.Zhang Chenghui, Ye Ying, Chen Alian, et al.Research on grid-connected photovoltaic inverter based on output current control[J].Transactions of China Electrotechnical Society, 2007, 22(8): 41-45.
[9]Bueno E J, Espinosa F, Rodriguez F J, et al.Current control of voltage source converters connected to the grid through an LCL-filter[C].IEEE Power Electronics Specialists Conference, Aachen, Germany,2004.
[10]蒋燕君, 张超.基于DSP的光伏并网发电系统数字锁相技术[J].电源技术应用, 2007, 10(2): 29-32.Jiang Yanjun, Zhang Chao.Research on digital PLL of the grid-connected PV power generation system based on DSP [J].Power Supply Technologies and Applications, 2007, 10 (2): 29-32.
[11]Serpa L A, Ponnaluri S.A modified direct power control strategy allowing the connection of three-phase inverters to the grid through LCL filters[J].IEEE Transactions on Industry Applications,2007, 43(5): 1388-1400.
[12]郭小强, 邬伟扬, 顾和荣, 等.并网逆变器 LCL接口直接输出电流控制建模及稳定性分析[J].电工技术学报, 2010, 25(3): 102-109.Guo Xiaoqiang, Wu Weiyang, Gu Herong, et al.Modelling and Stability Analysis of direct output current control for LCL interfaced grid-connected inverters[J].Transactions of China Electrotechnical Society, 2010, 25(3): 102-109.
[13]Wu E, Lehn P W.Digital current control of a voltage source converter with active damping of LCL resonance[J]. IEEE Transactions on Power Electronics, 2006, 21(5): 1364-1373.
[14]Liserre M, Teodorescu R, Blaabjerg F.Stability of photovoltaic and wind turbine grid-connected inverters for a large set of grid impedance values,IEEE Transactions on Power Electronics, 2006, 21(3):836-841.
[15]Hea-Gwang Jeong, Kyo-Beum Lee, Sewan Choi,Performance improvement of LCL filter based grid-connected inverters using PQR power transformation[J].IEEE Transactions on Power Electronics, 2010, 25(5): 1320-1330.
[16]Kim D E, Lee D C.Feedback linearization control of grid interactive PWM converters with LCL filters[J].Journal of Power Electronics, 2009, 9(2): 288-299.
[17]Araújo S, Zacharias P.Analysis on the potential of silicon carbide MOSFET and other innovative semiconductor technologies in the photovoltaic branch[C].Proceeding of the 13th Eur.Conf.Power Electron, 2009.
