ABDOM的参数规范化与离散化改进

何智涛 晏海华 刘 超

(北京航空航天大学 计算机学院，北京100191)

软件缺陷发现时序过程的叠加双阻尼振荡模型(ABDOM，Accumulative Bi-Damped Oscillation Model)［1］为软件测试过程的度量和评估提供了一种新的手段.该模型是一个可初步描述软件缺陷发现时序过程的周期性、随机振荡性和阻尼衰减性等基本特征及关键影响因素的数学模型.但是，为了能更好描述复杂的软件缺陷发现场景，当前的ABDOM模型仍然存在需要改进的地方:

1)在现有的ABDOM中，软件缺陷发现阻尼a和软件缺陷发现周期阻尼b的具体意义尚不很明确，而这些参数的物理意义和规范化的取值对于软件测试过程质量的评估和预测有着重要的指导意义.因此，有必要通过进一步的拟合实验分析，对参数a和b的物理意义进行深入探讨，进而讨论参数a和b的规范化取值.

2)同时鉴于在测试工程实践中，测试与开发人员变更、测试周期调整等因素的变化均是非连续的，呈现离散化特征，因此ABDOM中的相关参数需要进行进一步的离散化改进来增强ABDOM对离散变化的适应能力.

3)使用ABDOM模型对实际的软件缺陷发现过程进行预测和评估是建立ABDOM模型的最终目标.因此，基于ABDOM参数规范化研究成果，有必要开展软件缺陷发现过程质量评价因素研究.

本文将围绕以上问题开展研究与实践检验.

1ABDOM模型简述

叠加双阻尼振荡模型ABDOM是一种可在一定条件下描述软件缺陷发现时序过程的数学模型.如式(1)所示:

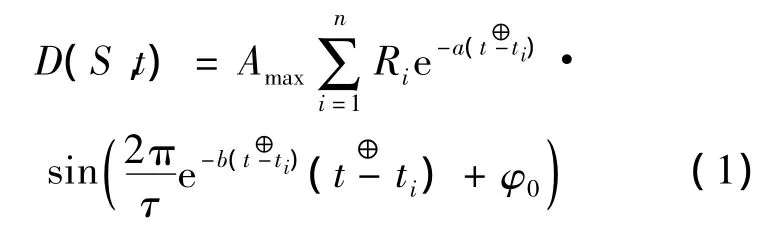
软件缺陷发现时序过程的特性(时序性、周期性、衰减性和振荡性)在ABDOM中得到了较好描述:软件缺陷发现的时序性、周期性和振荡性通过sin(t)函数表达;软件缺陷发现数量和发现周期的衰减特性通过指数函数et表达.

产生软件缺陷发现振荡特性的影响因素(被测软件影响因素、开发过程影响因素和测试过程影响因素)在ABDOM模型中得到反映:Amax，b和τ反映了测试过程影响因素，即Amax描述测试项目组的能力，也侧面反映了软件测试资源状况;τ描述软件缺陷发现周期;b用于描述软件缺陷发现周期的稳定性;Ri描述增量式开发的影响，即新版本引入的代码规模;a描述软件缺陷发现数量衰减率，揭示了被测软件中发现软件缺陷的难易程度和被测软件代码质量的影响，也一定程度反映了软件测试过程的质量.

2ABDOM的参数规范化研究

在ABDOM中，软件缺陷发现阻尼a和软件缺陷发现周期阻尼b的物理意义不很明确，鉴于这些参数对软件测试质量预测和评估的重要指导意义，以下将研究软件缺陷发现阻尼a和软件缺陷发现周期阻尼b的物理意义和规范化.

2.1 理想软件缺陷发现过程范型

由于ABDOM是描述软件缺陷发现时序过程的数学模型，因此要研究ABDOM的参数规范化，就需首先研究软件缺陷发现时序过程的理想范型，通过ABDOM对理想范型的拟合来获取模型参数的实际意义.

目前在国内外软件工程领域内，有较多动态基于时间关系的软件缺陷预测技术成果［2］，如Rayleigh 分布模型［3］、指数分布模型［4］和 S 曲线分布模型［5］等，国内有何智涛等提出的 ABDOM模型和王彤等提出的p阶自回归-q阶移动平均模型(auto regressive moving average):ARMA(p，q)［6］，但这些研究成果中，并没有直接涉及理想状态软件缺陷发现时序范型研究.

这里基于软件缺陷发现时序过程的周期性、振荡性和衰减性特征，借鉴Rayleigh概率分布密度函数(PDF，Probability Density Function)分布模型，结合测试实践经验，提出一个理想软件缺陷发现时序过程(ISPSDD，Ideal Sequential Process of Software Defects Discovery).

定义1 理想软件缺陷发现时序过程(ISPSDD).ISPSDD是一个时序过程.在此时序过程中，软件的开发和测试过程质量均处于理想工作状态，软件缺陷发现周期τ1内发现了待测软件系统中的所有软件缺陷，在后续等长回归测试周期τ2(τ2=τ1)内，不再有新的软件缺陷被发现;且在软件缺陷发现周期τ1内，软件缺陷日发现率呈衰减趋势并在τ1结束时趋近于0.

ISPSDD的范型如图1所示.

图1 ISPSDD范型图示

理想软件缺陷发现时序过程只是一种理想状态，工程实践中是根本无法达到的，从开发过程和测试过程两方面来考虑，有如下表述:

1)若开发过程质量达不到理想状态，即软件缺陷发现周期τ1内被测软件需求覆盖不完整，或开发人员对软件缺陷发现周期τ1内出现的软件缺陷修复不完善，则势必导致回归测试周期τ2内出现新增软件缺陷和周期性振荡;

2)若测试过程质量达不到理想状态，即在软件缺陷发现周期τ1内测试人员未能完整覆盖测试需求，导致部分测试需求在回归测试周期τ2内才被覆盖，也势必导致回归测试过程中出现新增软件缺陷和周期性振荡.

2.2 基于ISPSDD的ABDOM的参数a研究

在定义了ISPSDD后，使用ABDOM来拟合ISPSDD，期望可以发现有指导意义的各参数.

鉴于软件缺陷发现周期τ，测试组织能力Amax都是变化因素，因此在使用ABDOM的拟合测算中，在将Amax指定为一个确定值条件(50，100和200)下，分别代入不同的软件缺陷发现周期.最终的拟合测算结果如表1所示.

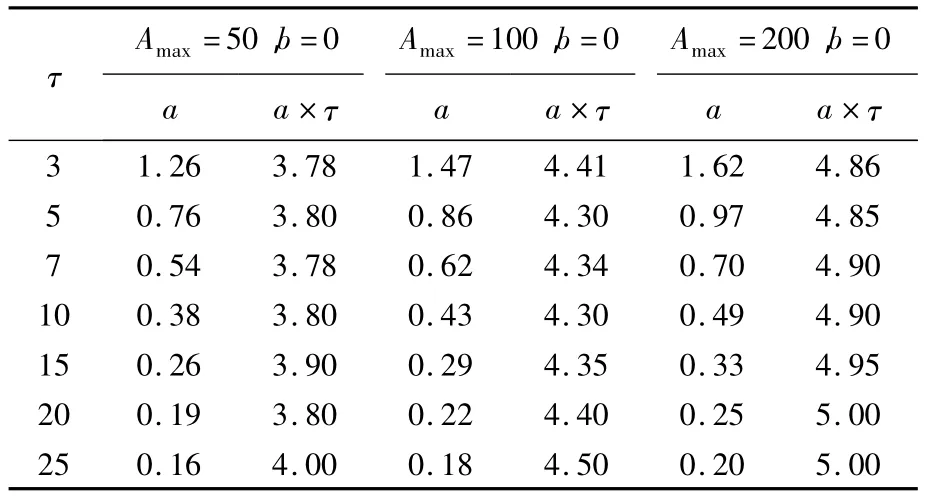
表1 ABDOM拟合ISPSDD结果

对理想软件缺陷发现时序过程的ABDOM拟合结果中发现，a的数值分布没有明显的规律，但是a×τ随Amax的增大，却是一个约略保持在4～5之间的数值，而b保持恒定数值0.

由于a≤0时，软件缺陷发现时序过程处在一个无法收敛的状态，因此可以设a=0时为临界点，即a×τ=0为软件缺陷发现时序过程不衰减的情况，在工程实践中这种状态揭示测试过程质量完全失去了控制.

依据理想测试质量状态下的a×τ的取值落在区间［0，4］或［0，5］这个发现，这里大胆推测在Amax=200条件下，a×τ的典型取值可以为5，4，3，2，1和0，分别代表测试开发过程的不同质量状态，即理想、优、良、中、差和失去控制，这暗中吻合软件过程CMM5级过程评级标准.

将推测得来的典型数据代入ABDOM模型进行观察，可以对软件缺陷发现时序过程曲线进行验证.在 Amax=100条件下，通过令 a×τ=4.5，3.5，2.5，1.5 和0.5 等不同取值，并令 τ=10，b=0，代入ADBOM模型，得到相应的软件缺陷发现时序过程曲线如图2所示.

从图2可以看出，当a×τ=4.5时，软件缺陷发现时序曲线的收敛状态接近于理想状态;当a×τ=3.5时，软件缺陷发现时序曲线的收敛状态优异;当a×τ=2.5时，软件缺陷发现时序曲线在第一波峰结束后有小波峰，收敛状态良好;当a×τ=1.5时，软件缺陷发现时序曲线在第一波峰后有多个快速收敛的波峰，收敛状态中等;当a×τ=0.5时，软件缺陷发现时序曲线剧烈振荡，收敛状态差.

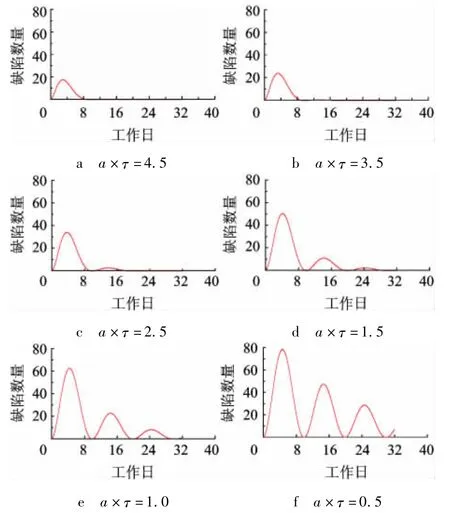
图2 不同a×τ取值下软件缺陷发现时序过程曲线范型(Amax=100，τ =10，b=0)

依据文献［1］的软件缺陷发现时序过程的双阻尼叠加振荡模型中测试项目实际数据拟合结果来看，以公文系统A为例，其 Amax=99，a=0.45，τ=3，a×τ=1.35，软件缺陷发现时序曲线的确处在中等收敛状态.以政务系统B为例，其Amax=28，a=0.07，τ=3，a × τ =0.21，软件缺陷发现时序曲线的确处在差的状态.这基本吻合了对a×τ的典型取值的推测.

2.3 软件缺陷发现过程质量指数

基于第2.2节，将ABDOM中的参数a进行改造，令Q=aτ，则有ABDOM-Q模型如下:

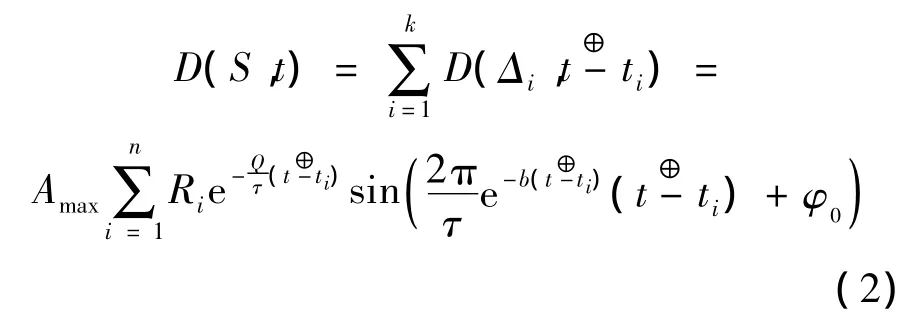
定义2 软件缺陷发现时序过程质量指数Q.该指数为ABDOM-Q模型中一个可规范化揭示软件缺陷发现时序过程质量的参数.Q的取值范围为(－∞，5］.

Q的典型取值与意义定义如下:

当Q在4～5之间时，过程质量接近于理想状态;

当Q接近于3.5，过程质量为优;

当Q接近于2.5，过程质量为良;

当Q接近于1.5，过程质量为中;

当Q接近于0.5，过程质量为差;

当Q接近0或小于0，过程质量为失控.

基于ABDOM-Q模型可以对软件测试过程中采集的软件缺陷发现时序数据进行拟合，拟合结果中Q的数值将可以辅助评估软件缺陷发现时序过程的质量.

2.4 基于ISPSDD的ABDOM的参数b研究

ABDOM模型中的参数b设计用来描述软件缺陷发现周期的衰减幅度.从物理意义上，当b=0时，表明软件缺陷发现周期保持恒定;当b＞0时，表示新的软件缺陷发现峰值来临的不断推迟或消失;而b＜0时，表示新的软件缺陷发现峰值来临的不断提前或与上一峰值合并.

这里参数b的取值范围定义为b∈(－∞，∞)，正常的测试过程中，b≥0，意味着有软件缺陷越来越难被发现的趋势，而b＜0则意味着可能有越来越多的软件问题有待发现，这在软件测试过程中属于要被关注的现象.

3ABDOM的离散化改进

在实际软件测试过程中，影响软件缺陷发现过程的因素很多，如开发组织与测试组织的变化、被测软件系统的变更、测试周期的延长或缩短.这种变化都是非连续的，这些因素导致原有ABDOM-Q模型中的固定不变或连续取值的Amax，Q，τ和b无法描述这种离散变化.为此本文中引入ABDOM-Q 模型离散化参数 Amaxi，Qi，τi和 bi，改进ABDOM-Q模型对软件缺陷发现时序过程各测试周期内参数离散变化的适应性.

在软件测试实践过程中，增量式测试是常见的一种测试演化类型.初次测试版本可能是已实现近乎全部需求的软件版本，后续只有部分小规模增量开发;也有可能是部分主干核心模块，后续有与初测模块规模相同或超出的软件模块加入.因此Ri的取值范围0＜Ri≤1可重新定义为Ri∈，以描述这种不断增加被测模块之间的比例关系和总和.改进后的ABDOM-Q具备描述离散化参数能力，称为ABDOM-Qd.ABDOM-Qd的数学描述如下:

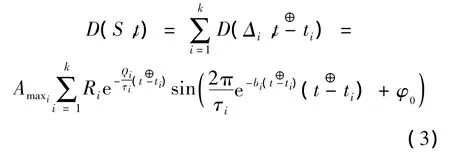
其中，i=1，2，3，…，k;t∈ Z+;Amax∈ Z+;τi∈Z+;Qi∈ (－ ∞，5］;bi∈(－ ∞，∞);Ri∈(0，1］

4 对ABDOM-Qd的检验

本节中，对ABDOM-Qd模型的检验基于某软件测试项目的缺陷发现时序数据开展.该项目是一个增量式测试，带有典型的离散特征.软件缺陷发现情况见表2.

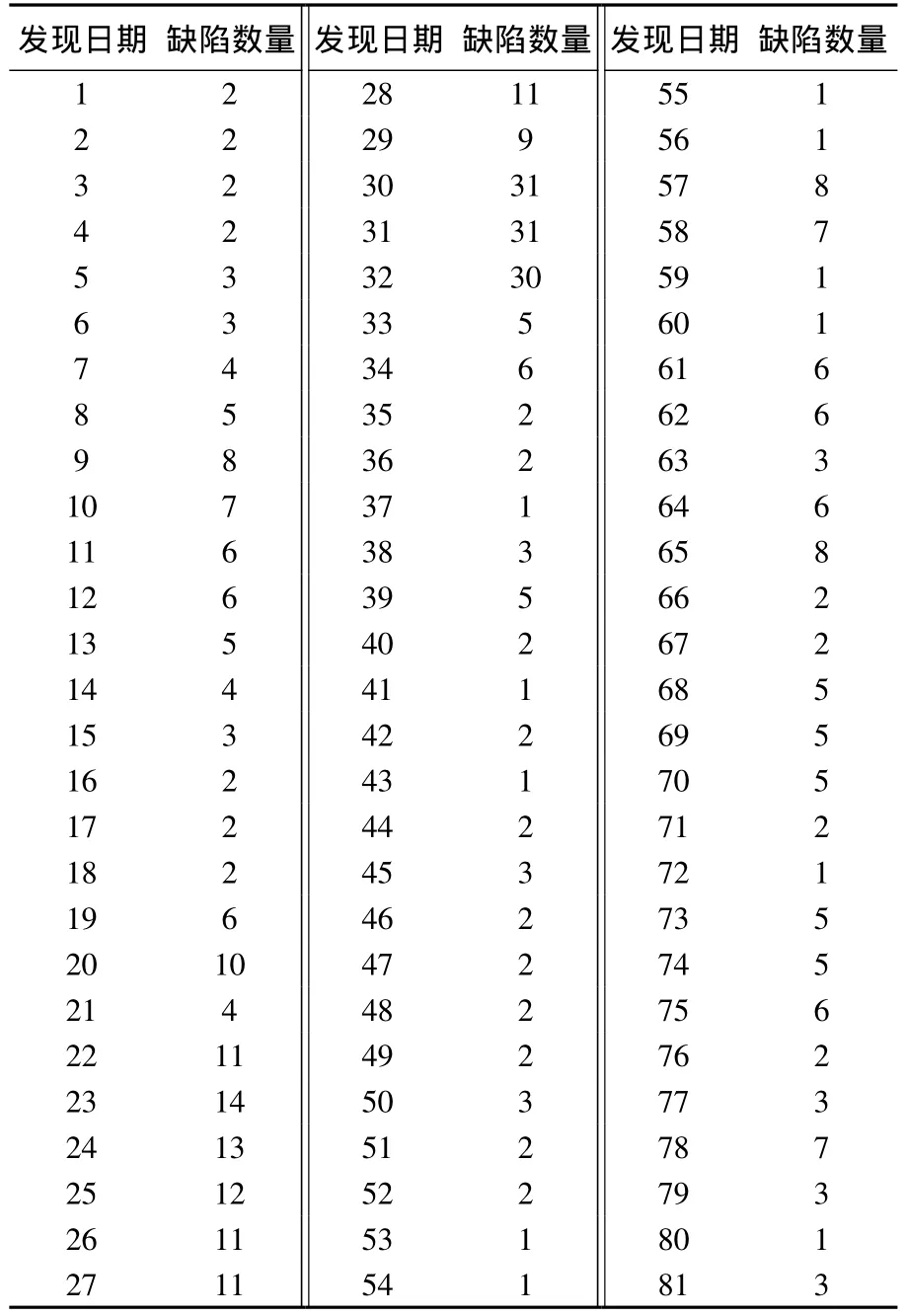
表2 某系统软件缺陷按时序发现统计

使用ABDOM-Qd对表2数据的拟合采用均方差最小值拟合法，获得了较好的拟合结果，如图3所示.

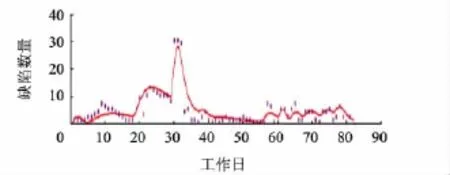
图3 ABDOM-Qd对某系统缺陷发现数据拟合曲线

最佳拟合结果选取的各参数取值范围如表3所示.式(3)与该项目实测数据的拟合效果较好，最小均方差为2.778821.

拟合结果表明，该测试项目属于多次增量式测试过程，有多达12个缺陷发现峰值;1;测试周期接近5的整倍，推测与每周5日工作有关;b=0.093;在正常范围内，Q的取值在0.5～0.8之间，揭示该测试项目的软件缺陷发现过程质量总体属于中等偏差水平.

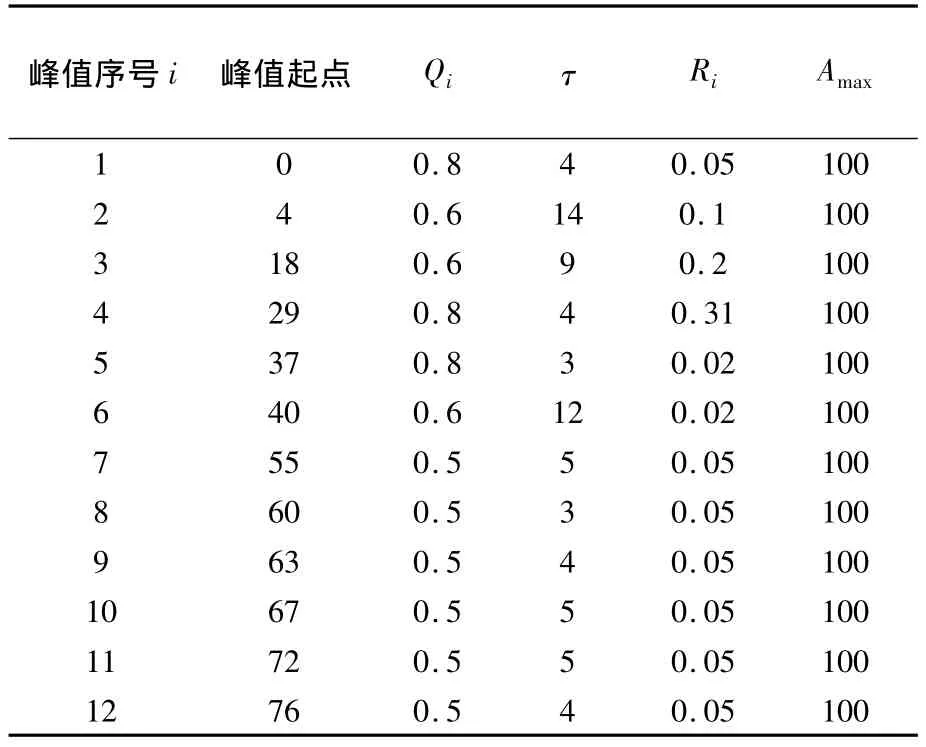
表3 ABDOM-Qd对某系统缺陷数据拟合结果

5 结论

经过对ABODM的参数规范化和离散化改进研究，有如下结论:

1)相比原有模型，ABDOM-Qd已具备描述复杂增量式开发、测试周期离散化、测试团队离散变化和测试过程质量离散变化等现实特征的能力;

2)提出了理想软件缺陷发现时序过程ISPSDD，并在此基础上提出了软件缺陷发现过程质量指数Q，该指数为定性评价一个软件测试过程的质量提供了直观依据，并进而可辅助评估软件测试的质量.

References)

［1］何智涛，晏海华，刘超.软件缺陷发现时序过程的叠加双阻尼振荡模型［J］.软件学报，2010，21(12):2999 －3010 He Zhitao，Yan Haihua，Liu Chao.Accumulative bi-damped oscillation model for the sequential process of software defect discovery［J］.Journal of Sofware，2010，21(12):2999 － 3010(in Chinese)

［2］王青，伍书剑，李明树，软件缺陷预测技术［J］.软件学报，2008，19(7):1565 －1580 Wang Qing，Wu Shujian，Li Mingshu.Software defect prediction［J］.Journal of Sofware，2008，19(7):1565 － 1580(in Chinese)

［3］Trachtenberg M.Discovering how to ensure software reliability［J］.RCA Engineer，1982，27(1):53 －57

［4］Jelinski Z，Moranda P.Software reliability research［C］//Freiberger W.Statistical Computer Performance Evaluation.New York:Academic Press，1972:465 －484

［5］Yamada S，Ohba M，Osaki S.S-shaped reliability growth modeling for software error detection［J］.IEEE Trans on Relibility，1983，R-32(5):475 －478

［6］王彤，王良，基于时序模型的Bug数的分析与预测［J］.现代计算机，2007，273(12):33 －36 Wang Tong，Wang Liang.Analysis and forecas ting of bugs based on time series model［J］.Modern Computer，2007，273(12):33－36(in Chinese)