考虑弹性影响的乘波体飞行动力学特性

向锦武 曾开春 聂 璐

(北京航空航天大学 航空科学与工程学院，北京100191)

乘波体构型近空间高超声速飞行器(乘波体飞行器)可用于天地往返运输系统和高速导弹，在军事和民用领域都具有广阔的应用前景.与常规飞行器相比，乘波体飞行器采用机体/发动机一体化设计，造成气动/推进的强烈耦合［1］.同时，由于其细长体外形的机体结构中使用了大量轻质材料，机体结构柔性大、振动频率低，在气动载荷激励下，可能发生显著的弹性变形和弹性振动.机体结构的大幅度弹性变形不仅改变了全机的气动特性，还引起推进系统空气流量以及入流参数的变化，形成乘波体飞行器特有的气动/弹性/推进耦合现象［2－3］.而机体的低频弹性振动则可能激发刚体动力学短周期模态，形成刚柔耦合现象.因此，结构弹性加剧了乘波体飞行动力学的耦合性，并使其呈现出多尺度、强非线性的特点，进而对总体设计和控制系统设计提出了严峻挑战.由于结构弹性参数会因设计更改而改变，并受到气动加热等因素的影响，其值可能在较大范围变化.因此，有必要研究结构弹性参数对乘波体飞行器多耦合飞行动力学特性的影响规律.

乘波体飞行器动力学特性分析的关键是建立多耦合动力学模型.目前，主要的建模方法包括基于FEM(Finite Elenent Melthod)结构模态计算的动力学建模［4］、基于 CFD(Computationd Fluid Dynamics)数值拟合的动力学建模［5］、基于近似理论方法的耦合动力学建模等［6－7］.前2种方法主要面向工程，其分析过程需要详细的结构布置与外形尺寸参数，而近似理论建模方法主要面向科学研究，其计算效率相对较高，是目前乘波体飞行器飞行动力学研究的主要建模方法.因此，本文采用近似理论建模方法，将气动外形、推进系统、结构模型等进行了简化处理，再分别利用近似理论气动力估算方法、瑞利流理论、假设模态法等建立了考虑多种耦合因素的动力学模型.研究了在不同机体结构刚度下，结构弹性对飞行动力学静配平特性及动态特性的影响规律，为总体设计及飞行控制系统设计提供了参考.

1 高超声速飞行器飞行动力学模型

典型的乘波体飞行器采用机体/发动机一体化设计.机体前部呈尖楔形，高超声速飞行时，产生附体斜激波，为飞行器提供升力，同时为发动机提供高压空气;机体后部是发动机的外喷管，产生额外的推力，同时也产生附加的升力和俯仰力矩.因此，动力学建模需要反映气动与推进的这种耦合关系.本文分别采用激波膨胀波方法、瑞利流理论、假设模态法等对气动、推进系统和结构弹性动力学进行建模，给出了考虑气动/推进/结构耦合的乘波体飞行器动力学模型.

1.1 气动力模型

采用基于激波膨胀波方法［7］的当地流活塞理论［8］给出高超声速非定常气动参数，进而建立了乘波体飞行器的气动模型.激波膨胀波方法适用于附体激波流动，能给出激波位置，适用的马赫数范围大，是计算高超声速附体激波流动气动力的基本方法.而牛顿冲击流理论［6］形式简单，可用于快速估算操纵面的气动力，一般适用于马赫数5以上.当地流活塞理论能够考虑非定常效应，其应用范围为马赫数1.2～10，但由于高超声速流动时的非定常效应影响较小，其使用限制可适当放宽.当地流活塞理论如式(1)、式(2)所示.

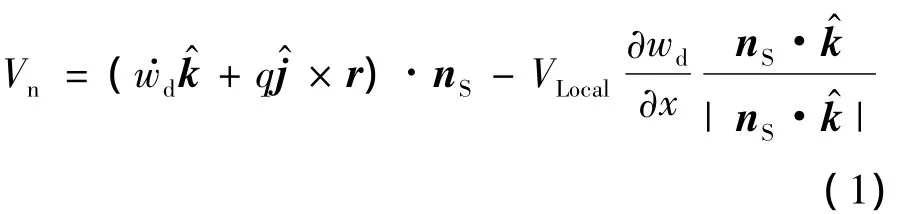
其中，Vn为气动微元瞬时法向扰动速度;q为俯仰角速度;∂wd/∂x 和分别为弹性变形转角和速度;aSE，pSE，VLocal分别为激波膨胀波方法计算的当地音速、压强和气流速度模量;利用当地流活塞理论修正的压强分布，可以积分得到各个气动面的气动力和力矩.此外，由于考虑了弹性变形的影响，以上建立的气动力模型能够反映气动与结构弹性的耦合.

1.2 推进系统模型

根据文献［6］的超燃冲压发动机模型，可以将发动机分成扩散段、燃烧室和内喷管.在激波膨胀波方法给出上游流动参数和激波位置的基础上，可以计算出推进系统的入流参数.再利用瑞利增能流［9］理论可以给出内流参数，具体计算方法参看文献［6］.在分析内流的基础上，根据发动机入流和出口参数，可给出推力的公式如下:

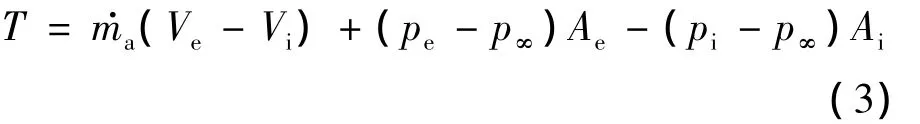
其中，下标i表示入口流动参数;下标e表示出口参数;下标∞表示自由流参数;为发动机气体流量.可以发现，发动机的状态强烈依赖于入流参数，而入流参数又决定于上游机体前部下表面的流动参数与激波位置，因此该建模方法能够考虑气动与推进的耦合.

1.3 机体结构弹性模型

乘波体飞行器刚度分布中部最大，并向两端递减，因此，弹性变形主要集中在两端.在缺乏数据的设计初期，这种弹性变形方式适合采用基于弹性集中假设的两段模型［6］.该模型在机身前部和后部连接的中部引入弹性铰，并假设变形时，前部和后部均刚性转动，弹性铰发生变形.此时，机体弹性变形位移wd可表示为模态广义坐标与模态函数的乘积:

其中，由于仅考虑一阶模态，因此i=1.根据拉格朗日方程可以得出质量归一化的弹性模态函数为

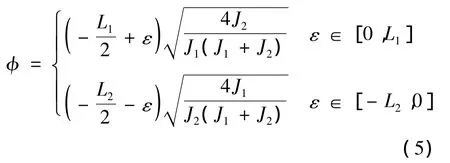
其中，J1，J2分别为重心前后机身段的俯仰转动惯量;L1，L2分别为飞行器前后机身段的长度.在模态坐标下，引入弹性模态广义力来计算结构弹性变形，其表达式为

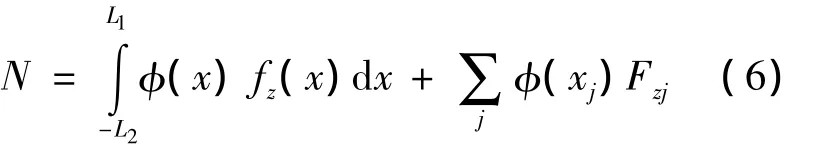
其中，fz为机体法向分布载荷;Fzj为法向集中载荷.机体前后部分中线的等效倾角改变量Δ1，Δ2与模态广义坐标的关系为

高超声速飞行器巡航飞行时，气动加热对结构力学特性影响较大，但相对于气动弹性响应，这种影响是一个缓慢的过程，因此本文将气动加热的影响考虑成结构刚度在一定范围内变化.

2 纵向飞行力学特性分析方法

从基本的拉格朗日方程出发，推导了纵向刚柔耦合的飞行动力学模型.机体坐标系下，柔性飞行器纵向运动学和耦合动力学方程如下:

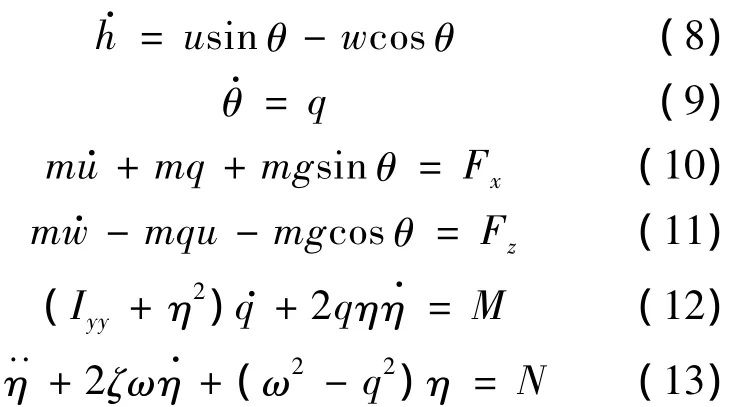
其中，状态变量h为高度;u为x向飞行速度;w为z向速度;θ为俯仰角;q为俯仰角速度;η为弹性模态广义坐标为弹性模态广义速度;下文分析中使用的迎角α可以近似由w与u的比值给出;Fx，Fz分别为x向和z向合力;M为俯仰合力矩;N为弹性广义力.

2.1 静态配平与飞行包线

求解静配平问题时，需要首先对方程式(8)～式(13)进行处理，即令飞行速度分量的时间导数和、俯仰角速度 q及其对时间的导数、弹性变形速度均为0，将原来的6个方程化简为5个.然后在指定飞行高度和速度，利用Newton-Raphson方法求解关于迎角α、俯仰角θ、升降舵偏转角δe(向下偏转为正)、发动机油门δT以及弹性广义坐标η等5个变量的非线性方程组，可获得静平衡解.

对于飞行包线，考虑以下3种边界条件:

1)最大动压边界:热防护系统的耐受范围决定了飞行的最大动压，其准确值需要由试验才能给出，本文取为95.76 kPa(2000 lb/ft).

2)发动机热阻塞边界:当发动机燃烧室出口马赫数低于1时，发动机会因热阻塞而不能正常工作.该边界是由可压缩流体力学理论［9］推导得出的，本文给出一定的裕度，即要求发动机燃烧室出口马赫数不得低于1.3.

3)最大油门边界:由于进入发动机的空气有限，因此当其中的氧气完全与燃油发生化学反应，即等效油门为1后，不能通过增大油门来增加推力.同时考虑到进入发动机的氧气并不能都发生化学反应，因此等效油门最大值取为0.9.

上述的3个边界条件中，条件1)确定了可配平飞行的最大速度和最低高度，其与飞行器参数无关，仅取决于大气环境和飞行速度;条件2)和条件3)确定了最低飞行速度和最大高度，二者均与飞行器的参数相关.本文在求解条件2)和条件3)时，首先选取了用于分析求解的马赫数值;然后分别针对每个马赫数值，使用二分法求解最大可配平高度;最后在速度-高度图中，将各个离散的边界点连接起来形成飞行包线.

2.2 动态特性

在配平状态下对方程式(8)～式(13)做线性化处理，可以得到如式(14)、式(15)所示的线性动力学分析模型.

3 机体刚度对飞行力学特性的影响

根据文献［7］给出的典型乘波体飞行器参数，从飞行动力学静配平特性、飞行包线要求、动态特性3个角度研究了机体结构刚度对飞行动力学特性的影响规律.

3.1 机体结构刚度对静态特性的影响

机体一阶弯曲自然频率ω1代表了机体弯曲刚度的大小，其值越大表明机体弯曲刚度越大.以下分析了配平参数随ω1的变化关系，其中ω1为圆频率，单位为rad/s.

图1 前体弹性变形等效倾角随马赫数的变化关系

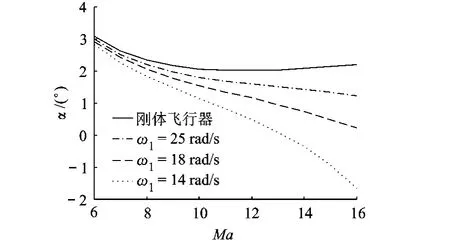
图2 迎角配平值随马赫数的变化关系

图3 配平状态下的全机升阻比随马赫数的变化关系

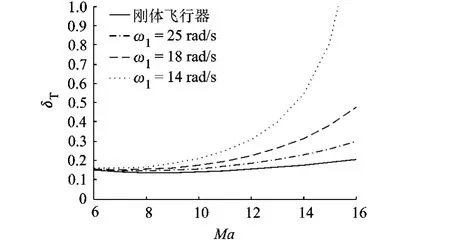
图4 油门配平值比随马赫数的变化关系

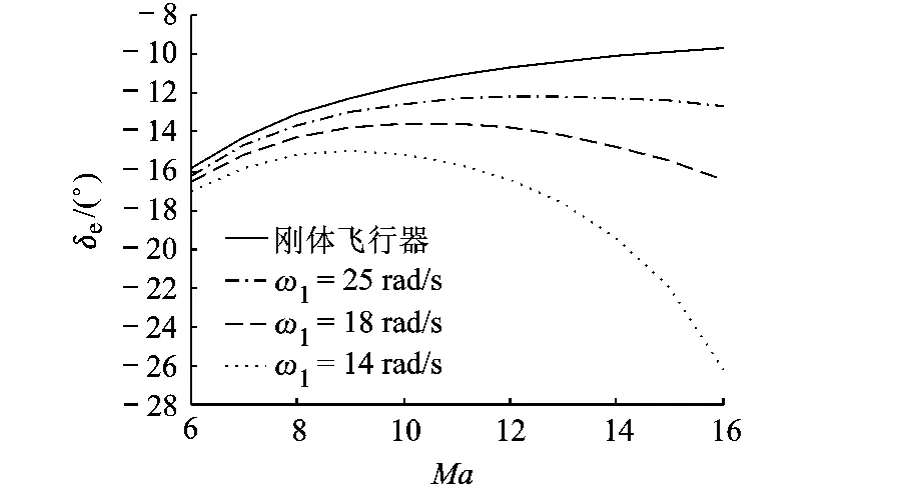
图5 升降舵配平值比随马赫数的变化关系

图1～图5为H=25 908 m(85 000 ft)，Ma=8，ω1分别为无穷大(刚体)，25，18，14 rad/s时，定常平飞状态参数和控制变量随马赫数的变化.可以看出:

1)在高马赫数下，结构弹性对飞行器的配平状态有较大的影响.对于同一机体刚度条件下的柔性飞行器，随着马赫数的增大，结构弹性变形引起的机体前部倾角急剧增大，甚至与设计角度接近，因而对静配平特性产生的影响不可忽略.

2)机体刚度下降会导致配平迎角减小.从图1、图2可以看出，在高马赫数段，随着结构刚度减小，结构变形引起机身前部下表面倾角增大，进而导致所需的配平迎角急剧减小.

3)机体刚度下降会导致飞行性能降低.从图3、图4可以看出，随着机体刚度下降，飞行器定常飞行时的升阻比将减小，所需的油门增大，并且在高马赫数段，该影响变得更加显著.

4)机体刚度下降会导致升降舵配平规律改变.从图5可以发现，在所有马赫数段，刚体飞行器的升降舵配平值随马赫数增大而减小，为正操纵;而对于ω1＜25 rad/s的柔性飞行器，在低马赫数区段，升降舵配平值随马赫数增大而增大，为正操纵;在高马赫数区段，升降舵配平值随马赫数增大而减小，变为反操纵.因此控制系统设计时，有必要检验柔性高超声速飞行器是否存在高马赫数区反操纵现象.

图6 是 ω1分别为∞，18，14，10rad/s时，乘波体飞行器的飞行包线.可以看出机体刚度减小会显著缩小高马赫数段的可配平区域.随着ω1的减小，发动机热阻塞边界向马赫数升高方向移动，而最大油门边界向高度减小方向移动，随着马赫数升高，其减小量增大.此外，还可以发现在 ω1=10 rad/s时，在马赫数16附近，最大油门边界存在不连续现象.分析其产生的机理首先要从高度对配平特性的影响入手，限于篇幅，本文直接给出结论:高度降低，刚体飞行器配平迎角减小，配平阻力减小，并且结构弹性变形增大.在该结论的基础上，可以发现，由于结构变形引起阻力增大，因此，当弹性变形引起的阻力增加与配平迎角减小引起的阻力减小相抵消时，通过降低高度的方式不能配平飞行器.

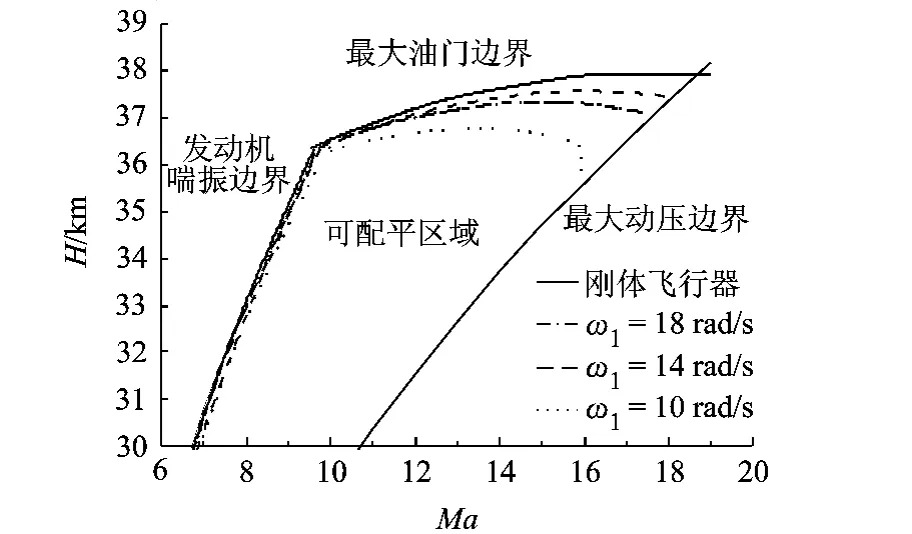
图6 不同机身弯曲刚度下的飞行包线

3.2 机体刚度对动态特性的影响

在H=25908 m，Ma=8状态下，分别计算ω1为∞，25，18，14 rad/s，升降舵为输入，轨迹角为输出的系统开环的零极点，如图7所示.可以看出，高超声速飞行器纵向飞行动力学存在3个模态，由5个特征根组成.其中短周期特征根由绝对值较大的一正实根和一负实根组成，表明其短周期缺少回复力，为静发散.随着机体弯曲刚度的减小，正实根进一步增大，加剧了短周期的不稳定.长周期模态由2个小阻尼、低频率共轭复根组成，随着机体弯曲刚度减小，其实部变化较小，而虚部向实轴靠近.高度模态对应一个绝对值接近0的实根，其随机体刚度变化较小.此外，还可以看出，机体弯曲刚度对零点位置的影响较小.综上所述，机体刚度降低，短周期模态稳定性急剧下降，进而使按照刚体模型设计的控制系统失效.

图7 开环零极点随机身刚度减小的变化

4 结论

通过对考虑机体弹性的乘波体飞行器的纵向飞行动力学建模、计算，分析了静态配平特性、飞行包线及动稳定性随机体弯曲刚度的变化规律，结果表明:

1)随着机体刚度减小，配平升阻比降低，耗油率增大，由发动机热阻塞和最大油门确定的飞行包线缩小;

2)当机体刚度较小时，飞行器升降舵配平规律在不同马赫数区段将发生变化，在低马赫数段升降舵操纵为正操纵，在高马赫数段变为反操纵;

3)纵向存在不稳定的短周期模态，机体刚度减小，长周期模态频率将降低，短周期模态正实特征根增大，从而使系统稳定性降低.

References)

［1］Fidan B，Mirmirani M，Ioannou P.Flight dynamics and control of air-breathing hypersonic vehicles:review and new Directions［R］.AIAA-2003-708，2003

［2］Cockrell C E，Engelund W C.Integrated aeropropulsive computational fluid dynamics methodology for the hyper-X flight experiment［J］.Journal of Spacecraft and Rockets，2001，38(6):836 －843

［3］黄喜元，王青，董朝阳.基于动态逆的高超声速飞行器鲁棒自适应控制［J］.北京航空航天大学学报，2011，37(5):560－563 Huang Xiyuan，Wang Qing，Dong Chaoyang.Robust adaptive control for hypersonic vehicle based on dynamic inversion［J］.Journal of Beijing University of Aeronautics and Astronautics，2011，37(5):560 －563(in Chinese)

［4］Heeg J，Zeiler T A，Pototzky AS，et al.Aerothermoelastic analysis of a NASP demonstrator model［R］.NASA-TM-109007，1993

［5］Clark A D，Mirmirani M D，Wu C，et al.An aero-propulsion integrated elastic model of a generic airbreathing hypersonic vehicle［R］.AIAA-2006-6560，2006

［6］Chavez F R，Schmidt D K.Analytical Aeropropulsive/Aeroelastic hypersonic vehicle model with dynamic analysis［J］.AIAA Journal of Guidance，Control，and Dynamics，1994，17(6):1308 －1319

［7］Bolender M A，Doman D B.Nonlinear longitudinal dynamical model of an air-Breathing hypersonic vehicle［J］.Journal of Spacecraft and Rockets，2007，44(2):374 －387

［8］McNamara J J，Crowell A R，Friedmann P R，et al.Approximate modeling of unsteady aerodynamics for hypersonic aeroelasticity［J］.Joural of Aircraft，2010，47(6):1932 －1945

［9］Anderson J D.Modern compressible flow［M］.2nd ed.New York:McGraw-Hill College，1995:77 －91

［10］方振平，陈万春，张曙光.航空飞行器飞行动力学［M］.北京:北京航空航天大学出版社，2005:219－220 Fang Zhenping，Chen Wanchun，Zhang Shuguang.Aircraft flight dynamics［M］.Beijing:Beihang University Press，2005:219 －220(in Chinese)