使用Gao－Yong湍流方程计算翼体角偶流动

高 歌 江立军 高 琳

(北京航空航天大学 能源与动力工程学院，北京100191)

翼体角偶流动在空气动力学和水动力学研究应用中广泛存在，例如，飞行器外流，叶轮机械，潜艇，电子元件冷却以及河流/桥梁流动等.它是一个强三维湍流边界层流动，有三维边界层的分离和再附;同时具有强三维各向异性，伴有多个马蹄涡的形成和发展，具有不同长度尺度的平板边界层和翼型边界层的相互干扰以及非定常特征等.正是因为这种湍流流动的复杂性，针对它的实验研究直到20世纪80年代才开始，详尽的实验数据直到90年代才由文献［1］给出.三维湍流流动的复杂性，使得以往湍流模式的评估与校正通常采用相对简单的二维边界层算例，这就导致将这些湍流模式应用于三维湍流流动时，给出的结果往往差强人意.文献［2］采用12种湍流模式，其中包括线性、非线性涡粘模式，雷诺应力湍流模式等，对翼体角偶流动进行了数值计算，得到的结果与实验对比相差甚远，其中雷诺应力模型表现最好，尤其是在尾迹区的马蹄涡结果捕捉较好，但没有一个模式得到与实验数据接近的结果，无论是平均流场还是湍流场.文献［3］用RANS/LES混合方法计算了翼体角偶流动，结果表明DES(Detached Eddy Simulation)预测分离过早，DDES(Delayed-Detached Eddy Simulation)结果稍有改善，但还是无法令人满意.Gao-Yong湍流方程［4］从Navier-Stokes方程出发，基于侧偏统计平均方法，在推导过程中不曾舍弃任何高阶湍流脉动量，模化过程中又采用了符合湍流物理实质的动量传输链概念，因而很好的保存了N-S方程的均化非线性特性.其独有的正交各向异性假设，使得该方程在强各向异性流动的数值模拟中表现优异.本文将Gao-Yong湍流方程添加进开源计算流体力学软件OpenFOAM中，并用于翼体角偶流动的计算，给出了令人满意的结果.OpenFOAM是一个用于计算流体力学和结构分析的C++类库，集中了CFD(Computational Fluid Dynamics)中可能用到的全部元素，比如网格类、场类、时间类、矩阵类、物理模型类等.正如文献［5］中介绍的，它采用操作符形式的方法描述偏微分方程的有限体积离散化，支持多面体网格，可以处理复杂的几何外形.经过十多年的发展，现在OpenFOAM已经成为开源CFD社区最受欢迎的开源CFD软件，是一个极好的研究和应用平台，正受到越来越广泛的关注［6］.由于C++的面向对象和模块化特性，使得OpenFOAM具有极强的扩展性和可维护性，本文的主要工作即是将Gao-Yong湍流方程加入其湍流模式模块中，并进行了相关的验证和数值计算工作.这一工作将极大地拓展Gao-Yong湍流方程工程应用的前景.

1 Gao-Yong湍流方程

侧偏平均思想初步形成于20世纪90年代，经过十几年的发展逐渐成熟:依据一定的原则将一点处湍流脉动划分为二组，每组的统计平均量均不为0，将各组的概率权重引入侧偏平均值之后获得了加权漂移速度的对称性，从而明确了各组侧偏平均量及其方程的对称性，为进一步引入加权漂移速度的正交各向异性奠定了基础.采用侧偏平均后获得了一阶统计平均量——漂移速度的独立动量方程和机械能方程，并利用唯象的动量传输链概念解决了封闭问题.二维GAO-YONG不可压湍流方程详见文献［4］，其最终完整的三维不可压湍流方程在文献［5］中直接给出:

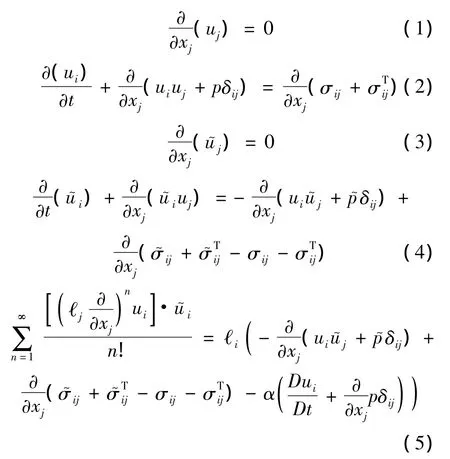
以上方程分别为平均流连续方程、动量方程、漂移流连续方程、动量方程以及机械能方程(漂移量有波浪上标).式中分别为平均流的层流应力和漂移流的层流应力，遵循广义牛顿定律所规定的应力和变形率关系分别为平均流湍流应力和漂移流湍流应力.详细的推导过程参见文献［7］，本文不再赘述.

2 计算模型与计算方法

本文研究对象是椭率为3∶2的椭圆头与NACA0020翼尾在最大厚度处结合的联合体和平板组成的角偶流动.此突体模型最大厚度为7.17 cm，弦长30.5 cm，高22.9 cm.自由来流平均速度27 m/s.流动雷诺数 Re0=U0T/ν=115 000，其中U0为自由来流平均速度，T为模型最大厚度，分别作为参考速度和参考长度.几何模型及采用的坐标系如图1所示.在计算中，取翼型前缘与平板相交处为坐标原点.x为流动方向，y沿展向，z垂直于平板方向.进口设在x/T=－11.2，进口边界条件、速度、湍流强度等均采用ERCOFTAC数据库的实验数据.出口设在x/T=14.0处，边界为沿流向零梯度.y方向的计算区域为y/T=－5到y/T=5，此两侧边界均采用可滑移条件.z方向的计算区域为z/T=0到z/T=3.2.上边界同样采用可滑移边界条件.此外，平板和翼型突体均为固体壁面，采用无滑移边界条件.

在x-y平面内用191×96的C型网格离散.在垂直平板的z方向，用56个网格离散.本文利用OpenFOAM现有求解器，采用空间离散的有限体积法、时间离散的隐式离散方法.因Gao-Yong湍流方程中的漂移流连续方程和动量方程形与平均流基本一致，故数值计算方法均采用SIMPLE算法，对流项离散格式采用二阶精度的TVD格式离散，扩散项采用中心格式离散.为避免使用非交错网格所引起的非物理压力波动，对有限体积界面上的速度采用了Rhie-Chow动量插值.离散的线性方程组采用预处理双共轭梯度法求解.

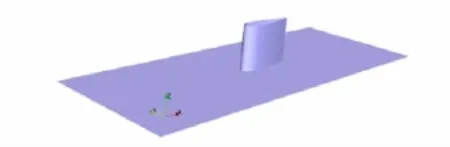
图1 计算几何模型

3 计算结果

实际上，翼体角偶流动是由两个边界层流动相互干涉而形成的一类复杂三维流动.其流动机理如下:平板远前方来流边界层受到因突体产生的逆压梯度影响，发生分离并绕自身卷起，涡团产生.当这个涡团随着主流逐渐接近突体时会拉伸变形，围绕突体形成所谓的马蹄涡.因为这种涡是由剪切层歪斜产生，根据普朗特的理论这可视为第1类二次流.许多研究者证实这个马蹄涡的强度和位置与突体前缘形状有关，一般说来，突体越钝，马蹄涡强度越大，位置越靠前.图2所示为使用Q准则描述的马蹄涡基本形状.图3给出了计算出的翼型头部对称面(x-z平面)内的流线分布，从图中可清晰地分辨出对称面内的回流旋涡，其中心大致位于(－0.21T，0.045T)，和实验测量结果(－0.2 T ，0.05 T)很接近.而且文献［1］中强调的在平板和翼型前缘相交处的极小区域内出现的二次分离涡，也被精确的捕捉到，见图3.

图4展示了平板和翼型表面的压力分布以及尾迹区的旋涡.结合以上两图可以得到翼体角偶流动的大体印象.从图4可以看到，由于计及Gao-Yong湍流方程中机械能方程的二阶项，尾迹区两侧旋涡相互干扰引起的非定常流动破坏了原本的对称性，使计算在一定程度上具备了模拟非定常流动的能力.

图2 使用Q准则得到的马蹄涡

图3 翼型前对称面流线图

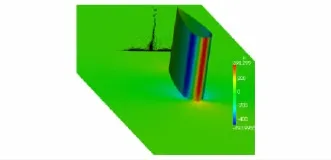
图4 壁面压力分布及尾迹区旋涡

本文采用的实验数据全部出自欧洲流体、湍流及燃烧研究协会对外公开的数据库(ERCOFTAC database:European Research Community ofn Flow，Turbulence and Combustion)，实验的相关情况在文献［1］中已做了详细介绍，本文不再赘述.图5和图6是不同高度处翼型表面的压力系数图，两者的位置分别为z/T=0.133和z/T=0.398.由这两图结合图4可以看出，翼型表面压力在最大厚度x/T=0.6以前，压力迅速减小.在这个位置之后，压力又渐缓升高.在翼型表面上，大部分区域是按这个一维规律变化的，但在最大厚度位置，受马蹄涡影响，沿垂直平板方向，越靠近平板，压力渐缓升高.如图5和图6所示，在翼型表面取两组数据与实验进行对比，两者定量符合得非常好.

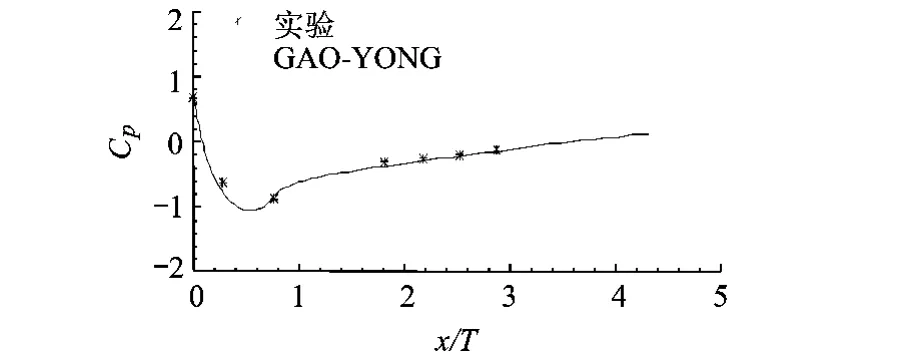
图5 z/T=0.133处翼型表面压力系数分布

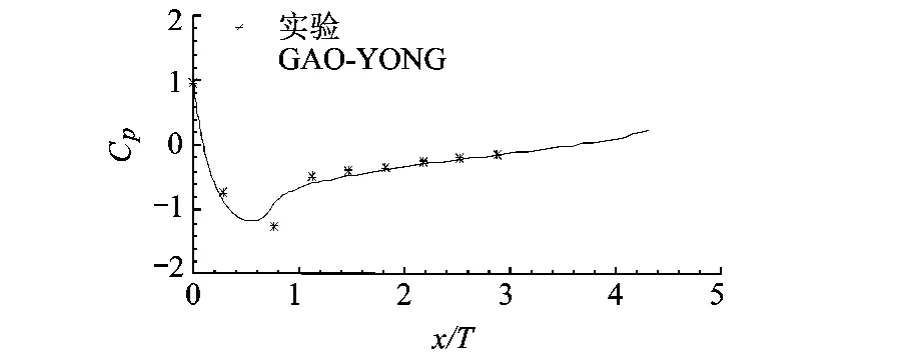
图6 z/T=0.398处翼型表面压力系数分布

图7和图8是翼型上游对称面上的速度型.图7为翼型上游不同位置沿流向速度U的分布，图8为z向速度W的分布.其坐标分别为x/T=－0.46，－ 0.4，－ 0.35，－ 0.3，－ 0.25，－ 0.2，－0.14，－0.1，－0.05.分离点上游和其附近的平均速度型与处于逆压梯度下二维边界层分离相似.当然，这种相似只是定性上的，边界层的增长被流体沿展向(y方向)的运动所限制.分离点下游不远处，平均回流只存在于临近壁面的狭长区域.计算结果和实验测量符合得非常好.从分离点位置，到回流旋涡的强度，都极好地重现了实验结果.在回流区，回流速度 U最大可达0.48Uref，计算结果基本重现了这一结论.法向速度W最大强度随着流动接近翼型突体逐渐增大，最高可达参考速度的30%，这个趋势也很好的捕捉到了.如图8所示，计算出的W速度型与实验数据基本重合，说明Gao-Yong湍流方程对这种复杂的三维流动能给出精确结果.图9是在x/T=0.76截面的y向速度分布.测量点坐标分别为:y/T=0.775，0.85，0.925，1.0，1.075，1.175，1.325，1.525.此处位于翼型最大厚度(x/T=0.6)的下游不远处，在靠近翼型突体附近是马蹄涡充分发展的区域，流动非常复杂.从图9可以看出，计算结果与实验测量结果基本符合.

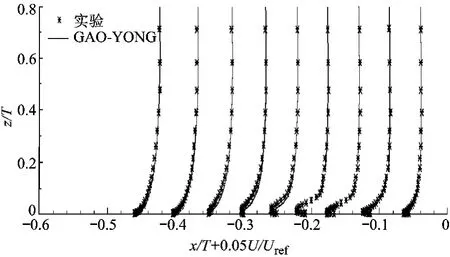
图7 翼型上游流向速度型

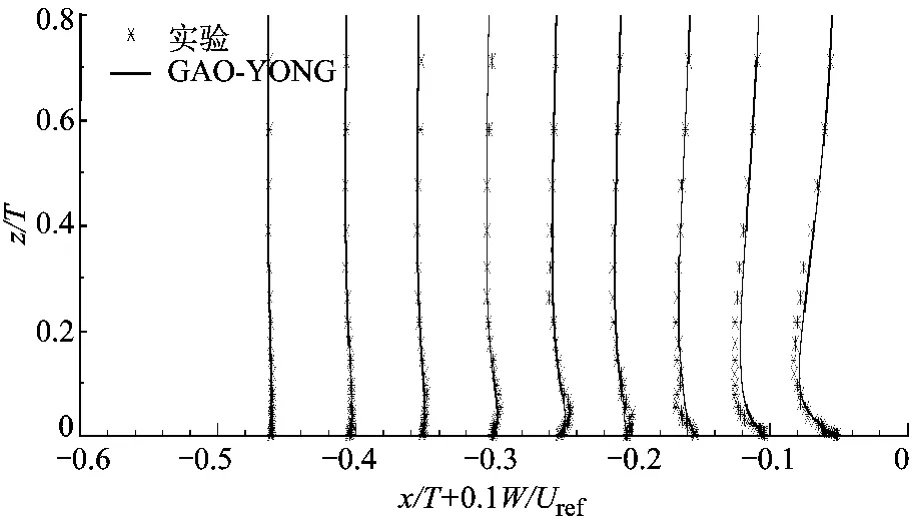
图8 翼型上游z向速度型

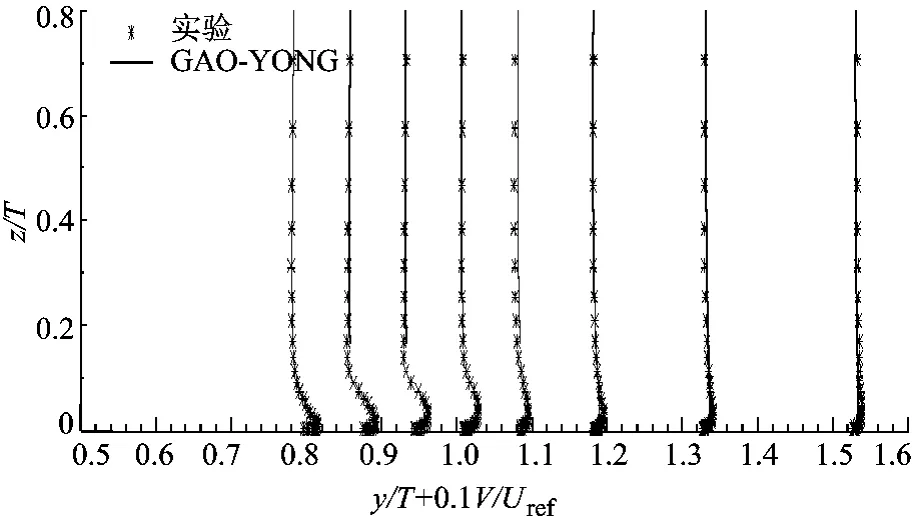
图9 x/T=0.76截面不同位置y向速度分布

4 结论

本文将三维不可压Gao-Yong湍流方程加入开源计算流体力学软件OpenFOAM中，并使用其对三维复杂边界层流动——翼体角偶流动进行了数值计算.计算完美捕捉到了此流动中的主要流动结构.无论是马蹄涡的位置，还是马蹄涡强度都得到精确结果.此外，对于固体壁面的压力分布，回流区及垂直流向截面的速度分布，数值计算都与实验结果符合得极好，证明Gao-Yong湍流方程有能力精确模拟翼体角偶流动这类复杂的三维边界层流动.由于整个计算基于OpenFOAM这个强大的开发平台，使得网格划分，结果分析等前后处理过程极为方便，这就将Gao-Yong湍流方程向工程实际应用方向推进了一大步.

References)

［1］Devenport W J，Simpson R L.Time-dependent and time-averaged turbulence structure near the nose of a wing-body junction ［J］.Journal of Fluid Mechanics，1990，210:23 －55

［2］Apsley D D，Leschziner M A.Investigation of advanced turbulence models for the flow in a generic wing-body junction ［J］.Flow，Turbulence and Combustion，2001，67:25 －55

［3］Fu Song，Xiao Zhixiang，Chen Haixin，et al.Simulation of wingbody junction flows with hybrid RANS/LES methods［J］.International Journal of Heat and Fluid Flow，2007，28:1379 －1390

［4］Gao Ge，Yong Yan.Partial-average-based equations of incompressible turbulent flow ［J］.International Journal of Non-Linear Mechanics，2004，39(9):1407 －1419

［5］Weller H，Tabor G，Jasak H，et al.A tensorial approach to computational continuum mechanics using object-oriented techniques［J］.Computers in Physics，1998，12(6):620 －631

［6］江立军，高歌，张常贤.三维斜掠后台阶数值模拟［J］.北航学报，2010，36(1):87 －90 Jiang Lijun，Gao Ge，Zhang Changxian.Numerical simulation of a swept backward-facing step flow［J］.Journal o f Beijing University of Aeronautics and Astronautics，2010，36(1):87 － 90(in Chinese)

［7］高歌，熊焰.侧偏平均湍流方程研究综述［J］.中国力学文摘，2008，22(2):1 －20 Gao Ge，Xong Yan.A review on the research development of Gao-Yong equations of turbulent flows［J］.Chinese Mechanics Abstracts，2008，22(2):1 － 20(in Chinese)