Bernstein多项式于一重积分Wiener空间下的平均误差

马海腾，解 静，许贵桥

（1.天津天狮学院 公共基础教学部，天津301700；2.天津师范大学 数学科学学院，天津300387）

1 引言及主要结果

设F是一个实可分的Banach空间，μ是定义在F的Borel子集上的概率测度.G是另一个范数为‖·‖ 的线性赋范空间，F连续嵌入到G.任意使得f→‖f－A（f）‖为可测映照的算子A：F→G被称为一个逼近算子.算子A的p－平均误差定义为

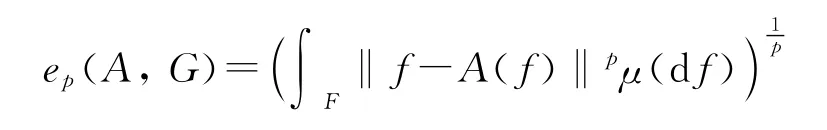
由于实际问题中的目标函数常常仅由函数在有限点的值给出，因此逼近算子A（f）常常仅由函数f在相应点的值给出.许多文章[1－4]都研究了这种算子在平均情形下的计算复杂性.考虑到Bernstein多项式是一类仅依赖于函数在有限点值的重要逼近工具，本研究考虑Bernstein多项式在一重积分Wiener测度下的平均误差.

设F是由定义在[0，1]上的连续函数赋予最大范数所构成的线性赋范空间，且f（0）＝0.Wiener测度ω由下列性质唯一确定：对任意n≥1，B∈B（Rn）（B（Rn）表示Rn上所有Lebesgue可测子集构成的集类）及0＝t0＜t1＜…＜tn≤1，

其中u0＝0.其关联算子为

设f∈C1[0，1]，则函数f的n次Bernstein多项式的导数为[5]

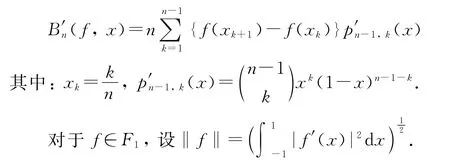
定理 设B′n（f，x）如上定义，则有

这里及以下的A（n）≈B（n）表示存在不依赖于n的正常数C，使得A（n）／C≤B（n）≤CA（n），且不同式中的C可以不同.

2 引理

引理1[6]对于任意的0≤x1≤x2≤x3≤x4≤1，有

引理2[5]若则对于所有满足不等式的k，渐近关系式

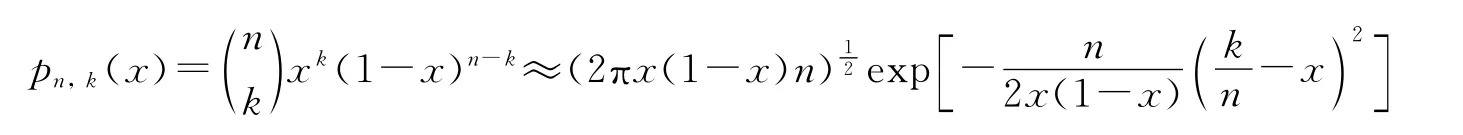
一致成立.

由式（2）容易计算得：

引理3 当xi≤xj时，有

3 定理的证明

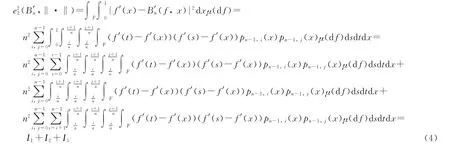
先考虑I2，

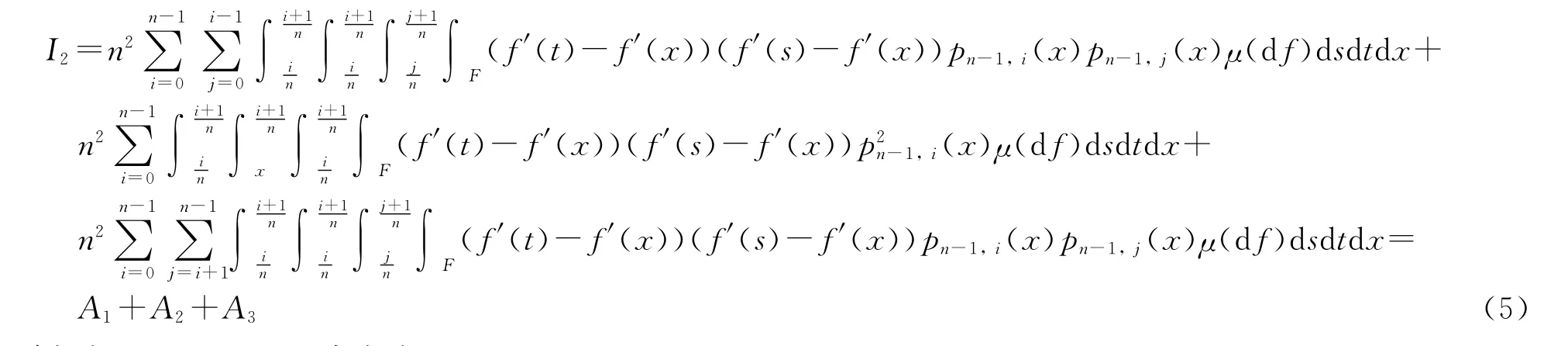
分别考虑A1、A2、A3.先考虑A2，

由式（6）～式（8）知

再考虑A3，由式（2）易知

类似可得

由式（5）、式（9）～式（11）可得

再考虑I1，

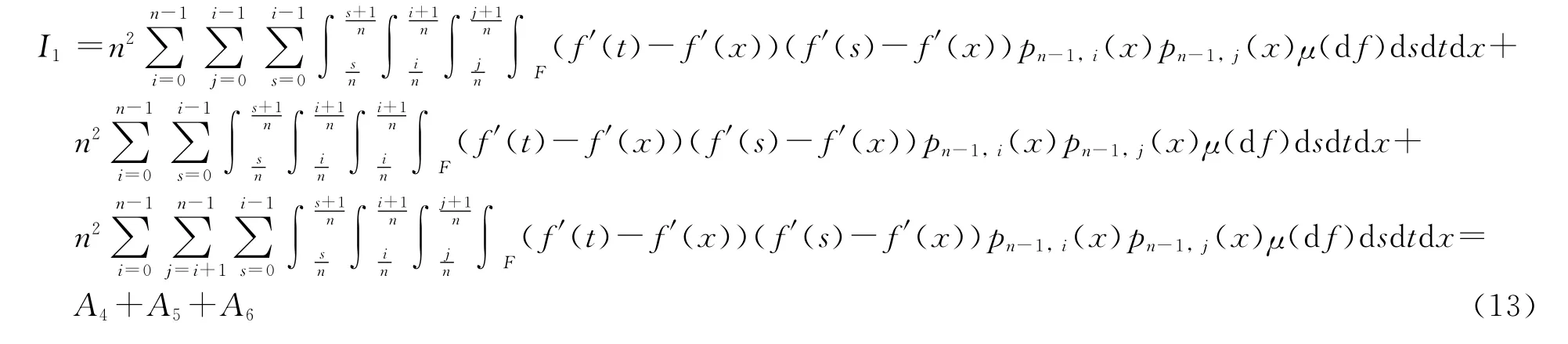
由式（13）～式（16）可得

类似可得

下面考虑下界，由文献[7]可得

易知

由式（19）～式（20）可得

由式（4）、式（12）、式（17）～式（18）、式（21）～式（22）可得定理结论.

[1]TRAUB J F，WASILKOWSKI G W，WOZNIAKOWSKI H.Information－Based Complexity[M].New York：Academic Press，1988.

[2]KLAUS R.Approximation and optimization on the Wiener space[J].J Complexity，1990，6：337－364.

[3]HICKERNELL F J，WOZNIAKOWSKI H.Integration and approximation in arbitrary dimensions[J].Adv Comput Math，2000，12：25－58.

[4]KON M，PLASKOT L.Information－based nonlinear approximation：An average case setting[J].J Complexity，2005，21：211－229.

[5]LORENTZ G G.Bernstein Polynomials[M].Toronto：Univ Toronto Press，1953.

[6]XU G Q.The average error for Lagrange interpolation and Hermite－Fejér interpolation on the Wiener space[J].Acta Mathematica，2007，50（6）：1281－1296.

[7]XU G Q，DU Y F.The average error for Hermite－Fejér interpolation on the Wiener space[J].Science in China：Series A，2008，51：1－3.

[8]RONALD A D，LORENTZ G G.Constructive Approximation[M].Berlin：Springer－Verlag，1993.