具时滞细胞神经网络周期解的全局渐近稳定性

常 青，周立群

（天津师范大学 数学科学学院，天津300387）

细胞神经网络模型自1988年由Chua等[1]首次提出以来，在理论与应用中已被广泛研究.细胞神经网络是一种能实时、高速并行处理信号的大规模非线性模拟电路模型，易于VLSI实现.因而细胞神经网络在图像处理、模式识别、联想记忆、通信保密及组合优化等领域都有着广泛的应用前景.细胞神经网络的动力学行为对网络的动态性质，如平衡点的存在性、唯一性，全局渐近稳定性或指数稳定性有着重要的影响，而平衡点的性质在细胞神经网络的应用中起着重要作用.平衡点可视为细胞神经网络的具任意周期的一个特殊的周期解，因而对细胞神经网络的周期解的研究也有重要意义.

在关于细胞神经网络周期解的稳定性的研究中，主要的方法有Lyapunov泛函[2－4]、重合度理论中的Mawhin延拓定理[5－7]、不动点定理[8]、Halanay不等式[9]等，或者是其中几种方法的结合.如文献[10]利用重合度理论中的连续性定理及Lyapunov泛函研究了具分布时滞细胞神经网络周期解的存在性和全局稳定性；文献[11]利用Lyapunov泛函及Halanay不等式研究了具时变时滞和分布时滞细胞神经网络周期解的全局指数稳定性；文献[12]利用重合度理论中的连续性定理及合适的退化Lyapunov－Krasvovskii泛函研究了具时滞和脉冲细胞神经网络周期解的存在性和全局指数稳定性；文献[13]利用Lyapunov泛函和Young不等式研究了具常时滞和变时滞模糊细胞神经网络的全局指数稳定性和周期解的存在性.在控制系统的稳定性分析中得到广泛应用的Barbalat引理，也可应用于非线性自治系统的渐近稳定性分析.因而本研究利用Barbalat引理及Lyapunov泛函讨论具时滞细胞神经网络周期解的全局渐近稳定性，得到了具时滞细胞神经网络周期解的全局渐近稳定性的新的充分条件.

1 模型与预备知识

考虑如下具时滞细胞神经网络的数学模型：

其中：t＞0；n是网络中神经元的个数；xi（t）表示第i个神经元在t时刻的状态变量；fj（xj（t））表示第j个神经元在t时刻的输出；di＞0表示在与神经网络不连通并且无外部附加电压差的情况下第i个神经元恢复独立静息状态的速率；aij、bij是常数，分别表示第j个神经元在t时刻的输出对第i个神经元的影响强度和第j个神经元在t－τj时刻的输出对第i个神经元的影响强度；τj是非负常数；Ii（t）是周期为ω＞0的输入函数.

系统（1）的初始条件为

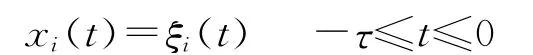
假设系统（1）的输出函数满足下列条件：

（C2）fi（x）满足全局Lipschitz连续，即存在li＞0，使得

定义 设φ（t）＝（φ1（t），φ2（t），…，φn（t））T是系统（1）的周期解，若系统（1）从任意初始函数ξ（t）＝（ξ1（t），ξ2（t），…，ξn（t））T出发的解轨迹x（t；ξ（t））都满足

则称系统（1）的周期解φ（t）是全局渐近稳定的.

引理1[14]（Barbalat引理） 如果函数φ（t）、（t）有界，而且φ（t）平方可积，则φ（t）＝0.

引理2 设fi（x）满足（C1），则系统（1）的解有界.

证明 ∀t＞0，系统（1）的解可表示为

因此，系统（1）的解有界.

2 主要结果

定理 假设（C1）、（C2）成立，如果则系统（1）的周期解是全局渐近稳定的.

证明 设φ（t）＝（φ1（t），φ2（t），…，φn（t））T是系统（1）的周期解，令yi（t）＝xi（t）－φi（t），则有

构造正定Lyapunov泛函

对V（y（t））沿系统（1）求导得

设t≥0，上式两边同时从0到t积分得

于是有

由引理2知系统（1）的解x（t）＝（x1（t），x2（t），…，xn（t））T在t≥0上有界，即xi（t）在t≥0上有界，由式（1）知在t≥0上也有界.而φ（t）是系统（1）的周期解，则在t≥0上也有界.又因为yi（t）平方可积，则由引理1知因此，系统（1）是全局渐近稳定的，即系统（1）的任意解都收敛到它的周期解.

在系统（1）中，若对任意i＝1，2，…，n，都有Ii（t）＝Ii，则系统（1）变为

由定理可直接得到如下推论：

推论 假设（C1）、（C2）成立，如果则系统（2）的平衡点是全局渐近稳定的.

3 数值算例

例1 考虑如下具时滞细胞神经网络：

其中：

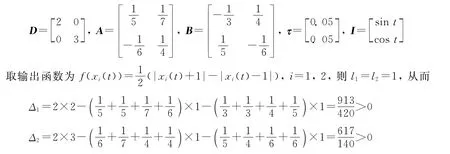
因此，由定理得系统（3）的任意解都收敛到其周期解.仿真结果见图1.

图1 系统（3）的仿真图Fig.1 Simulation figure of system （3）

例2 考虑如下具时滞细胞神经网络：

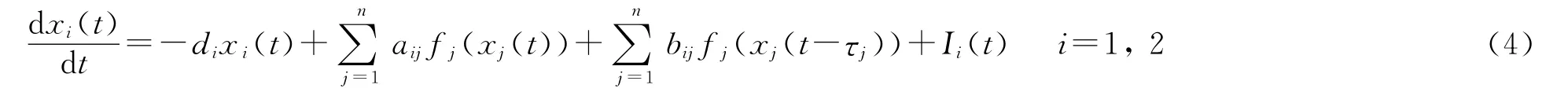
其中：

因此，由定理得系统（4）的任意解都收敛到其唯一周期解.仿真结果见图2.

图2 系统（4）的仿真图Fig.2 Simulation figure of system （4）

4 结论

讨论了一类具时滞细胞神经网络周期解的全局渐近稳定性，通过构造合适的Lyapunov泛函及应用Barbalat引理，得到了具时滞细胞神经网络周期解的全局渐近稳定性的新的充分条件，所得条件与时滞无关，更具一般性.

[1]CHUA L O，YANG L.Cellular neural networks：Theory and applications[J].IEEE Transactions on Circuits and Systems，1988，35（10）：1257－1290.

[2]CAO J D.On exponential stability and periodic solutions of CNNs with delays[J].Physics Letters A，2000，267（5／6）：312－318.

[3]DONG M F.Global exponential stability and periodic solution of CNNs with delays[J].Physics Letters A，2002，300（1）：49－57.

[4]FANG S L，JIANG M H，FU W F.Global exponential stability and periodicity of CNNs with time－varying discrete and distributed delays[J].Lecture Notes in Computer Science，2008，52：138－147.

[5]李必文，郑绿洲.具有两个神经元的时滞细胞神经网络的周期解[J].华中科技大学学报，2005，33（9）：117－127.

[6]李必文，万素梅.具变时滞细胞神经网络的周期解[J].数学杂志，2007，27（4）：483－488.

[7]龙辉平，王友琼.具变时滞细胞神经网络的周期解[J].数学理论与应用，2009，23（1）：103－105.

[8]ZHAO H Y.Global exponential stability and periodicity of cellular neural networks with variable delays[J].Physics Letters A，2005，336（4／5）：331－341.

[9]周立群，胡广大.具分布延时细胞神经网络的指数周期解与稳定性[J].系统仿真学报，2008，20（10）：2511－2514.

[10]LI Y K.Global stability and existence of periodic solutions of discrete delayed cellular neural networks[J].Physics Letters A，2004，333（1／2）：51－61.

[11]ZHOU L Q，HU G D.Global exponential periodicity and stability of cellular neural networks with variable and distributed delays[J].Applied Mathematics and Computation，2008，195（2）：402－411.

[12]WANG H，LI G D，XU H B.Existence and global exponential stability of periodic solution of cellular neural networks with delay and impulses[J].Results in Mathematics，2010，58（1／2）：191－204.

[13]ZHANG Q H，LUO W，YANG L H.Analysis of global exponential stability and periodic solutions of FCNNs with constant delays and time－varying delays[J].Journal of Applied Mathematics and Computing，2011，37（1／2）：459－471.

[14]贺昱曜，闫茂德.非线性控制理论及应用[M].西安：西安电子科技大学出版社，2007.