基于干扰消减的认知无线电频谱分配算法

杜文峰，刘亚涛，明仲，隋银雪

（深圳大学 计算机与软件学院，广东 深圳 518060）

1 引言

随着无线通信技术的快速发展，无线频谱资源变得十分稀缺，已经无法满足日益增长的无线通信技术需求。然而，根据美国FCC于2003年对无线频谱使用情况的调查报告[1]，可以发现已分配的授权频谱的资源利用率普遍在 15%～85%范围内波动。2009年，中国移动研究院无线技术研究所对授权频谱的利用情况进行了实测，结果表明已分配的授权频谱资源的利用率很低，多半频段的利用率不足5%，甚至出现空白频段[2]。因此，如何提高授权频段的重复利用率，缓解当前无线网络带宽资源紧缺的现状，成为当前无线通信领域亟待解决的问题。认知无线电 (CR, cognitive radio)正是在这样的环境下提出的一种频谱资源共享技术[3]。

认知无线电通过实时感知外部频谱的使用情况，发现并利用闲置的授权频段（称为“频谱空穴”）进行数据传输，实现频谱资源的动态共享。在认知无线电网络中存在着2类用户：主用户(PU, primary user)和认知用户(CU, cognitive user)。主用户是在指定频段上的法定授权用户；认知用户没有任何频谱使用授权，只是伺机占用主用户未使用的授权频段进行通信。

目前，已有部分研究针对认知无线电的频谱分配过程展开了讨论，通过分析多个相互竞争的认知用户之间的关系，将授权频谱分配给满足一定条件的认知用户使用。可以发现，现有的频谱分配算法在分配过程中主要以特定的目标函数为指导，并未考虑到频谱分配过程的公平性。此类算法在分配过程中以最大化目标性能为主导，可能将频谱资源优先分配给部分竞争力较强的认知用户，导致其他竞争力较弱的认知用户由于可用频谱被占用而无法接入。而此时，另外一些授权频谱资源由于没有认知用户接入而继续空置，产生“饿死”现象。

然而，在认知无线电网络环境中，由于不同认知用户的接入方式或发射功率不一定相同，处于同一授权频谱覆盖范围内的多个认知用户在接入和使用频谱的过程中可能出现干扰或者能够共享使用。同时，授权频谱分配的先后次序也将影响频谱分配的最终结果。本文正是在此基础上，针对认知用户在接入授权频谱的竞争过程中所产生的冲突进行分析，提出了一种基于干扰消减的频谱分配算法(IESA, interference elimination based spectrum allocation algorithm)。该算法通过消减认知用户在接入频谱过程中存在的干扰，增加能够同时接入授权频谱的认知用户数量。同时，本算法将各个认知用户的可用频谱信息结合到频谱分配过程中，对分配过程的公平性进行了优化。

本文的后续内容组织如下：第2节介绍了当前认知无线电频谱分配问题的研究现状；第3节使用图论方式对频谱分配过程进行建模；本文提出的频谱分配算法将在第4节给出；第5节对比了本算法与颜色敏感图着色算法的运行性能，并给出了模拟仿真结果；第6节是结束语。

2 相关研究

在认知无线电网络中，认知用户由于所处位置不同，可能被多个授权频谱所覆盖，能够感知和接入多个授权频谱。

目前，针对认知无线电频谱分配方面的文章主要以图着色理论模型为基础。文献[4]提出了基于列表着色的分布式贪婪算法，以最大频谱分配数量为目标，将认知用户同其他认知用户所产生干扰的数量定义为该认知用户的度，并优先对度较小的认知用户进行频谱分配。以认知用户之间的干扰度来进行频谱分配能够优化认知用户占用频谱的数量，但分配结果中有可能出现一个用户占用多个频谱的情况，导致其他多个认知用户无法接入。同时，该算法缺乏对干扰和频谱效益的差异性讨论；Haitao Zheng等在文献[5]中利用不同认知用户在使用频谱资源时所产生的效益和干扰差异性，提出了一种以最大效益为目标的颜色敏感图着色算法(CSGC,color sensitive graph coloring algorithm)。该算法将频谱效益与用户干扰度的比值定义为标号，并优先对标号最大的节点进行分配，提高系统的频谱效益。然而，在该算法中产生频谱效益较大的认知用户往往由于竞争优势抢占产生频谱效益较小的认知用户所能够使用的频谱资源，无法保证认知用户的最大频谱接入数量；文献[6]中设计了一种启发式规则来进行频谱分配和频谱资源调度，实现了以网络公平性为目标的频谱共享。Anh Tuan Hoang等在文献[7]中采用功率控制方法来计算不同认知用户的信噪比，通过降低认知用户对授权用户的干扰，对频谱使用过程进行优化。然而，该算法主要针对认知用户接入授权频谱的干扰问题进行讨论，没有对多个认知用户同时接入相同授权频谱时所存在的同频干扰问题进行分析；文献[8]以认知用户的接入公平性为参考，提出了一种基于流量感知的认知无线电网络动态频谱分配算法。该算法通过感知不同节点的网络流量，有选择地为认知用户进行频谱分配，在一定程度上提高了认知用户使用频谱资源的公平性；文献[9]通过建模认知用户和主用户的行为模式，对认知用户阻塞主用户，以及同主用户产生接入冲突的概率进行预测。通过将不同认知用户分配到不同的授权频段，能够在一定程度上提高网络的吞吐量，同时保证频谱分配的公平性。

可以发现，目前已有的频谱分配算法主要以系统最大频谱效益为目标，优先将可用频谱分配给产生较大频谱效益的认知用户。尽管该类算法能够有效地解决接入冲突问题，但仍缺少对多个认知用户共享同一频谱问题的讨论。同时，现有部分频谱分配算法优先对满足一定目标的认知用户进行频谱分配，可能导致其他认知用户由于可用频谱被占用，而另外一些可用授权频谱资源由于没有被接入而继续空置的情况，限制了接入到可用授权频谱中的认知用户数量。

另外，已有的频谱分配算法主要强调认知用户之间的同频干扰，不允许多个认知用户共享接入同一个授权频谱。然而，由于认知用户的接入方式或发射功率不一定相同，处于同一授权频谱覆盖范围内的多个认知用户在接入和使用频谱的过程中由于互不干扰，可能共享使用该频谱。本文以认知节点的发射功率，即信号传输距离为例来定义不同认知用户之间的同频干扰。当认知用户之间的距离低于一定阈值时，同一频谱覆盖范围内的认知用户将由于接入干扰而不能共享该频谱资源；反之，当认知用户之间的距离超过某一阈值时，认知用户的频谱接入过程将不存在干扰，可以共享该授权频谱进行通信，如图1所示。认知节点1和认知节点2可以同时接入授权频段A，而认知节点3与认知节点1和认知节点2在接入频谱过程中将产生同频干扰。

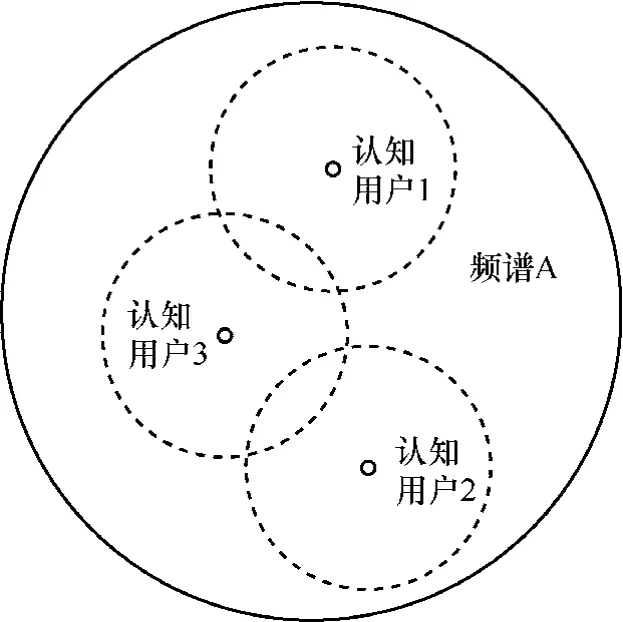
图1 认知无线电网络频谱覆盖及接入

为了进一步优化认知无线电网络的频谱分配过程，使得多个互不干扰的认知用户能够共享同一授权频段，并且保证频谱分配过程中的公平性，本文在已有认知无线电干扰消除问题分析的基础上，进一步针对同频干扰消除问题进行优化，通过对能够共享同一授权频谱的多个认知用户情况进行分析，结合频谱干扰和频谱效益的差异性，在增加认知用户接入数量的同时提高系统的频谱利用率。

3 系统模型与假设

假设认知无线电网络中的授权频谱可以划分为M个互不干扰的正交频段，即信道，且每个信道的传输频率和覆盖范围各不相同。其中，信道j用SRj表示，1≤j≤M。认知无线电网络中存在着N个认知节点，每个认知节点代表一个认知用户。其中，第i个认知节点用CRi表示，1≤i≤N；认知用户由于所处位置不同，则可能处于多个授权频谱的覆盖范围内。认知用户可以接入到其可感知的任何一个可用授权频谱进行通信。认知用户之间由于接入技术或传输距离等原因，在接入同一信道时可能会产生频谱干扰。

同时，本文假设在频谱分配过程中，认知无线电网络环境不发生改变，即认知用户的位置、可用授权频段不发生变化。

为了描述认知无线电网络的频谱分配过程，本文同样利用图着色理论来描述整个认知无线电网络场景。类似文献[5]，本文引入了可用矩阵、效益矩阵、干扰矩阵和分配矩阵。同时，本文对干扰矩阵进行了扩展，使其能够更好地描述现实环境。

1) 可用矩阵L={li,j|li,j∈{0, 1}}N×M, 1≤i≤N,1≤j≤M，是关于认知用户和授权频谱资源可用关系的二维矩阵。其中，行标i表示认知用户 CRi，列标j表示授权频段SRj。如果认知用户CRi可以接入授权频谱SRj，则记li,j=1；否则，记li,j= 0。

2) 效益矩阵B与可用矩阵L对应，以bi,j表示认知用户CRi接入频谱资源SRj时所产生的频谱效益。若CRi无法接入频谱SRj，即当li,j= 0时，记bi,j= 0。

3)干扰距离矩阵θ={θi}, 1≤i≤M，用实数表示不同授权频段的干扰阈值大小，是关于授权频谱干扰阈值的一维向量。其中，θi表示授权频段 SRi所能忍受的干扰阈值。

4) 干扰矩阵C用三维矩阵C={ci,j,k}M×N×N表示任何2个认知用户在共享某一授权频谱资源时的干扰度。其中，行标i代表授权频段SRi，j，k分别代表认知用户CRj和认知用户CRk。

同时，与CSGC算法只是简单地用0,1表示干扰矩阵元素值的方法不同，本文用区间[0,1]内的实数值代替干扰矩阵的元素值。若认知用户无法同时接入某一授权频谱，则认为这些认知用户在该频谱上的干扰度为 1；如果认知用户可以共享某一授权频谱，且认知用户之间的距离小于对应授权频谱的干扰距离，则令认知用户在该频谱上的干扰度为干扰距离与实际距离的比值；相反，如果认知用户之间的距离大于该授权频谱的干扰距离，则令认知用户在该频谱上的干扰度值为0。

5) 分配矩阵A记录了频谱分配算法的运行结果，用矩阵A={ai,j|ai,j∈{0, 1}}N×M表示，1≤i≤N,1≤j≤M。如果认知用户CRi分配到频谱资源SRj，则记ai,j=1；否则，ai,j= 0。

根据上述数学描述，可以把认知无线电网络抽象成图论模型G=(V,E,B)。顶点V代表认知用户集合；边的集合E记录能够同时接入某一授权信道时发生干扰的2个认知用户之间的关系；集合B表示各个顶点可选的颜色集合(即可用频谱资源列表)和各个颜色所对应的权重(即频谱效益)。

4 基于干扰消减的频谱分配算法

为了充分利用可用频谱资源，保证能够共享同一频谱资源的认知用户数量最大化，本算法首先对可共享同一频谱资源的认知用户进行频谱分配，然后再将剩余的可用频谱资源分配给尚未获得频谱资源的认知用户。

根据可用矩阵L和干扰矩阵C的定义，可以得到以下结论。

定理1 当li,m+lj,m≤1时，必定满足cm,i,j=0。

定理2 当cm,i,j=1时，认知用户CRi和认知用户CRj在共同使用授权频谱SRm时产生干扰，且必定存在li,m=lj,m=1。

定义能够接入同一授权频段而不发生干扰的 2个认知用户为共享用户对。可以发现，当且仅当li,m+lj,m＞1，且cm,i,j=0时，认知用户CRi和认知用户CRj可以共享授权频谱SRm，构成一个共享用户对，记为＜CRi, CRj＞。

由于认知用户在指定频段下的干扰关系是对称的，将干扰矩阵C指定频谱下三角部分值为0的元素置为1，将值为1的元素置为0，除去对角线上的元素后，可以得到所有值为1的元素所对应的行标和列标构成了该频谱下的所有共享用户对。

然而，由于认知用户可能处于多个授权频谱的覆盖范围之内，多个共享用户对在接入同一授权信道时可能存在相互干扰，以及不同共享用户对中出现认知用户重叠。为了充分利用频谱资源，必须对共享用户对进行再次优化，得到能够共享某一授权频谱资源的最多认知用户集合。因此，本文进一步将能够同时共享同一频谱的所有认知用户所组成的集合定义为在该频谱下的最大共享独立集；记授权频谱SRm的最大共享独立集用Gm表示。

为了最大化地利用授权频谱资源，必须找出每个频段中互不产生干扰的所有认知用户，并获取各个授权频谱对应的最大共享独立集。因此，本算法首先对各个频谱下的所有共享用户对进行遍历。

假设＜CRi, CRj＞为频谱SRm下的共享用户对。在遍历过程开始时，可以认为授权频段SRm的最大共享独立集的初始值Gm={CRi, CRj}。

假设授权频段SRm的所有共享用户对中存在认知用户 CRk，1≤k≤N,k≠i,k≠j，且定义认知用户CRk的冲突度为该节点与频谱SRm的当前最大共享独立集Gm中元素发生干扰的数量。

可以发现，认知用户CRk与当前最大共享独立集Gm可能存在以下3种场景，如图2所示。图中，圆圈中的字母i，j，k分别表示认知用户CRi，CRj和CRk，字母m表示频谱资源SRm；实线表示其两端的认知用户在使用频谱资源时存在干扰，而虚线表示其两端的认知用户可以同时共享该频谱资源。

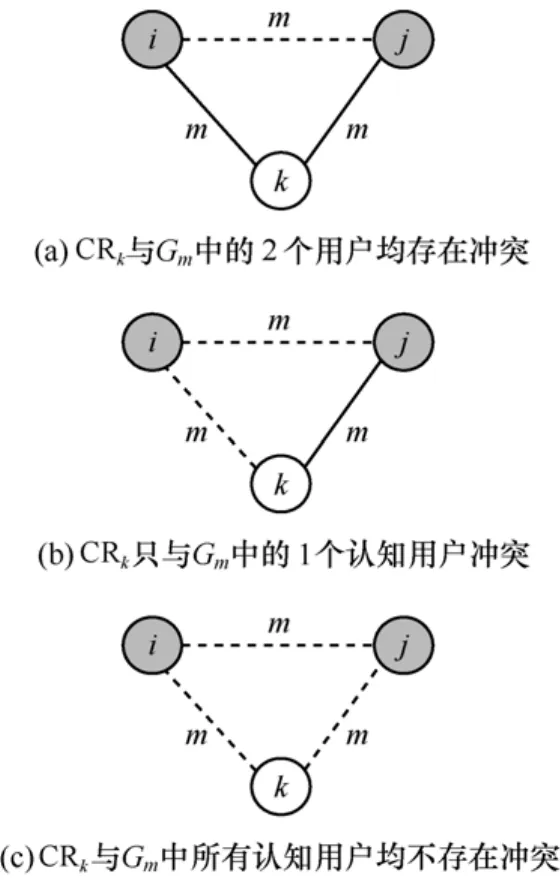
图2 授权频谱SRm下的认知用户共享冲突

为了构建最大共享独立集，本算法针对以上 3种情况进行了区分处理。

1) ∀CRi∈Gm，CRj∈Gm，i≠j，且∃cm,i,k=1，cm,j,k=1

认知用户CRk与共享独立集Gm中的2个认知用户CRi、CRj均存在冲突，如图2(a)所示。CRk与集合Gm的冲突度为2，集合Gm内的元素保持不变。

2) ∀CRi∈Gm，i≠j，且∃CRj∈Gm，满足cm,i,k=0，cm,j,k=1

认知用户CRk只与独立集Gm中的一个认知用户存在冲突，即CRk与集合Gm的冲突度为1，如图2(b)所示。此时，本算法将比较认知用户 CRj和认知用户 CRk在频谱 SRm下产生的频谱效益。若bj,m＞bk,m，则集合Gm保持不变；否则，以认知用户CRk替换认知用户 CRj，Gm=Gm－{CRj}+{CRk}。

3) ∀ CRi∈Gm，满足cm,i,k=0

此时，认知用户CRk与独立集Gm中的所有认知用户均不存在冲突，即CRk与集合Gm的冲突度为 0，如图 2(c)所示。此时，本算法将把认知用户CRk归入频谱 SRm的最大共享独立集，即Gm=Gm+{CRk}。

以上过程不断迭代，直至所有的共享认知用户遍历结束，得到频谱SRm的最大共享独立集。

由于最大共享独立集中的认知用户在接入同一频谱时不存在相互干扰，为了有效利用频谱资源，本算法优先为含有认知用户数量最多的最大共享独立集中的认知用户分配频谱，即将频谱资源同时分配给最大共享独立集中的所有认知用户。

设独立集Gmax={CRi, CRj, CRk,…}为包含最多认知用户的最大共享独立集，且SRmax为该集合所对应的频谱资源。根据本算法的执行原理，首先将频谱SRm分配给独立集Gmax中的所有认知用户，并在分配矩阵A中设置相应的频谱分配结果，即令：

同时，更新集合Gmax中所有认知用户在可用矩阵L中的频谱可用性，将可用矩阵L中的对应行元素置为0。即

∃CRi∈Gmax, ∀m, 1≤m≤M,m≠max，则令li,m=0

为共享独立集Gmax中的认知用户分配完频谱资源后，本算法将继续查找频谱 SRmax下与集合Gmax中认知用户产生冲突的所有认知用户，并更新其在频谱SRmax下的可用状态。即

本文对温州南站中央空调主机进行智能节电系统改造，使用环境温度保持与原来进行节能改造前完全一致的情况下，改造后可以获得收益：

对于∀n, 1≤n≤N, 且 CRi∈Gmax，若∃cmax,i,n= 1,则令ln,max= 0。

然而，由于认知用户可能被多个授权频谱所覆盖，同一个认知用户可能出现在不同授权频谱的最大共享独立集中。因此，本算法进一步对频谱分配过程进行优化，将已分配到频谱资源的认知用户从其他授权频谱的最大独立共享集中删除。即

对于∀m，1≤m≤M，m≠max，若∃CRi∈Gmax，且 CRi∈Gm，则Gm=Gm－{CRi}

以上过程不断迭代，直至将所有已分配到频谱资源的认知用户从其他授权频谱的最大共享独立集中删除为止。

为能够共享频谱的认知用户分配频谱后，本算法将进一步为未分配到频谱资源的其他认知用户分配频谱资源。令已分配到频谱资源的认知用户集合为GI= {CRi, CRj, CRk, …}，且所有未分配到频谱资源的认知用户集合为GII={CRx, CRy, CRz, …}。

在为集合GII内的认知用户分配可用频谱时，剩余的可用频谱将随着频谱分配过程的进行而不断变化。为此，本文进一步定义认知用户在未进行频谱分配时的可用频谱为该认知用户的初始可用频谱；同时，定义干扰度Dx,m为在集合GII内的认知用户CRx与其他认知用户在频谱SRm中产生的干扰量。

结合效益矩阵B和干扰矩阵C，可以得到所有未分配到频谱资源的认知用户的初始可用频谱和干扰度。即对于∀m，1≤m≤M，∃CRx∈GII时，可以得到以下结论。

结论1 当bx,m=0时，频谱SRm不是认知用户CRx的初始可用频谱，且认知用户CRx在频谱SRm下的干扰度为0。

令number(CRx)为认知用户 CRx的可用频谱数量，结合可用矩阵L可以得到number(CRx)为

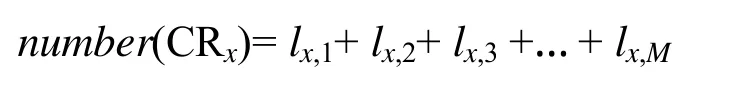
通常，可用频谱数量较多的认知用户获得频谱的概率相对较高。为了保证更多的认知用户可以接入授权频谱，本算法将从集合GII中优先选择可用频谱数量最少的认知用户进行分配，直到所有认知用户被遍历，或者所有频谱资源被分配为止。

令CRmin为所有未分配到频谱资源的认知用户中可用频谱数量最少的认知用户，且其可用频谱数量s为

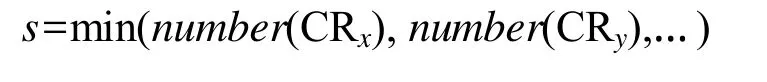
同样，根据s值的不同，本算法将对认知用户CRmin进行区分处理。

1) 若s=0，即认知用户CRmin无可用频谱资源

此时，认知用户CRmin接入任何一个初始可用频谱都会对其他已分配到频谱资源的认知用户产生干扰。即对于∀m, 1≤m≤M，Dmin,m≥θm。

根据Dmin,m与θm的关系，又可以分为2种情况。

a) 对于∀m, 1≤m≤M,bmin,m＞0，若干扰度Dmin,m＞θm，则GII=GII－{CRmin}，本算法将不再为认知用户CRmin分配频谱资源；

b) 对于∀m, 1≤m≤M,bmin,m＞0，以及 CRi∈GI，若∃Dmin,m=θm，cm,i,min=1，且bmin,m＞bi,m，则将频谱资源SRm分配给认知用户CRmin，取消认知用户CRi对频谱SRm的使用权，即置ai,m=0，amin,m=1；此时，对认知用户CRmin的分配结果不会对其他认知用户造成影响。

2) 若s=1，即仅有唯一的频谱资源可供认知用户CRmin接入

本算法将把该频谱资源分配给认知用户CRmin，即对于∀m, 1≤m≤M, 若∃lmin,m=1，令amin,m=1。

3)s＞1，即认知用户CRmin可以在无干扰的情况下接入多个可用授权频谱

可用矩阵L中存在lmin,1+lmin,2+…+lmin,M＞1。此时，本算法将找到能够使认知用户CRmin产生最大频谱效益的频谱SRm，并将频谱SRm被分配给该认知用户。即∃m, 1≤m≤M, 且lmin,m=1，使得bmin,m=max(bmin,1×lmin,1,bmin,2×lmin,2,… ,bmin,M×lmin,M)， 则 令amin,m=1。

同时，本算法将继续更新可用矩阵L，将已分配到频谱资源的认知用户所在行的元素置为0。即

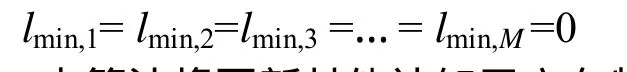
另外，本算法将更新其他认知用户在频谱SRm中的可用状态，即对于∀x, 1≤x≤N, 如果∃CRx∈GII,且∃cm,min,x= 1, 则令lx,m= 0。

最后，将已分配到频谱资源的认知用户从集合GII中删除，并将已分配到频谱资源的认知用户添加到集合GI中。即

以上分配过程不断迭代，直至集合GII为空或所有授权频谱资源被分配完为止。

本算法的核心伪代码如图3所示。

当前，可以通过集中式和分布式2种方式来实现上述频谱分配过程。

1)集中式

如果认知无线电网络中存在一个中心调度节点负责为所有认知用户分配频谱资源，则本算法的实施过程将非常直接。中心调度节点收集图中所有节点的可用频谱、频谱效益、接入干扰等信息，并执行本文所提出的频谱分配算法，将分配结果反馈给所有认知用户。

图3 算法的核心伪代码描述

2)分布式

认知无线电网络中的各个节点将向其所有邻居节点发送位置、可用频谱、频谱效益等信息，各节点分别构建全网可用矩阵、效益矩阵和干扰矩阵。通过执行本文提出的干扰消减算法，各个节点将各轮分配结果反馈给其邻居，并更新分配矩阵、可用矩阵。该步骤不断迭代，直到所有频段资源被分配或者所有认知用户都得到可用频谱为止。

5 算法性能分析及仿真实验

根据前文所述，CSGC算法为了确保系统频谱效益，在频谱分配过程中优先将频谱资源分配给标号最大的认知用户，其算法复杂度为O(n2)。本文提出的IESA算法则需要首先找到能够共享同一频段的多个认知用户进行频谱分配，然后再对未分配到频谱资源的认知用户进行频谱分配，算法复杂度为O(n2)。因此本算法在复杂度上相对于CSGC算法并未有实质性的增加。

目前，对认知无线电频谱分配算法的性能评估主要从系统频谱效益和网络公平性等角度进行。

1)系统频谱效益是指所有分配到频谱资源的认知用户在相应频段上贡献的频谱效益总和。

利用分配矩阵A与效益矩阵B，可以得到频谱分配过程结束后所取得的系统频谱效益Usum。

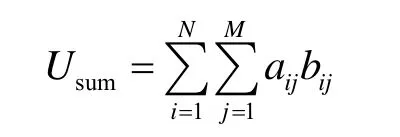
2) 网络公平性则体现了将频谱资源分配给认知用户的均衡程度[9]。

可以发现，网络公平性pa可由用户分配率表示，即所有分配到频谱资源的认知用户占系统认知用户总量的比例。其计算方法如下：

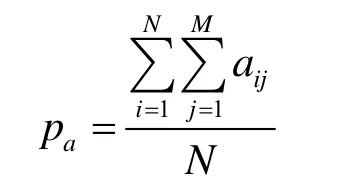
为了验证IESA算法的运行性能，本文分别对认知用户数量多于和少于授权频谱总量的场景进行了分析。本文采用Java语言对IESA算法与CSGC算法进行了模拟实现，对2种算法的系统频谱效益和网络公平性等性能指标进行了比较。在模拟过程中，各个授权频谱的频谱空穴随机生成，认知用户之间的干扰度由处于同一授权频段的认知用户之间的距离和授权频谱的干扰阈值决定。

图4给出了IESA算法和CSGC算法在授权频谱数量为 10的认知无线电网络中所对应的用户分配率。可以看出，当认知用户数量大于可用频谱总数时，CSGC算法和IESA算法对认知用户的满足程度随着认知用户数量的增加而下降，但IESA算法在整个模拟过程中相对CSGC算法能够满足更多认知用户的频谱接入。当M=10，N=35时，CSGC算法的用户分配率仅为65%，而IESA算法能够使85%的认知用户获得频谱资源。

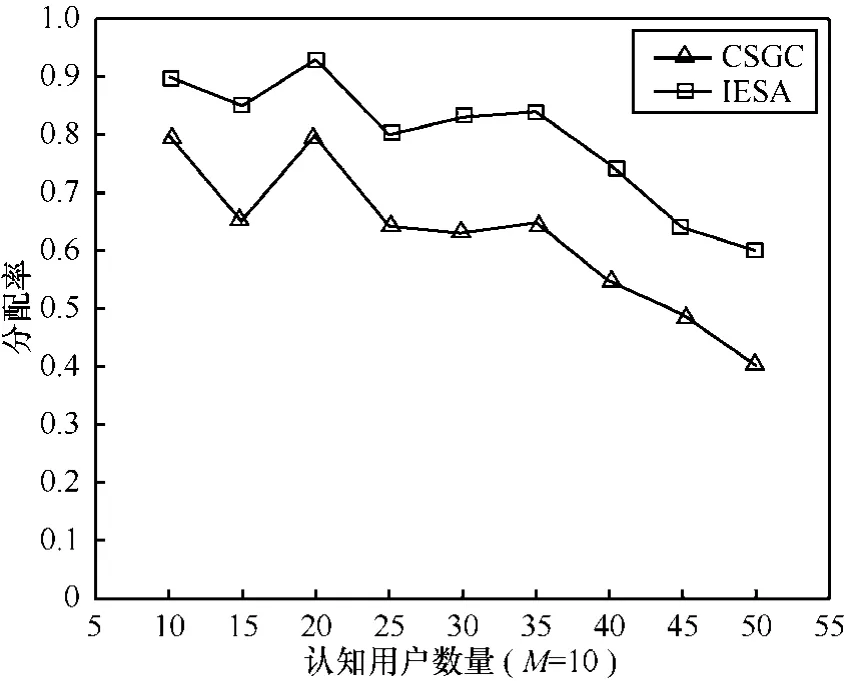
图4M为10的用户分配率

与此同时，图 5给出了 2种频谱分配算法在M=10时的系统频谱效益。可以看到，2种算法的系统频谱效益随着认知用户数量的增加而不断递增。当认知用户数量小于20时，CSGC算法可以获得较好的系统频谱效益。然而，当认知用户数量大于20时，IESA算法的系统频谱效益相对较优。可以得到，当认知用户数量多于可用授权频谱总数时，IESA算法可以在获得较好认知用户接入数量的同时，取得较优的系统频谱效益。

图5M为10的系统频谱效益

当授权频谱数量增加到50，且认知用户的数量从10增加到50时，实验得到2种算法对用户的分配率均为 100%。因此，当认知用户数量小于系统的可用频谱总数时，IESA算法相对CSGC算法在认知用户接入数量方面并没有表现出一定的优势。

图6给出了2种频谱分配算法在授权频谱总数大于认知用户数量时所取得的系统频谱效益。当授权频谱总数为 50时，随着认知用户数量的不断增加，CSGC算法所获得的系统频谱效益一直呈上升趋势，且均高于IESA算法所获得的系统频谱效益。并且，在认知用户数量增加的过程中，IESA算法的系统频谱效益波动较大。

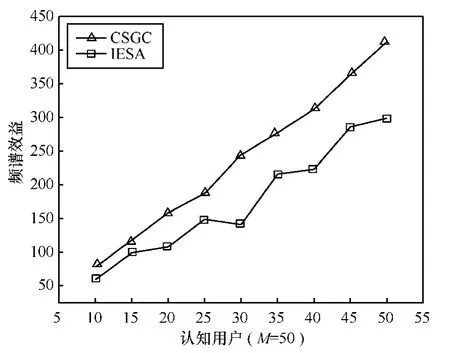
图6M为50的频谱效益

为了进一步验证IESA算法，本文继续使用Jing Zhong和Jialiang Li于2009年开发的认知无线电仿真模块CRCN[10]对NS2进行了扩展，并分别完成了CSGC算法和IESA算法在NS2下的仿真实验。

本文主要针对CSGC算法和IESA算法的分组传输时延、分组丢失率、信道干扰量和网络吞吐量等参数进行分析。在仿真实验中，10对认知用户在1 000×1 000的区域内感知并接入3条授权信道进行FTP通信。认知节点的地理位置随机生成。

图7给出了2种频谱分配算法的实时信道干扰量仿真结果。可以看出，IESA算法中的认知用户在接入相同授权信道的干扰量与CSGC算法的干扰量差别不太明显，仅在仿真过程的开始阶段和结束阶段有细微的差别。在3s～7s期间，2种频谱分配算法的干扰量大致相同。IESA算法在仿真初期的信道干扰量相对较高；在仿真结束阶段，CSGC算法的信道干扰量相对较高。

图7 实时信道干扰量

图8给出了2种频谱分配算法在发送第800个到第8 000个数据分组过程中被正确接收的数据分组的实时累积时延。由于IESA算法是基于冲突消减的分配算法，且在同一信道中来自不同节点的数据分组的冲突退避时间较短，数据分组从发送到接收的累积时延都较小。可以看出，在整个仿真过程中IESA算法相对于CSGC算法在传输过程中引入的延迟较低。当数据分组传输数量达到6 400个时，IESA算法的累积延迟才超过CSGC算法。

图9给出了CSGC算法和IESA算法在不同时间段内的传输分组丢失率。可以看到，在仿真初始阶段，各个认知用户间由于尚未建立起通信连接，认知用户发送或接收到的 RTS/CTS控制分组数量较多；同时，由于多个FTP业务的启动时间相对一致，认知用户之间的控制分组发生冲突的概率较大，网络应用在2种频谱分配算法的仿真初期分组丢失率均相对较高。当t=4s时，CSGC算法的分组丢失率达到最大。传输过程启动5s后，不同授权信道上的数据分组不断积累，导致2种频谱分配算法的平均分组丢失率略呈上升趋势。可以发现，在整个仿真过程中IESA算法的平均分组丢失率都低于CSGC算法。

图8 分组传输的累积时延

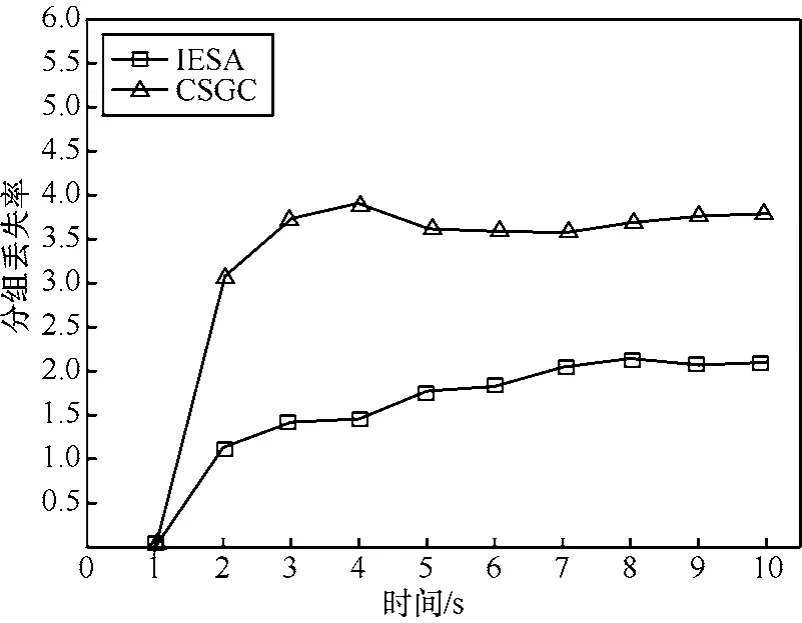
图9 通信过程中的分组丢失率

图10给出了运行CSGC算法和IESA算法的认知无线电网络在仿真过程中的实时吞吐量。与传输分组丢失率的分布类似，通信初期由于大量控制分组的交互，网络吞吐量在短时间内急剧增长。当t=4s时，IESA算法的吞吐量达到最大值；由于IESA算法在认知用户数量明显多于授权信道数量时能够满足更多的认知用户的接入需求，在整个仿真过程中，IESA算法都能取得比CSGC算法更好的运行性能。

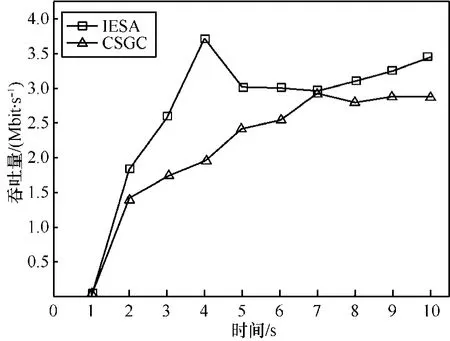
图10 不同时间段的网络吞吐量

综合上述分析和仿真结果可以看出，CSGC算法的目标是在避免干扰的前提下，最大化认知无线电网络的频谱效益。在认知用户的接入数量和频谱效益之间，CSGC算法更加侧重于认知用户利用所分配到的频谱资源所获得的最大频谱效益。IESA算法则综合分析了不同认知用户的频谱共享程度和可用频谱数量，以最大化认知用户接入数量为目标。因此，CSGC算法适合于频谱资源数量较多或系统对频谱效益要求较高的场景；而 IESA算法则适合于对认知用户接入数量要求较高的场景或认知用户数量明显大于授权频谱总数的场景。

6 结束语

本文在综合分析了认知无线电网络频谱接入、频谱干扰的基础上，提出了一种基于干扰消减的认知无线电频谱分配算法。该算法通过检测能够共享同一授权频段的所有认知用户，优化了接入授权频谱的认知用户数量。同时，该算法对未获得频谱资源的认知用户按照其可用频谱数量进行特殊处理，保证了频谱分配过程的公平性。

模拟和仿真实验结果表明，该算法能够在认知用户数量较多、可用频谱紧张的情况下对认知无线电网络的频谱分配过程进行优化，能够增加接入授权频谱的认知用户数量，在一定程度上提高认知无线电网络的频谱效益。

[1] STAPLE G, WERBACH K. The end of spectrum scarcity [J]. IEEE Spectrum, 2004, 41(3):48-52.

[2] 孟祥初. 通信产业网[EB/OL]. http://www.ccidcom.com/html/chanpinj- ishu/wuxiantongxin/200911/02-80768.html,2009.MENG X C. The usage survey of wireless spectrum[EB/OL].http://www.ccidcom.com/html/chanpinj-ishu/wuxiantongxin/200911/02- 80768.html,2009.

[3] JOSEPH M III, Cognitive radio for flexible mobile multimedia communications [J]. MONET, 2001, 6(5):435-441.

[4] WANG W, LIU X. List-coloring based channel allocation for open-spectrum wireless networks[A]. Proc of the 62nd IEEE Vehicular Technology Conference[C].Dallas, texas, USA, 2005. 690-694.

[5] ZHENG H, PENG C. Collaboration and fairness in opportunistic spectrum access[A]. Proc of the 2005 IEEE International Conference on Communications[C]. Beijing, China, 2005. 3132 -3136.

[6] TANG J, MISRA S. Joint spectrum allocation and scheduling for fair spectrum sharing in cognitive radio wireless networks[J]. The International Journal of Computer Networks, 2008, 52(11):2148-2158.

[7] HOANG A, LIANG Y. Maximizing spectrum utilization of cognitive radio networks using channel allocation and power control[A]. IEEE 64th Vehicular Technology Conference[C]. Singapore, 2006. 1-5.

[8] XIE X, ZHOU T, DONG X. Traffic-demand dynamic spectrum access[A]. Proc of the 4th International Conference on Wireless Communications, Networking and Mobile Computing[C]. Chongqing,China, 2008.1-4.

[9] AHMED W, GAO J, FAUKNER M. Channel allocation for fairness in opportunistic spectrum access networks[A]. Proc of the 2010 IEEE Wireless Communications and Networking Conference[C]. Sydney,Australia, 2010.1-6.

[10] 林闯,李寅,万剑雄. 计算机网络服务质量优化方法研究综述[J].计算机学报,2011,34(1):1-14.LIN C, LI Y, WAN J X. Optimization approaches for QoS in computer networks: a survey[J]. Chinese Journal of Computers, 2011,34(1):1-14.

[11] Cognitive radio cognitive network simulator[EB/OL]. http://stuweb.ee.mtu.edu/～ljialian/.