基于Modelica技术的Dante谱仪解谱建模仿真
2012-08-03李海艳李维嘉黄运保艾翠蓉
李海艳,李维嘉,黄运保,艾翠蓉
(1.华中科技大学船舶与海洋工程学院,湖北 武汉 430074;2.三峡职业技术学院机械制造系,湖北 宜昌 443003)
惯性约束聚变实验(如ICF)已经成为人类探索新能源的重要实验手段之一[1-3]。实验中,会产生大量的实验数据且需要分析大量实验结果。目前的处理方法多为单独的编程程序[4-5],重用度低,集成度不高,并且接口不一,不同实验课题组之间很难交流,编程工作重复性强,知识无法积累。采用多领域仿真与建模语言Modelica[6]进行ICF实验数据处理的建模,能够使模型按照统一的标准进行组织,可读性高,若将建好的模型加入到Modelica标准库中,能实现数据处理各功能模块的积累和重用。国外早在20世纪70年代就已经建成了完整的ICF实验数据处理分析系统,并且开展了ICF数值模拟实验,而我国才刚刚起步。实验数据处理系统模型是模拟实验的重要组成部分,通过对实验光源、设备、仪器的建模,最终可实现Modelica平台上完整的ICF模拟实验,我国的ICF实验研究将进入一个新的阶段。
对激光聚变诊断的目的在于通过对等离子体辐射和聚变反应产物的特性测量来揭示靶等离子体的状态和行为,更深入地了解激光能量的吸收机制和规律特性,为激光与靶的最佳耦合设计提供依据。在ICF实验中,激光等离子体发射较强的X光辐射,其能谱主要集中于软X光能区(0.1~1.5 keV),它的总能量、能谱特征、发射时间过程和空间分布都是理论和实验所极为关心的基本数据,其中包含了等离子体参加聚爆过程的大量信息,尤其是软X光能谱直接相关于X光转换率和辐射温度这两个关键物理量[7],因此软X光谱的测量是ICF诊断中至关重要的内容。14通道软X光能谱仪是测量软X射线能谱、等效积分温度和辐射能流时间过程的诊断设备。因其响应覆盖的能量范围较宽,且互相重叠,同时又是多通道谱仪,谱还原存在一定的难度。基函数法[8-10]是还原能谱分布的一种常用方法,而采用三次B样条基函数对谱型的还原能力最强。
笔者采用Modelica语言使用三次B样条基函数法对14通道软X光谱仪解谱过程进行建模,并进行仿真观察结果,以验证使用Modelica进行ICF实验数据处理平台建模的可行性。
1 Modelica语言
Modelica是一种为了解决多领域物理系统统一建模与协同仿真而提出的面向对象的陈述式建模语言。Modelica语言对来自不同领域的系统构件采用统一的数学方程进行描述,基于语言内在的组件连接机制实现模型的构成和不同领域模型的集成与数据交换。通过求解微分方程或代数方程描述问题,实现建模和仿真。基于Modelica语言来实现复杂的建模与仿真具有建模方便,模型重用度高,模型库知识强大,灵活性强,模型与仿真相对独立等优点。基于这些特性,Modelica语言已经被越来越广泛地运用到机械、电子、控制、能源等领域,建立了开放的可重用的可视化模型和各领域的模型库,实现了领域知识的重用。
使用Modelica进行ICF实验数据处理系统建模的优势在于:模型按照Modelica语言的标准构建,其搭建和运行仿真不依赖于具体的软件平台。当进行跨领域跨课题组的团队合作时,按照Modelica语言这个统一标准创建的模型,较之以前所使用的各自单独编写功能函数代码而言,大大提高了可读性,从而不依赖于程序的编写者,方便人员沟通交流与模型的重用。模型组件创建好后,可以加入到标准库中,随着标准库的不断丰富和完善,可实现整个ICF实验建模的知识积累。
2 基函数解谱求解方法
2.1 基函数解谱方法原理
在了解源谱特征的前提下,适当选取基函数,使用N个基函数的线性组合来近似源谱:
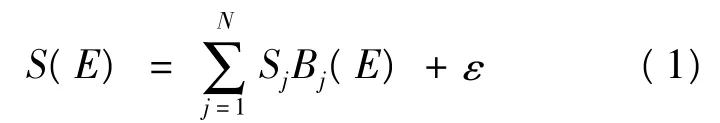
其中:S(E)为能谱分布;Bj(E)为第j个基函数(j=1,2,…,N)。基函数采取根据软X光谱仪各通道能谱响应而确定的三次非均匀B样条基函数。示波器的第k通道的电压为:

其中:M为通道数;Rk(E)为第k通道的能谱响应。将式(1)代入,有:就可以得到系数Sj,从而得到谱源分布。
吉林大学的刘建芳等人研制了一种双向推动式压电步进精密驱动器,如图8所示[14-15],该驱动器由导轨输出位移,可实现高频率(40 Hz)驱动,运动速度可达到0.24 mm/s,行程25 mm,最大输出力为47 N。

2.2 求解步骤
2.2.1 确定节点向量
(1)读入各通道数据文件(500个值)。
(2)找出每个通道响应的最大值a0,以该值的50%为标准值,找到最大值前、后与该标准值最近的点a1与a2,即每个通道保存3个值:a0,a1,a2。按照各个通道最大值所对应的横坐标值,对各通道进行排序,排序后,取第一个通道a1与
令Rkj=∫Bj(E)Rk(E)dE为第j个基函数与第k个通道响应函数相互作用的权重,代入式(3)中,通过求解线性方程组a2的横坐标值,其余通道取a2的横坐标值,这样共得到15个节点。
(3)按照前两个节点间隔和末两个节点间隔分别向前、后各扩展两个节点,共得到19个节点,再进行升序排序,得到节点向量序列。
2.2.2 求基函数
(1)由节点向量序列生成三次非均匀B样条基函数。
(2)将通道响应的500个能量值(即横坐标)分别代入第j个(j=1,2,…,14)基函数中,得到Bj(E)。
2.2.3 积分求第i个通道与第j个基函数作用的权重
其中:Rik为第k个通道响应数据中第i个值;Bij为通道响应中第i个横坐标在第j个基函数作用下的值。
2.2.4 最小二乘法解线性方程组
2.2.5 求出谱源分布
(1)对于第j个基函数,将Bj(E)中每个值Bij与Sj相乘 ,得到结果设为Mij。
(2)对Mij按 j求和,即,所得Si即为解谱结果S(E)。
(3)绘制谱源分布的曲线图得到谱形。
3 解谱过程Modelica建模
3.1 模型连接
各个模型之间通过连接器Connector连接。连接器定义了输入输出的变量,数据在各个模型之间通过连接器进行通信。在该次建模中定义了InPort、OutPort、InPortMatrix、OutPortMatrix 4 个连接器,分别用于数组和矩阵的输入输出连接。
3.2 模型层次划分
在Modelica语言中按照由下至上的建模方法搭建模型。根据模型的复杂程度确定划分的层次,最大限度地使模型清晰易读。为了提高重用度,首先要提炼出一些通用的模型单独列出以供调用。例如每个模型包含与其他模型连接的接口,接口具有通用性,并且部分模型不能作为独立模型进行仿真,因此单独划分为底层模型Interface。第二层Blocks中的模型每一个都可以独立使用,能够单独完成某一项功能,作为功能模块被更高层中的模型调用,根据这个标准来创建各个Blocks中的模型。第三层Parts中的模型全部由Blocks中的模型搭建而成,按照数据量的需要合并多个同一功能模型,按照功能的相关性合并不同功能的模型。Parts层中的模型具有组合功能,集成度高,以使最终数据处理模型的功能模块简洁,处理步骤清晰明了。模型层次结构划分如图1所示。

图1 模型层次结构划分
由图1可知,该次建模的Interface层,根据数据处理的输入输出数据量需要和数据的类型创建不同的接口Interface模型。例如两个数组输入一个数组输出(MI2MO)用于两数组对应值进行加减乘除运算;两个数组输入两个数组输出(MI2MO2)用于对两个数组同时进行排序;两个数组输入单个数据输出(MI2SO)用于对两个函数乘积进行积分;一个矩阵一个数组输入一个数组输出(MImatrixMIMO)用于通过输入系数矩阵和列向量值求解线性方程组。Blocks层中模型按照所实现的单一功能来创建。包括读入数据文件模型DataTable,取最大值模型 ChannelDataMax,排序模型 SortMaxData,生成节点向量模型 Create-KnotVector,生成三次 B样条基函数模型Bspline3,积分模型Integrate,最小二乘法求解线性方程组模型LeastSquares等。为实现各个模块需要的功能,还需要创建一些函数,以方便不同模块中相似功能的调用。对于简单的功能例如合并、积分等可以直接在Modelica中编写算法;对于复杂的功能例如生成三次B样条基函数和最小二乘法求解线性方程组,则通过调用C语言或Fortran语言编写的外部函数来实现。Parts层中的模型全部由Blocks层模型搭建而成,由于该次建模的软X光谱仪采用14通道,通道多,数据量大,因此有必要对多个单一功能模块进行组合和合并,Parts层模型按照所实现的功能依次对Blocks中的模型进行组合,最终的实验模型就可以按照功能模块划分,由几个简单的Parts模型搭建而成,其模块功能划分如图2所示。

图2 模块功能划分
3.3 时间关联模型
该次实验的数据处理模型是与时间无关的模型。而在仿真时要显示出结果数据的曲线图,根据仿真时间进程模拟横坐标,结果数据值为纵坐标,绘制出结果曲线。因此,创建了一个模型Yt_Signal用于仿真时将数据与时间相关联,它的方程为:

其中:nin为数组中的数据量;time为仿真过程时间变量;end_time为仿真截止时间。在仿真时,绘制任何函数的等间距采样曲线图都可以调用这个模型。
4 仿真实例及结果
为了验证笔者方法的可行性,通过以上模型组件以Matlab为平台搭建一解谱模型如图3所示。
设置仿真时间可通过对其仿真得到的谱源能量分布曲线用Matlab仿真得到,如图4所示,实线为原始的谱源能量分布曲线,点划线为实验得到的曲线。由图4可知,实验谱源曲线与理论谱源曲线基本一致。
5 结论
笔者针对惯性约束聚变(如ICF)实验的数据处理过程中数据量大,学科交叉,项目课题多的特点,提出了使用Modelica语言进行数据处理过程建模的思想,并完成了软X光谱仪基函数解谱法的Modelica建模和仿真。仿真得到的结果基本与理论解谱结果一致。为使结果精确度更高,可在求解基函数前对节点向量进行优化,使得响应矩阵的条件数最小,结果更接近真实值。从通用模型组件的创建和调用中可以看出,ICF实验数据处理在Modelica平台建模过程中能够使处理方法得到较好的积累与重用。

图3 解谱模型

图4 解谱仿真结果比较
[1] 宋天明,杨家敏,易荣清.ICF实验软X光谱能的基函数解谱法[J].强激光与粒子束,2010,22(12):2905-2910.
[2] 江少恩,郑志坚,孙可煦.软X光能谱仪的一种新的解谱方法[J].计算物理,2001,18(3):276 -280.
[3] 杨存榜,虞孝麒,苏春晓,等.用于ICF实验的大型数据库系统的开发[J].核电子学与探测技术,2002,22(1):32 -35.
[4] 唐永健,孙可煦,徐和平,等.激光等离子实验中的低能X射线时间谱解谱方法[J].强激光与粒子束,1991,3(4):483 -492.
[5] 刘成海,陆正强.激光核聚变中X光解谱方法的光滑化技术[J].计算物理,1985,2(3):313 -320.
[6] ELMQVIST H,MATTSSON S E,OTTER M.Object- oriented and hybrid modeling in modelica[J].Journal Européen des Systèmes Automatisés,2001,35(1):1 -15.
[7] 孙可熙,易荣清,黄天喧.软X光能谱仪探测元件响应曲线标定[J].高能物理与核物理,2001,25(5):448-454.
[8] 杨家敏,丁耀南,郑志坚,等.高谱分辨X光能谱诊断技术[J].强激光与粒子束,2003,15(1):69 -72.
[9] PRESS W H,TEUKOLSKY S.Numerical recipes in C:the art of scientific computing[M].England:Cambridge University Press,1997:18 -98.
[10] D'AGOSTINI G.A multidimensional unfolding method based on Bayes’theorem[J].Nuclear Instruments and Methods in Physics Research A,1995(362):487 -498.
