供应链客户流失风险预测模型研究

喻 立

(清远职业技术学院外语与经贸学院，广东 清远 511510)

供应链管理强调企业间的动态协同和敏捷响应，在向客户提供产品或服务的过程中，供应商需要通过与客户的互动充分了解客户，把握客户的动态需求，提供极具价值的个性化服务解决方案，从而为企业带来高额的服务利润。但对大多数供应商来说，出于资金或技术方面的原因，这种“以客户为中心”的拉动式管理模式在实施上仍然具有相当的难度，产品的同质化和客户需求的日益多样化加剧了供应链管理环境的复杂性，这使得客户对所提供的产品或服务很难产生持久的依赖和忠诚，如果不引起警觉，将会造成客户的大量流失。笔者试图运用神经网络理论构建供应链客户流失风险预测模型，帮助供应链企业准确预测处于流失风险状态的客户，从而采取有针对性的措施保留现有客户，提升供应链的整体盈利能力。

现有研究中关于供应链客户流失风险的预测模型普遍存在计算量大、准确性低等缺点，人工神经网络(artificial neural networks)是对人脑或自然神经网络(natural neural network)若干基本特性的抽象和模拟，其优越性体现在它具有强大的自学习功能和高速寻找优化解的能力[1－3]。基于神经网络的供应链客户流失风险的预测是一个寻求复杂问题优化解的过程，运用神经网络可以构建非线性的预测或分类模型，具有较高的准确度，尤其在条件局限的情况下，即使数据集没有达到理想的数量，仍然可以构建出符合要求的预测模型。

1 神经网络相关理论

神经网络是由大量的神经元相互连接而成的网络，神经元一般表现为一个多输入、单输出的非线性器件。其结构模型如图1所示，x为神经元的输入;w为连接弧的权值，在神经网络的学习训练中，w会不断进行适应性调整并发生变化;为对所有的输入值与对应的权值相乘后加总;f(ui)为传递函数，一般是非线性函数，其目的是映射到输出。

图1 神经元结构模型

神经元传递输出函数有Sigmoid函数、logistic函数、双曲正切函数、线性型函数和阈值型阶跃函数等，其中Sigmoid函数构成的人工神经网络结构较为复杂，但Sigmoid函数是递增的，其导数不为零，因此比其他几种激励函数有更好的特性[4]。

(1)阈值型阶跃函数为:

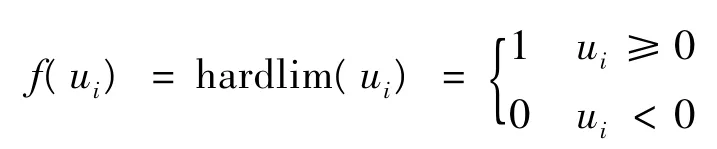
(2)线性型函数为:

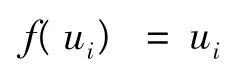
(3)Sigmoid函数为:

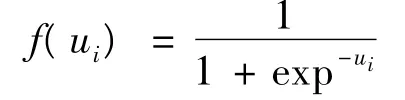
根据神经元之间连接方式的不同，神经网络分为前向网络、有反馈的前向网络、层内有相互结合的前向网络，以及全互联型或部分互联型网络。基本的前向网络如图2所示，左右分别为输入层和输出层，中间为隐含层，神经网络至少包括3个层次，运用这种网络层次结构可以反映输入与输出之间的复杂非线性关系，BP神经网络采用的就是这种前向网络结构[5－6]。

图2 前向网络结构

不同的神经网络结构和模型应使用不同的学习规则来调整神经元之间的连接权重，实现神经网络的学习。神经网络的学习又称为网络训练，即从环境中获取知识改进自身性能，主要指调节网络权值和阈值参数，使网络以一种新方式对外部环境做出反应，通常有以下3种学习规则[7]。

(1)Hebb学习规则。输入输出同时兴奋时，相应的权值得到加强，其表达式如下:

(2)delta学习规则。根据输出节点的外部反馈来改变权系数，设输出层第k个神经元的实际输出为ak(n)，目标输出为tk(n)，则误差ek(n)=tk(n)－ak(n)，目标函数为基于误差ek(n)的函数，如误差平方和判据(sum squared error，SSE)，或均方误差判据(mean squared error，MSE)，则有:

其学习规则表达式为:

(3)竞争学习规则。根据神经元之间的输出决定权值的调整，输出神经元之间有侧向抑制性连接，较强单元获胜并抑制其他单元，其学习规则表达式如下:ΔWkj=η(pj－Wkj)，神经元 k获胜;ΔWkj=0，神经元k失败。

2 客户流失风险预测建模

2.1 问题描述

面对激烈的市场竞争，某企业所在供应链的终端客户流失率有大幅上升的趋势，通过对客户历史数据的统计分析，以下变量与客户流失风险存在较强的因果关系:A类业务平均交易额、B类业务平均交易额、客户满意程度、客户月平均交易次数和客户营业收入，如表1所示。

表1 供应链客户流失风险变量描述

案例中A类业务平均交易额、B类业务平均交易额、客户月平均交易次数和客户营业收入等数据可从客户历史数据库中直接获得，而客户满意程度指标则采用5级利科特量表(likert scale)，通过问卷调查和统计分析获得。由于这些数据具有不同的单位与量级，因此在数据输入神经网络模型之前要进行归一化处理。供应链客户流失风险分为高、中、低3个档次，是网络的输出数据，在模型处理中可用(0，0，1)表示高风险，(0，1，0)表示中等风险，(1，0，0)表示低风险，表2为经整理并归一化后的供应链客户流失风险样本数据。

2.2 模型构建

供应链客户流失风险的预测是一个寻求复杂问题优化解的过程[8－9]，而 BP神经网络的非线性逼近能力很强，具有易行、高效、并行性强等特点，在预测及分类等应用中都具有较好的表现，因此笔者选用BP神经网络来构建预测模型。BP神经网络在本质上是一种有反馈的前向网络，在算法中采用优化计算中的梯度下降法，利用误差对于权值、阈值的一阶导数信息来指导下一步的权值调整方向，使最终得到的误差最小。为了保证算法的收敛性，学习率η必须小于某一上限，一般取0＜η＜1，而且由于梯度变化值逐渐趋于零，η越接近极小值，算法的收敛就越慢[10]。

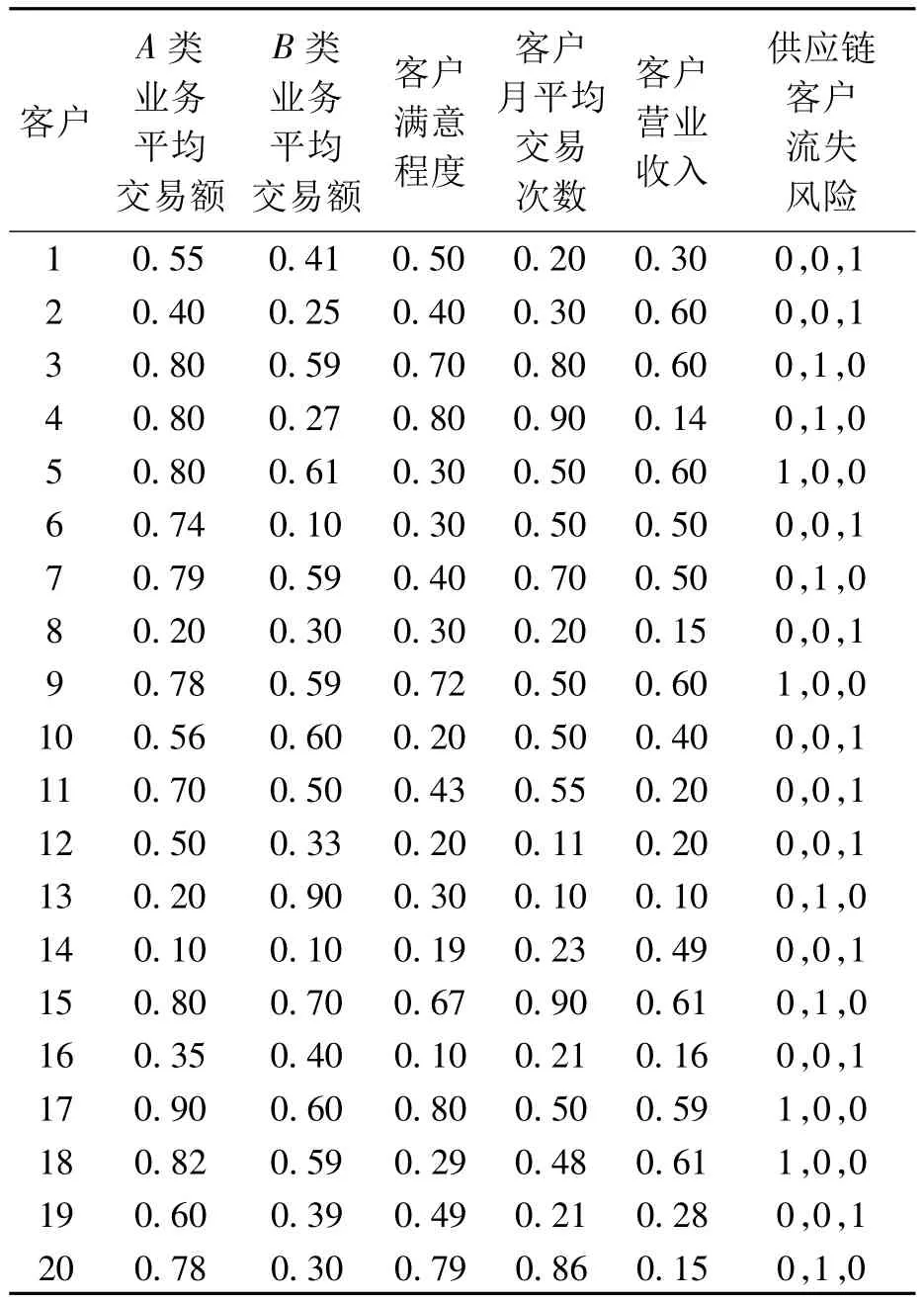
表2 归一化后供应链客户流失风险样本数据

对于具有隐含层的多层前向神经网络，当神经元节点输出函数为可微递减函数，且目标函数取值为时，对于输出单元有，对于输入单元有基于客户历史样本数据，BP神经网络模型构建过程如下[11]:

(1)将BP网络的权重Wjk和阈值初始值θj初始化为区间(0，1)之间的随机数。

(2)随机选取训练的学习样本。笔者选取前13组数据作为训练样本，后7组作为测试样本。

(3)计算隐含层或输出层神经元相对于上一层的输入向量，并选用Sigmoid函数作为传递函数:

(5)调整权值和阈值:

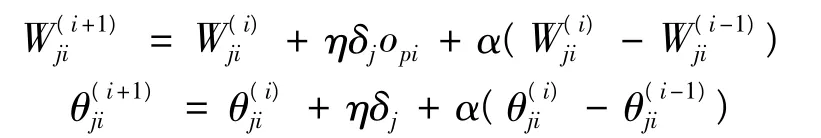
其中，α为学习率，η为梯度搜索步长，η越大，权值修改越剧烈，通常可按如下等式选取:

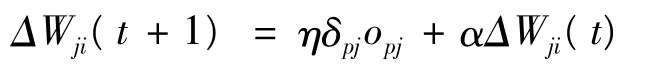
(6)判断目标函数J值是否满足精度要求，当J≤ε(ε为预先设定的一个正极小值)时，则判定网络收敛，学习结束，否则为不收敛，需要返回步骤(3)，直到网络收敛为止。

以上模型构建步骤可用Matlab语言实现，网络的训练误差曲线如图3所示。

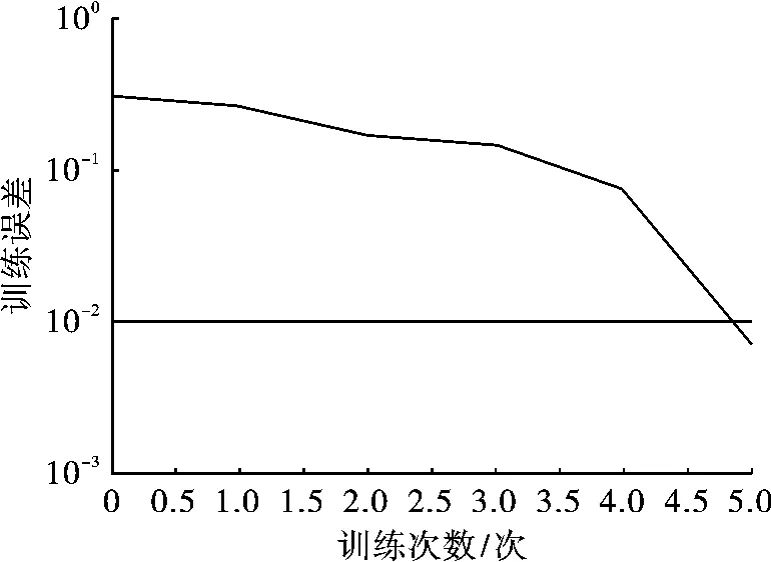
图3 BP神经网络训练结果

可以看出，经过5次训练后，网络性能就达到了目标要求。

输出结果为:

按照欧氏范数理论，7次测试的误差非常小，分别为 0.004 7、0.003 5、0.007 6、0.056 4、0.014 1、0.038 5和0.223 6，各神经元误差曲面与轮廓线如图4所示，另选取3组新的数据测试，表现依然良好，可见网络经训练后完全可以满足供应链客户流失风险预测的需要。

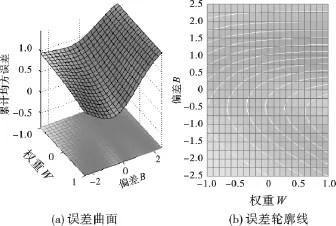
图4 误差曲面和轮廓线

3 结论

BP网络是以监督性学习为基础的前馈神经网络，需要非线性可导函数来进行传导，这种网络连接模型针对具有已知输出的样本集能较为准确地进行预测或分类。笔者通过引入BP人工神经网络，构建了能较准确预测客户流失风险等级的预测模型，可帮助供应链企业采取措施以保留客户。

[1] SARLE W S.Neural networks and statistical models[C]//Proceedings of the Nineteenth Annual SAS Uers Group International Conference.[S.l.]:[s.n.]，1994:1 －13.

[2] 韩力群.人工神经网络理论设计及应用[M].北京:化学工业出版社，2007:56－98.

[3] 田景文，高美娟.人工神经网络算法研究及应用[M].北京:北京理工大学出版社，2006:87－104.

[4] 沈世镒.神经网络系统理论及其应用[M].北京:科学出版社，1998:25－55.

[5] SMITH K A，GUPTA J N D.Neural network in business:techniques and applications for the operations research[J].Computer ＆ Operations Research，2000(27):1023－1044.

[6] 王慧平.基于模糊神经网络的第三方物流项目风险预测[J].武汉理工大学学报:信息与管理工程版，2010，32(5):857 －860.

[7] 元昌安.数据挖掘原理与SPSS Clementine应用宝典[M].北京:电子工业出版社，2009:43－89.

[8] WANG H，GONG C Q，LI Y.Service－mining based on the knowledge and customer databases[C]//Proceedings of 6thIEEE/ACIS ICIS 2007.[S.l.]:[s.n.]，2007:561－568.

[9] WANG H，YUAN H.Service － mining based on customer value analysis[C]//Proceedings of 2007 ICME.[S.l.]:[s.n.]，2007:109 －114.

[10] 蒋宗礼.人工神经网络导论[M].北京:高等教育出版社，2001:101－120.

[11] RYBINSKIO M.Reducing information systems with uncertain attributes[C]//9thInternational Symposium on Foundations of Intelligent Systems.[S.l.]:[s.n.]，1996:366－375.