软时间窗和匹配运输下的供应链配送网络优化

张 霞，张岐山

(福州大学管理学院，福建 福州 350002)

物流配送网络优化问题是物流系统规划的重要课题，它涉及多个要素，包括物流中心选址、客户需求配给和车辆路径优化等，属于NP－hard问题。国内外学者已对物流配送网络优化问题进行了深入细致的研究。朱战国等[1]提出客户供应商匹配运输下的工厂选址问题。该匹配运输模式是对配送网络优化的创新和完善，可以大大减少供应链配送网络中的空车运输次数，从而降低供应链运营总成本。

粒子群优化算法(particle swarm optimization，PSO)由EBERHART和KENNEDY首次提出，是一种基于群体的演化计算技术[2]。该算法具有概念简单、易于编程、收敛速度快和不需要复杂的算子等特点，广泛应用于物流中心选址及车辆路径优化问题中。但是物流中心选址及车辆路径优化问题属于离散组合优化问题，而目前PSO算法一般应用于连续空间优化问题[3]，在离散优化问题上的研究和应用还很少[4]。李宁等[5]提出局部版粒子群算法，用整数编码方式构建了双层粒子模型，分别采用取整和排序规范的方法，通过算例求解取得了比遗传算法更好的效果。肖健梅等[6]设计了实数编码方案，将车辆路径问题转化成准连续优化问题，并采用罚函数法处理约束条件。已有文献大都采用取整方法进行粒子更新，这种方式对于带时间窗的VRP求解质量不高[7]。

笔者针对客户和供应商匹配运输下的供应链配送网络优化问题，建立全新的0－1整数规划模型，采用基于整数编码和交换序的离散粒子群优化算法(DPSO)求解。通过算例将PSO、LPSO和DPSO算法的运行结果进行比较，表明离散粒子群优化算法有较好的性能。

1 优化问题的描述及模型的构建

笔者研究的网络由供应和配送两个阶段构成，优化问题既考虑了工厂选址，又包含了工厂车辆的调度以及客户的分配。运输过程将原材料采购过程和产品配送过程进行匹配运输。假设工厂的自身车队在最大行驶距离内可以进行多次运输，运输过程为整车运输，不考虑订货费用、装卸费用和库存成本。

模型中涉及的参数有:工厂集合(r∈R)，客户集合(i∈I)，供应商集合(j∈J)以及车辆集合(k∈K)。工厂的建设成本为gr，每辆车的固定使用成本为u，每个客户的需求量为qi，每个供应商的供应能力为Qj，每个工厂的生产能力为Mr，车辆最大行驶距离为D，单位产品单位距离的车辆成本系数为 C，客户时间窗为[ai，bi]，Sik为车辆到达客户的时间，p为车辆在客户点处等待损失的单位时间机会成本，e为车辆在要求的时间之后到达客户点的罚值，drijk为车辆行驶的三角回路距离。模型中涉及的决策变量均为0－1整数变量，其中Xr=1为修建工厂r;Zrijk=1为运输车辆k从工厂r到客户i，接着从客户i到供应商j，再从供应商j运送原料回到工厂r;Wrk=1为工厂r派出车辆k。根据以上描述，构建的0－1整数规划模型如下:

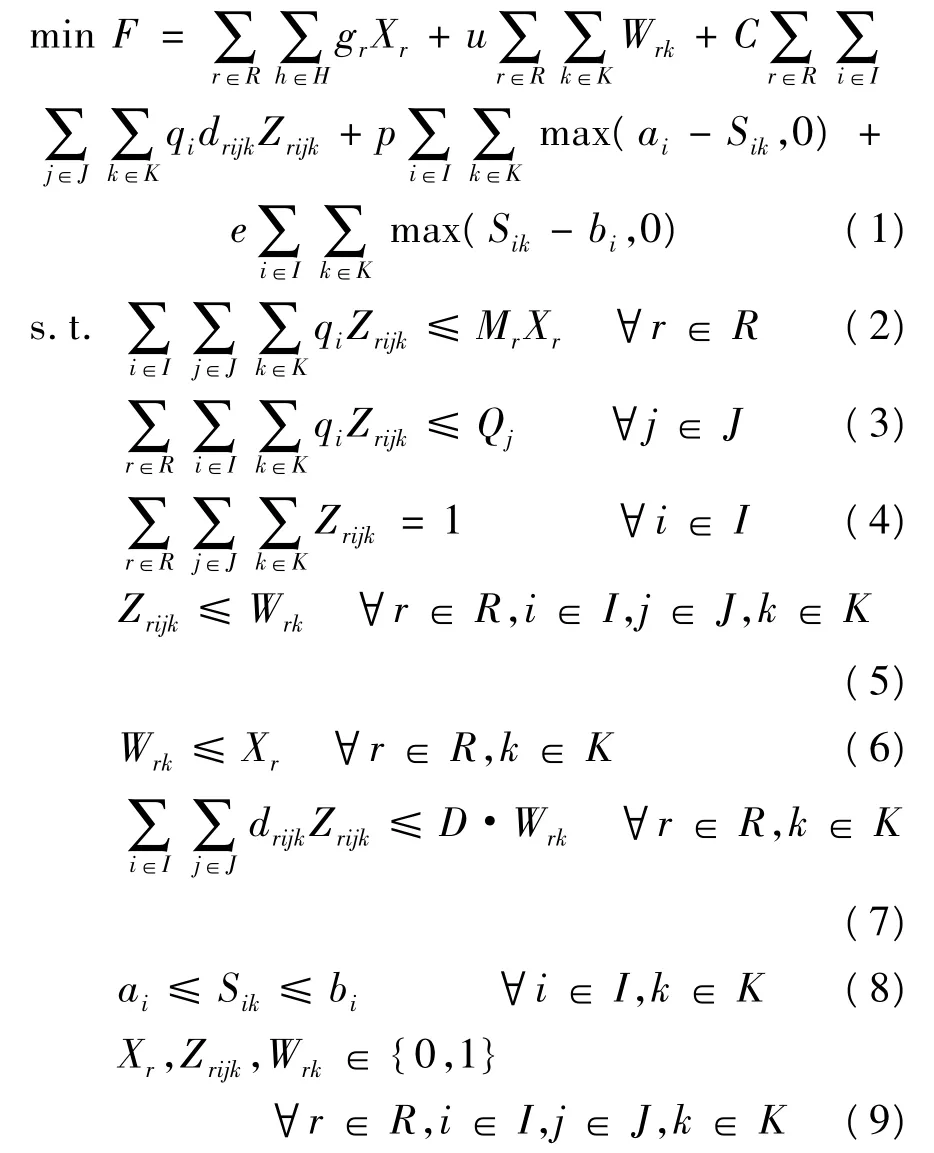
目标函数式(1)表示工厂的选址费用、车辆固定使用成本、运输费用和违反客户时间窗限制的惩罚成本、机会成本之和最小;约束条件式(2)表示每个开建工厂配送的产品总量不超过该工厂的生产能力;约束条件式(3)表示供应商供应的原材料/零部件总量不超过其供应能力;约束条件式(4)表示每个客户的需求被满足;约束条件式(5)表示被工厂选中的车辆才可以用来配送产品和运送原材料;约束条件式(6)表示只有开建的工厂才能派出车辆;约束条件式(7)表示车辆的最大行驶距离限制;约束条件式(8)表示客户的时间窗限制;约束条件式(9)表示决策变量的类型和范围均为0～1整数变量。

2 离散粒子群算法的实现及其求解步骤

2.1 粒子的编码

采用整数编码方法，每个粒子用3层来表示，第一层表示工厂编号，第二层表示供应商编号，第三层表示车辆编号。每一列表示一个运输回路，Xrijk=1(i∈客户集合)表示每个客户的配送方案。每个粒子的位置向量可表示为 Xi(Xi1，Xi2，…，XiD)，其中维数D为客户点数，i∈粒子群，每一维的元素均为整数。例如客户点数为10，工厂数为6，供应商数为8，每个工厂的车辆数为5，则一个粒子的位置编码Xi可表示为:

从以上编码中可以看出被选中的工厂有5个，其中工厂2未被选中;被选中的供应商有6个，其中供应商1和3未被选中;被选中的车辆情况如表1所示。

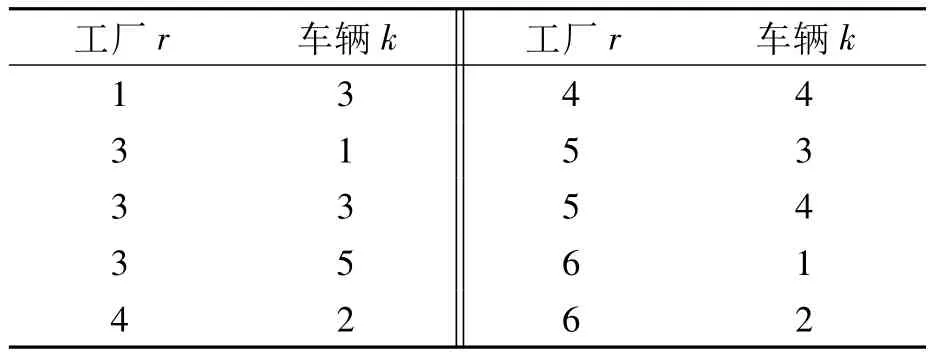
表1 粒子编码对应的工厂车辆分配情况(Zrk=1)

车辆路径表示如下(这里列举两条路径):

Z13=1:工厂1→客户5→供应商6→工厂1(车辆3);

Z31=1:工厂3→客户1→供应商2→工厂3(车辆1)。

上述第一条路径表示车辆从工厂1出发，为客户5配送产品，再到供应商6处运取原材料，最后回到工厂1。其余编码的解码类似。此外，每个粒子的速度向量可表示为 Vi(Vi1，Vi2，…，ViD)，每一维用整数表示。在算法迭代寻优过程中，用速度向量Vi来表示每次迭代中粒子的随机交换序。

2.2 约束条件的处理

笔者采用罚函数法来处理优化模型中的约束条件，取一个较大的正数H作为罚系数，用H乘以违反约束的部分加到目标函数上，如违反工厂生产能力约束的惩罚部分为这样，不可行解将被赋予很大的适应值，在迭代求解过程中，整个微粒群会逐渐收敛于可行解。

2.3 DPSO算法的求解步骤

参照文献[8－10]提出的改进微粒群优化算法，该算法符合组合优化问题的特点，其求解步骤如下:

(1)设定参数w、c1、c2和惩罚系数R。其中，c1、c2为[0，1]之间的可调参数，R 为足够大的正整数。

(2)初始化粒子种群。给每一个粒子赋一个随机的初始解Xid和随机交换序Vid，其维数均等于客户数，均由3层编码组成。第一层的解编码表示工厂编号，每一维随机取1～R之间的整数，相应的交换序编码每一维随机取－(R－1)～(R－1)之间的整数;第二层的解编码表示供应商编号，每一维随机取1～J之间的整数，相应的交换序编码每一维随机取－(J－1)～(J－1)之间的整数;第三层的解编码表示车辆编号，每一维随机取1～K之间的整数，相应的交换序编码每一维随机取－(K－1)～(K－1)之间的整数。其中，R为工厂个数，J为供应商个数，K为车辆数。

(3)用评价函数fitness评价每个粒子的适应值，并将这个适应值作为各粒子的个体最优解Pid，根据个体最优解Pid求出全局最优解Pgd。

(4)根据粒子当前位置Xid计算其下一个位置，即新解:

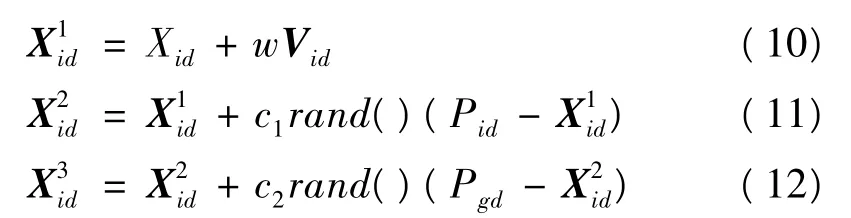
计算Pgd与之间的差根据式(12)计算，以作为新解。

(5)用评价函数fitness评价每个粒子的适应值，并与上一代的Pid和Pgd进行比较，如果较好，则更新 Pid和 Pgd。

(6)如未达到最大迭代次数，则返回步骤(4)。

3 算例分析

算例参照文献[1]，有6个备选工厂，20个客户，10个供应商，每个工厂拥有5辆可选车辆。各参数服从以下均匀分布:工厂的产能服从U(100，500)，供应商的供应能力服从 U(100，400)，客户需求量服从U(10，50)，工厂开建成本服从U(400，600)，供应商、客户、工厂的位置坐标服从U(10，60)。车辆固定使用成本为50万元/年，车辆最大行驶距离为200 km，车辆行驶速度为50 km/h，运输成本系数为0.1，每辆车早上6点从工厂出发，且均为满载运输。以上均匀分布的数据如表2～表4所示。

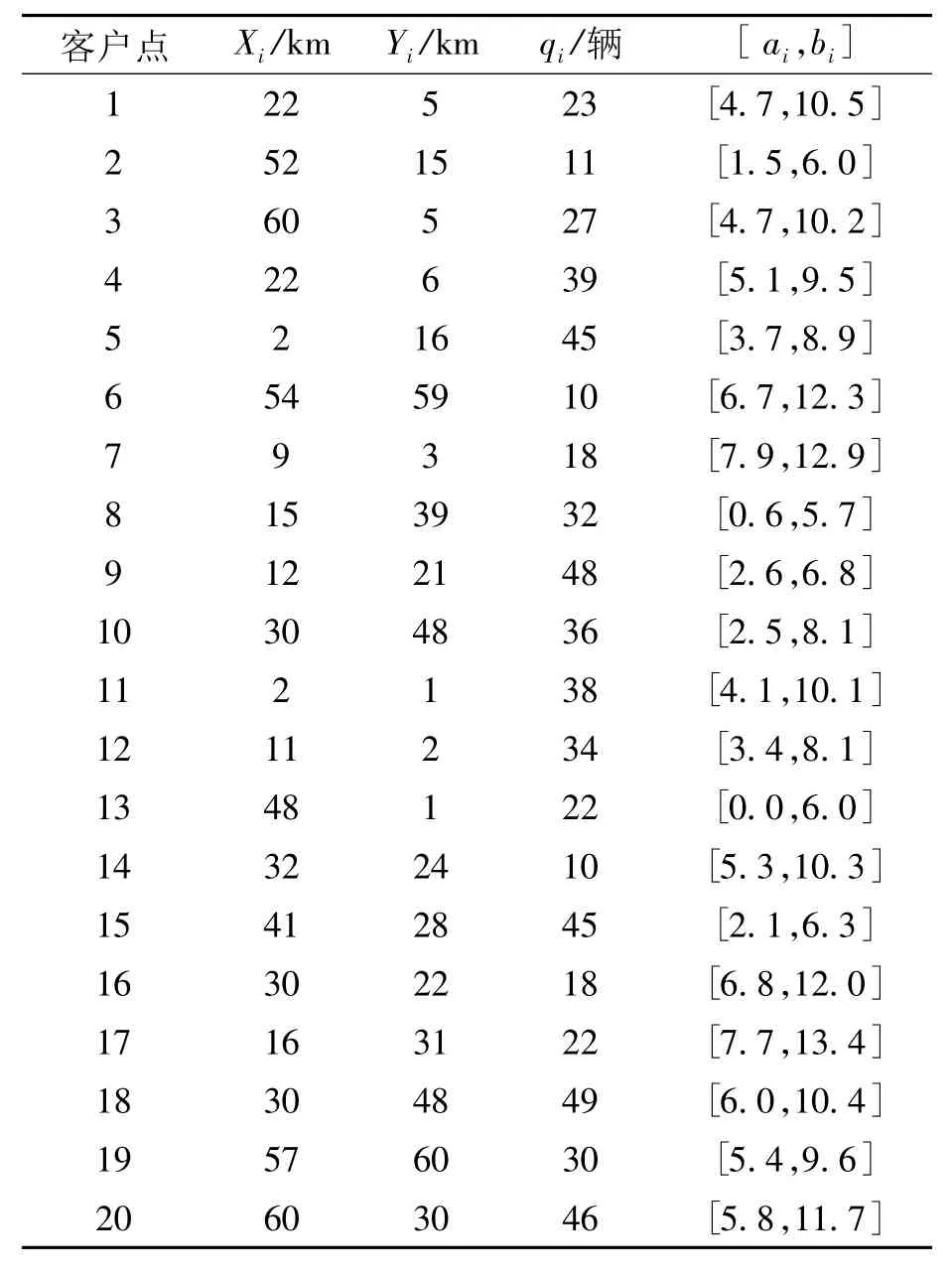
表2 客户的位置坐标、需求量和时间窗上下限

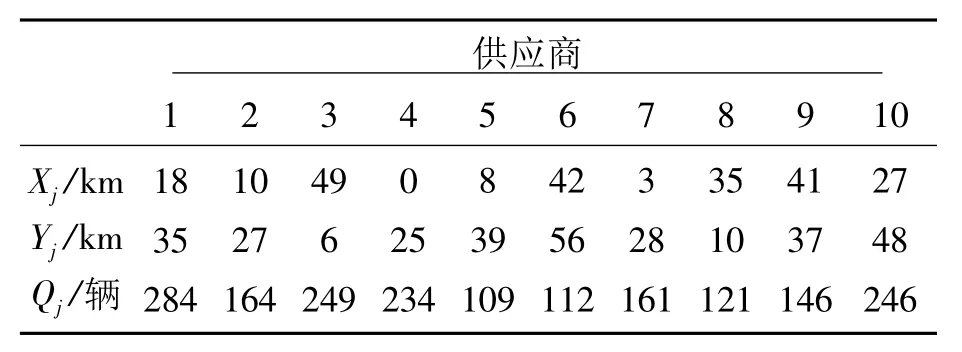
表3 供应商的位置坐标和供应能力

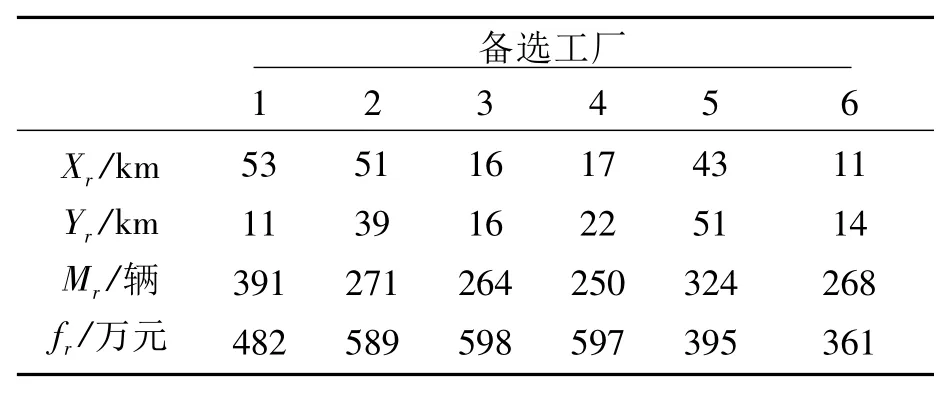
表4 各备选工厂的位置坐标、生产能力(车数)和建设成本

为了便于比较，PSO算法参数设置为:加速因子c1=1，c2=1，惯性权重 w=0.729，进化代数为160，粒子规模为100，违反客户时间窗约束、车辆最大行驶距离约束和车辆容量约束的惩罚系数R=10 000。LPSO算法参数设置为:加速因子c1=1，c2=1，c3=1，相邻子群间重叠粒子数为 3，其他同PSO算法的设置。DPSO算法的参数设置同PSO算法参数的设置。分别将3种算法运行20次后，对其运行结果进行比较分析，如表5所示。

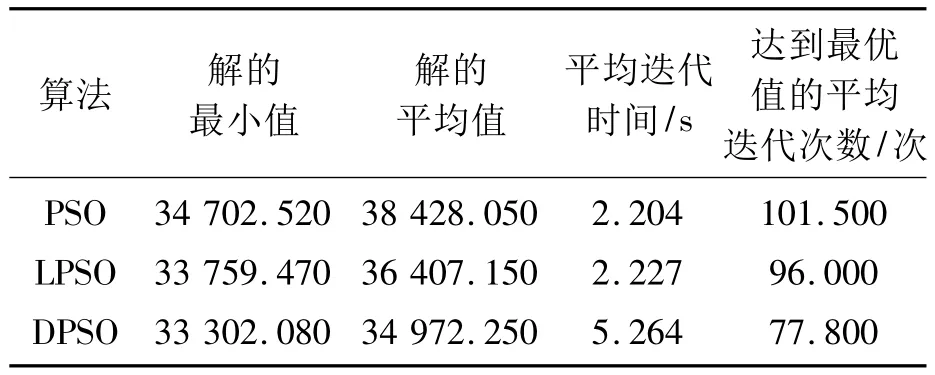
表5 3种算法各自运行20次后结果分析

从表5中可以看出，DPSO算法得到的最优值平均迭代次数和平均最优值都优于其他两种算法。其最优值随迭代次数变化图如图1所示。

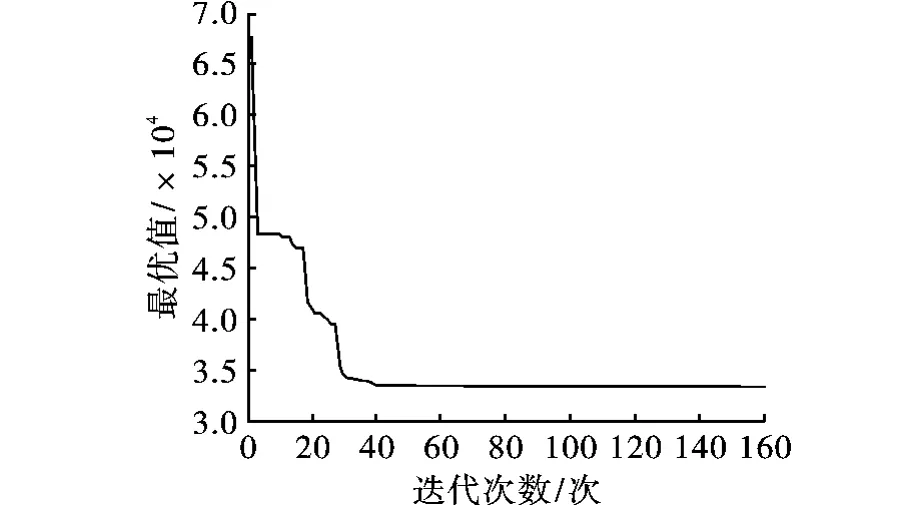
图1 DPSO算法最优值随迭代次数变化图

其中，DPSO算法在第11次运行时的运行结果是最优的，最优值为33 302.080;最优值对应的粒子编码如表6和表7所示。

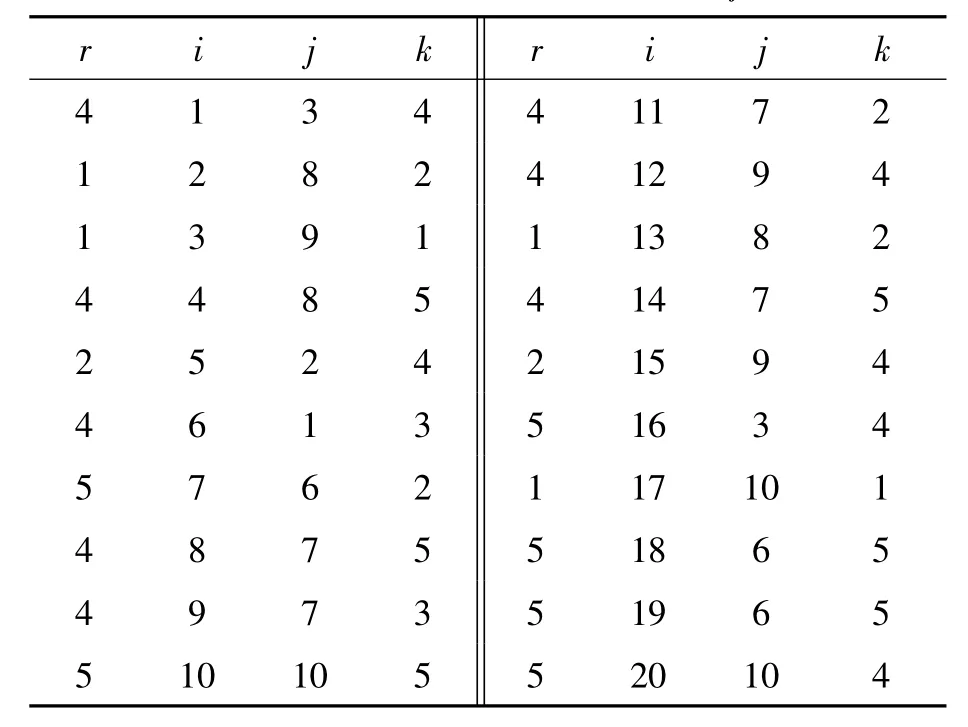
表6 运输车辆分配及匹配情况Xrijk=1

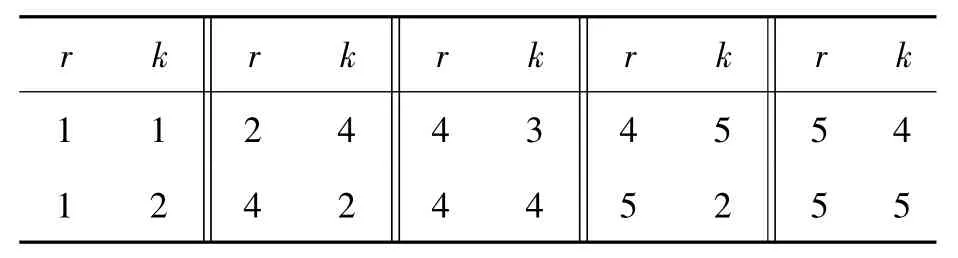
表7 工厂车辆分配情况Zrk=1

4 结论

笔者针对匹配运输下的供应链配送网络优化问题，在模型中加入客户软时间窗约束、车辆行驶距离约束和容量约束，建立全新的0－1整数规划模型，引入基于整数编码和交换序的离散粒子群优化算法(DPSO)进行求解。通过罚函数来处理约束条件，可以有效剔除不可行解。算例分析结果表明，DPSO算法能快速收敛，并能获得较好的优化结果。

[1] 朱战国，孙林岩，吴瀛峰.基于服务距离限制和匹配运输的工厂选址问题[J].运筹与管理，2010，19(2):40－44.

[2] EBERHART R C，KENNEDY J.A new optimizer using particles swarm theory[C]//Proceeding of Sixth International Symposium on Micro Machine and Human Science.Nagoya:[s.n.]，1995:39 －43.

[3] EBERHART R C，SHI Y.Particle swarm optimization:developments，applications and resources[C]//Proc Congress on Evolutionary Computation 2001.Piscataway:IEEE Press，2001:81 －86.

[4] 黄岚，王康平，周春光，等.粒子群优化算法求解旅行商问题[J].吉林大学学报:理学版，2003，41(4):477－480.

[5] 李宁，邹彤，孙德宝.带时间窗车辆路径问题的粒子群算法[J].系统工程理论与实践，2004，24(4):130 －135.

[6] 肖健梅，李军军，王锡淮.求解车辆路径问题的改进微粒群优化算法[J].计算机集成制造系统，2005，11(4):577－581.

[7] 马炫，彭芄，刘庆.求解带时间窗车辆路径问题的改进粒子群算法[J].计算机工程与应用，2009，45(27):200－202.

[8] 肖健梅，李军军，王锡淮.改进微粒群优化算法求解旅行商问题[J].计算机工程与应用，2004(35):50－52.

[9] CLERC M.Discrete particle swarm optimization illustrated by traveling salesman problem[M].Berlin:Springer－Verlag，2004:87 －98.

[10] ZHU Z G，CHU F，SUN L Y.The capacitated plant location problem with customers and suppliers matching[J].Transportation Research Part E，2010(46):469 －480.