基于自适应小生境的改进入侵性杂草优化算法
2012-07-31贾盼龙田学民
贾盼龙, 田学民
(中国石油大学(华东)信息与控制工程学院,山东 青岛266580)
入侵性杂草优化算法(Invasive Weed Optimization,IWO)是由 Mehrabian等[1]在2006年提出了一种新颖的数值优化模型。该算法模仿了杂草入侵的种子空间扩散、生长、繁殖和竞争性消亡的基本过程,具有很强的鲁棒性和自适应性。与遗传算法及其他群智能算法相比,IWO算法简单易于实现,不需要遗传操作算子,能简单而有效地逼近于问题的最优解,是一种强有力的智能优化工具,已被应用到图像聚类[2]、工程约束问题[3]、控制器参数整定[4]、DNA 编码[5]等众多领域之中。
标准IWO算法种群繁殖和优胜略汰的竞争机制都是直接根据个体的适应度来进行的。适应度小的个体产生少量种子或直接被淘汰,很可能会导致附近存在全局最优解的个体被淘汰出局,使算法陷入局部最优,影响到算法的寻优效果。为此,Giri等[6]对空间扩散矩阵做出了改进;Zhang等[7]将交叉操作引入到IWO算法中;Hajimirsadeghi等[8]将IWO算法与粒子群优化算法(Particle Swarm Optimization,PSO)相结合,这些改进方法都在一定程度上增加了IWO算法的种群多样性,使得算法全局收敛性有所提高。
本文将小生境思想引入到IWO算法,提出一种改进的小生境杂草优化算法(Niche Invasive Weed Optimization,NIWO),对种群进行分类竞争繁殖,增加保持种群多样性,提高算法的全局寻优能力,同时采用自适应小生境数来提高算法后期的收敛精度。通过对4个常用标准测试函数的仿真实验,验证了该算法的有效性。
1 标准IWO算法
标准IWO算法[1-3]的执行过程要经历4个过程:初始化种群,生长繁殖,空间分布,竞争性生存。
1.1 初始化种群
初始化量主要有杂草初始个数p和杂草最大个数Q、最大迭代次数it,max、问题维数k、最大和最小可生成种子数Smax和Smin、非线性指数n、区间步长初始值σinit和最终值σfinal以及初始搜索空间X,并生成随机P个初始解。
1.2 生长繁殖
杂草种群中的成员能够产生的种子数是根据该成员的适应值、最大和最小可生成种子数来决定的。
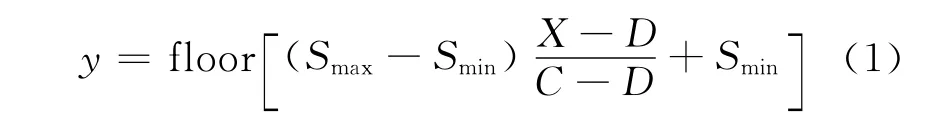
式中,C,D分别为种群最大适应度和最小适应度;x为植株的适应度。图1描述了种子数的确定过程。

图1 种子数计算方法Fig.1 Seed number calculation
1.3 空间扩散
IWO算法种群产生的种子被随机播撒在d维空间中,产生种子的方式是通过将某个解加上某个数值,而该数值的变化区间步长的大小由σ来决定,式中,it为迭代次数;it,max为最大迭代次数;Si为产生的种子在i维上的值;Wi为当前植株在i维上的值。

1.4 竞争性生存
每个植株按照适应度大小进行排序,较优植株产生较多后代,如图1所示。每次繁殖之后,重新按适应度值进行排序繁殖,当族群数目达到最大时,族群数保持固定,适应度差的植株将被剔除。
IWO是一种数值启发性搜索算法,它在函数优化时模仿了杂草克隆的自然行为。该算法的基本步骤如下:① 初始化群体(包括参数的设置和初始解(植株)的生成和评价)。② 生长繁殖,即每个杂草种子生长到开花。对于每个解,根据式(1)确定允许的后代个数。③ 空间扩散,即根据式(2)将产生的种子随机地散布在整个搜索区域,长成新种杂草。④ 重复步骤②和③,直到杂草的最大数。⑤ 竞争排除,即只有较好适应性的前M个杂草个体能生存并产生种子,其他则消亡。⑥ 重复步骤②~⑥,直到最大代数或有更好适应值的杂草个体最接近最优解为止。
2 改进IWO算法
在物种的进化初期,处于不同孤立小生境中的物种之间是不进行竞争而独立生长繁殖的。但随着物种的进化,小生境内个体数量增大,领域也随之扩张,各孤立小生境开始相互融合,使得小生境数逐渐减少。受此自然现象的启发,本文对标准IWO算法加以改进,提出了一种NIWO算法。此方法针对标准IWO 算法[9-13]种群多样性差、易收敛于局部最优的不足,对种群个体进行分类,尽可能地保留一些有用的孤立个体,加强了杂草进化过程中的种群多样性,提高了算法的全局优化能力,同时,采用自适应小生境数策略来提高算法的收敛精度。
2.1 小生境方法的具体实现
小生境方法的基本思想就是物以类聚,反映到IWO算法中就是对种群中所有个体进行分类,使个体在一个特定的生存环境中繁殖竞争。本文分类操作的具体实现如下:
(1)对于每一代的杂草个体按照其适应度进行排序,选定适应度最高的个体B=(b1,b2,…,bk),k∈N作为第1个小生境的中心,并标记此个体;
(2)计算种群中每个个体距离第1个小生境中心B的欧式距离,当欧氏距离小于事先设定好的阈值R(即为小生境半径)时,此个体属于此小生境,并标记此个体;
(3)选择未标记个体中适应度最大的个体作为下一个小生境的中心,计算种群中每个个体距离该小生境中心的欧式距离,当欧氏距离小于事先设定好的阈值R时,该个体属于该小生境,并标记该个体;
(4)重复步骤(3),直到所有个体都被标记,则分类结束。
本文采用如下策略对小生境半径取值

式中,umax,umin与un分别为算法可调参数,用于调节迭代过程中分类的多少;dis为每个个体距离小生境中心的欧氏距离;~R为中间变量。
调节3个可变参数保证小生境半径R随着迭代次数的增大而增大,从而小生境数随之减小,这样就能够提升迭代后期算法的收敛精度。
2.2 NIWO的算法流程
(1)初始化各参数,并随机产生P个初始解;
(2)计算个体适应度,并按适应度进行由优到次的排序;
(3)根据上述小生境实现方法对种群分类;
(4)对于每类杂草个体分别采用图1和式(1)进行生长繁殖和空间扩散;
(5)判断所有解的个数是否大于最大种群数Q,若是,转至步骤(7);若否,则继续;
(6)依次在适应度由优到次的小生镜内筛选一个适应度最优的杂草个体作为胜出个体,当到达最大小生境数时,重新从第一个小生境筛选,直到所有胜出个体的数目等于种群最大个数Q;
(7)判断是否达到最大迭代次数,若是,程序结束;若否,返回步骤(2)。
3 仿真实验
3.1 测试函数
本文选取4个标准测试函数[1]分别对标准IWO和NCIWO进行了算法性能测试。
(1)Shubert函数

此函数有760个局部极小,在(-1.425 13,-0.800 32)处取到全局最小值约为0。
(2)Rosenbrock函数

此函数的全局最优点是(1,1,…,1),最优值为0。
(3)Griewank函数

此函数的全局最优点是(0,0,…,0),最优值为0。

表1 公共参数选值Tab.1 Public parameter value selection
(4)Rastrigin函数

此函数的全局最优点是(0,0,…,0),最优值为0。
上述4个测试函数均为多峰函数,要对其做出满意的搜索结果必须具备较强的全局搜索能力和精确搜索能力。为了更加清楚地说明算法改进的有效性,利用f2,f3,f4进行算法测试时,d分别取10,20。
3.2 参数设定
2种算法中的共同参数取值如表1所示;NIWO算法特有参数取值如表2所示。
3.3 仿真结果
对于每个测试函数,IWO和NIWO算法运行100次后所得性能指标如表3所示。图2所示为2种算法对4个测试函数独立优化100次后所得平均对数收敛曲线。
由表3可见,对于4个标准测试函数,NIWO算法的平均最优值均小于标准IWO算法,而且其方差也显著减小,这说明引入小生境后,IWO算法的全局收敛性有了明显提高,求解结果更加稳定,算法求解效果得到改善。

表2 NIWO算法参数取值Tab.2 Parameters of NIWO algorithm

表3 标准IWO算法和NIWO算法关于测试函数的比较Tab.3 Comparison of the standard IWO and NIWO algorithms for the test function
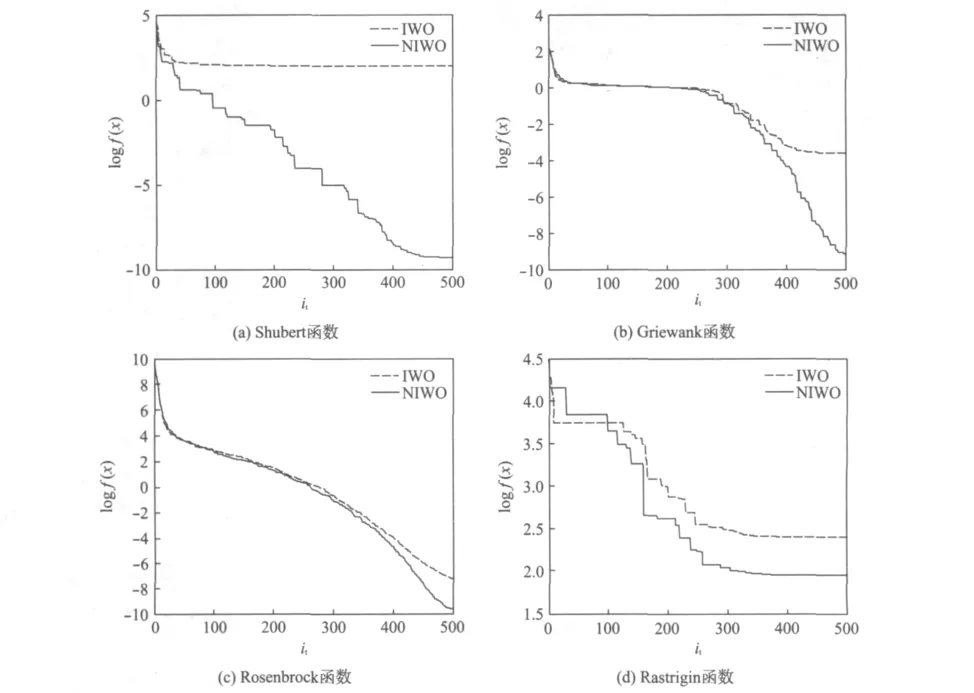
图2 4种测试函数的收敛曲线Fig.2 Convergence curves of 4test functions
由图2可见,在迭代前期,NIWO相对于IWO算法收敛速度没有明显的提高,但由于NIWO算法较IWO算法具有较好的种群多样性,随着迭代次数的增加,其求解结果能更加逼近问题的最优解,求解的精度和稳定性都有所提高。
4 结 语
本文针对IWO算法易陷入局部最优的不足,将小生境思想引入到IWO算法中,对杂草种群个体按照个体之间欧氏距离的大小进行分类繁殖竞争,加强了算法的种群的多样性;同时,采用自适应小生境数策略,随着迭代次数的增加,小生境数逐渐减少,提升了算法后期的收敛精度,加强了算法的全局收敛性能,使得算法在对高维多峰函数进行优化时具有更高的精度和求解稳定性,提高了算法的求解效果。
[1] Mehrabian A R,Lucas C.A novel numerical optimization algorithm inspired from weed colonization[J] .Ecological Informatics,2006,1(4):355-366.
[2] 苏守宝,方 杰,汪继文,等.基于入侵性杂草克隆的图像聚类方法[J] .华南理工大学学报:自然科学版,2008,36(5):95-100,105.
[3] Su Shoubao,Wang Jiwen,Zhang Ling,et al.An invasive weed optimization algorithm for constrained engineering design problems[J] .Journal of University of Science and Technology of China,2009,39(8):885-893.
[4] Chen Zhihua,Wang Shuo,Deng Zhonghua,et al.Tuning of auto-disturbance rejection controller based on the invasive weed optimization[C] ∥2011 Sixth International Conference on Bio-Inspired Computing:Theories and Applications(BIC-TA).Penang:IEEE,2011:314-318.
[5] Zhang Xuncai,Wang Yanfeng,Cui Guangzhao,et al.Application of a novel IWO to the design of encoding sequences for DNA computing[J] .Computers & Mathematics with Applications,2009,57(11-12):2001-2008.
[6] Giri R,Chowdhury A,Ghosh A,et al.A modified invasive weed optimization algorithm for training of feed-forward neural networks[J] .2010IEEE International Conference on Systems Man and Cybernetics(SMC).Istanbul:IEEE,2010:3166-3173
[7] Zhang Xuncai,Niu Ying,Cui Guang Zhao,et al.A modified invasive weed optimization with crossover operation[C] ∥8th World Congress on Intelligent Control and Automation.Jinan:IEEE,China.2010:11-14.
[8] Hajimirsadeghi H,Lucas C.A hybrid IWO/PSO algorithm for fast and global optimization[C] ∥IEEE Congress on Evolutionary Computation.St-Petersburg:IEEE,2009:1964-1971.
[9] Ghosh A,Das W,Chowdhury A,et al.An ecologically inspired direct search method for solving optimal control problems with Bezier parameterization[J] .Engineering Applications of Artificial Intelligence,2011,24(7):1195-1203.
[10] Petrowski A.A clearing procedure as a niching method for genetic algorithms[C] .Proceedings of International Conference on Evolutionary Computation.Nagoya,Japan:IEEE,1996:798-803.
[11] Lin C Y,Wu W H.Niche identification techniques in multimodal genetic search with sharing scheme[J] .Advances in Engineering Software,2002,33(11-12):779-791.
[12] 王俊年,申群太,沈洪远,等.一种改进的小生境微粒群算法[J] .山东大学学报:工学版,2005,35(3):98-102.
[13] 陆 青,梁昌勇,杨善林,等.面向多模态函数优化的自适应小生境遗传算法[J] .模式识别与人工智能,2009,22(1):91-100.
