自动导引车视觉导引路径的识别及精确测量*

喻俊 楼佩煌 钱晓明 武星

(南京航空航天大学机电学院，江苏南京210016)

自动引导车(AGV)是一种广泛应用于工厂自动化生产线和仓储物流的轮式自主移动机器人，是当今柔性制造系统(FMS)和自动仓储系统中的物流运输重要单元［1］．其中视觉导引方式以柔性高、成本低等特点越来越受到国内外研究人员的关注．视觉导引方式是通过在环境中铺设特殊标识线和符号，由视觉系统识别预定义的路径模型，并测量AGV相对导引路径的位置偏差和角度偏差，由控制器按照导引信息完成既定的路径导引任务［2-3］．

在导引路径特征提取和测量算法中，文献［2-3］中采用的灰度图像处理方法极易受到环境光照和路面灰度变化的干扰，而彩色图像包含更多的信息，能够增强AGV对不同环境的适应性［4］．摄像机前倾安装方式［2-4］侧重于预测前方路径信息，无法实时测量当前的路径，只能单向前进，且该方式因视野较大导致路径测量的精度较低．双向型AGV在无碰撞的路径规划上具有较好的柔性，提高了系统的任务调度效率［1，5］．路径测量算法主要包括 Hough变换法［4］和直线拟合法［3］，这两种方法都是针对直线路径的视觉测量方法，对导引路径具有较大的局限性．相比直角拐弯方式［6］，曲线拐弯方式既能保证AGV运行效率，又能提高路径铺设的柔性．视觉导引AGV大多是采用工控机扩展图像采集卡、输入输出工控卡的方式［2-3］，成本高，结构复杂．随着计算机视觉算法和高速数字信号处理器(DSP)的发展，以DSP为核心的嵌入式系统平台，在保证路径测量实时性的同时，降低了视觉导引AGV的成本和功耗［7］．

文中根据双向型视觉导引AGV的模型和目标测量精度，提出了一种基于曲率角估计的路径模型分类算法，将路径分为直线、圆弧转弯和非圆弧转弯3种模型，并分别采用最小均方差法和基于曲率角估计的自适应加权拟合法对这3种模型参数进行回归．最后以TMS320DM642 DSP为嵌入式图像处理单元，实现图像采集、图像预处理、路径识别和测量．

1 视觉系统模型及标定

1．1 视觉系统模型

视觉导引AGV系统模型如图1所示，AGV的驱动系统由两个独立驱动的驱动轮和前后两个万向轮组成．这种结构可以通过调节两个驱动轮的速度和转向，实现直线运动和任意转弯半径的圆弧运动［8］．摄像机位于AGV的中心上方，垂直于地面安装．

图1 自动导引车结构模型Fig．1 Structure model of AGV

与摄像机前倾的安装方式［3，5］相比，在相同的图像分辨率下，图1的方式视野小，但视觉测量的精度相对较高;该AGV能够实现前进、后退双向运动，且运动控制中心在视野内，能够获得即时和未来小范围内的路径信息．但因视野范围较小，弱化了路径预测功能，对视觉测量和运动控制的实时性要求更高．

1．2 摄像机标定及自标定

精确的标定能够消除路径测量的系统误差．平面模型两步法［9］能够精确标定因镜头引起的径向畸变参数及像素相对地面实际物理场景的放大倍数Apix．根据AGV的机械结构特性，当两驱动轮的速度相等、方向相反时，AGV绕两驱动轮轴线的中点原地自转，文中称这个自转中心点为控制中心点，记为C(xc，yc);小车匀速直线运动方向与图像坐标系X轴的夹角为安装角度误差，记为θ，顺时针为正，如图1所示．C(xc，yc)和θ作为计算路径距离偏差和角度偏差的基准，可以在直线和圆弧两种特殊运动模式下实现精确标定［10］．

2 图像预处理

AGV采用彩色CCD摄相机输出逐行倒相(PAL)制式模拟视频信号，经解码器TVP5150行列同步后，输出8位BT．601 YCbCr格式彩色图像至DSP TMS320DM642的VP0口，图像分辨率为720×576［7］．较为常用的彩色图像分割算法是基于 HIS或RGB色彩模型［11］，这两种模型的优点在于能够方便地分割任意颜色特征的目标．如果将YCbCr转换到RGB或者HSI色彩空间，计算过程过于复杂，难以满足系统实时性要求．在YCbCr颜色模型中，Cb、Cr分别为蓝色和红色色度分量，不包含亮度分量，受光照不均匀的影响较小，因此利用Cb、Cr分量能够方便地提取蓝色和红色目标．文中以蓝色导引路径为目标路径，如图2(a)所示为蓝色目标路径在水磨石路面中的彩色图像．对采集图像的Cb分量首先用标定得到的畸变参数校正［9］，然后用5×5线性中值滤波器滤波，降低随机噪声和模糊图像中琐碎的细节．采用自适应全局阈值分割法提取目标路径．阈值分割的二值图像如图2(b)所示，路径为1，背景为0．

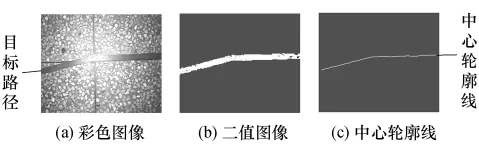
图2 图像预处理结果Fig．2 Result of image pre-processing

提取二值图像中心轮廓线的经典算法是骨架化［11］，该算法计算量大，且在任何微小的孔洞和端点处都会形成骨架分叉的拓扑结构．实际应用中，导引路径可能因局部破损、污染、遮挡和反光等现象造成分割后的二值图像有孔洞或不连通，以致骨架化的数据链表过于复杂．导引路径的分类和测量应提取路径的整体特征，故文中采用四边界轮廓扫描法．即从图像左、右边界向内逐行扫描，遇到1则停止，得到特征向量组 hlj和 hrj(j=1，2，…，576);从图像上、下边界向内逐列扫描，遇到1则停止，得到特征向量组 vti和 vbi(i=1，2，…，720)．对这四个向量组首尾相连组成的离散时间序列特征向量样本，采用主元分析法(PCA)对高维数据降维［12］，获得使方差最大的两组特征向量，将样本降至二维空间．再用支持向量机(SVM)训练［13］，将导引路径模型分为多分支路径和双向导引路径两种．以下仅讨论双向导引路径的模型识别和精确测量．

在双向导引路径下，记导引路径中心轮廓线在图像中的像素点集合为SM，SM是一组离散的轮廓线特征点集，如图2(c)所示．

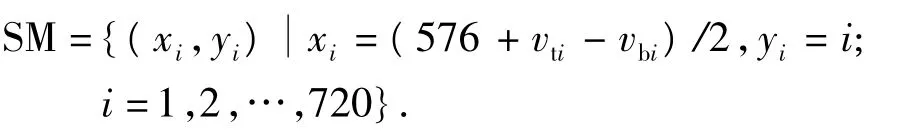
3 双向导引路径模型识别及测量

3．1 基于曲率角估计的路径模型分类

为提高制造系统的柔性，使导引路径能够根据环境的需要简易铺设，双向导引路径在功能上有3种基本的形式:直线路径、圆弧拐弯路径和非圆弧拐弯路径．AGV控制器通过调节两驱动轮的速度差，使其有直线和任意转弯半径的圆弧两种基本的运动轨迹，且其在连续运动过程中，控制中心C(xc，yc)的运动轨迹是光滑的．基于运动预测的LQR最优控制方法［8］，根据当前局部坐标系中的运动模型来预测未来时刻的位姿，将距离偏差和角度偏差同时消除到0．路径实际铺设误差、部分路径残缺或遮挡及图像预处理误差等，都会引起中心轮廓线的观测数据部分无法取得或已取得的数据不真实，使得样本观测数据非同质或残缺或不真实而产生非抽样误差．因此，双向导引路径的识别模型应以全局特征分布为目标对象，在目标最大误差范围内将视野内的路径模型拟合为直线和圆弧路径模型，实时测量其相对控制中心点的距离偏差和相对于小车匀速直线前进方向的角度偏差，并将计算结果传输给运动控制系统．

设在世界坐标系下，容许的最大路径测量误差为σmw，则在图像坐标系中的最大测量误差为

文中提出基于曲率估计的整体识别方法，力求从整体上观测中心轮廓线的首尾间的总曲率角及曲率角的分布特征，对路径模型进行分类，并根据相应的数学模型对中心轮廓点集合进行拟合，使拟合误差小于σmpix．

曲率是曲线上相邻两点的切向量之间的夹角，根据曲率的3种不同定义方式［13］，离散特征点曲率估计有正弦角法、弧微分法和内切圆法．这些方法都是针对矢量工程图或机械零件等局部曲率角变化明显的角点提取，而导引路径在小范围内的曲率角较小，曲线特征不明显，因此，文中提出一种较大观测窗口半径的近似曲率角估计及路径模型识别方法．对中心轮廓点集合SM，取以点(xi，yi)为中心，以观测窗口半径为Rw的观测区域计算近似的曲率角估计．记

式中，lf和lb为观测窗口的两个近似端点．由余弦定理，观测窗口内的曲率角估计为

曲率角估计的均值为

曲率角估计的方差为

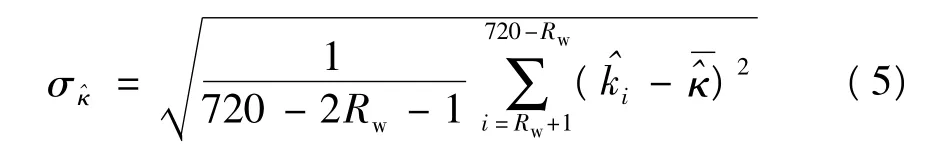
轮廓点首尾间的总曲率角估计为

由于路径不封闭，在首尾两端的观测窗口半径内重复计算的次数较少，总曲率估计有一定偏差，但观测样本越多，偏差越小．

如图3所示为理想状况直线、圆弧、直线圆弧过渡和折线路径对应的曲率角估计．总曲率角估计只与首尾两端的切线方向相关，直线路径的总曲率角估计理想值为0，折线拐弯路径的总曲率角估计理想值为拐弯角度γ．曲率角估计的方差反映了曲率角估计分布的整体波动大小，当中心轮廓线点集存在个别干扰点时，其结果受到的影响不大，直线和圆弧路径模型的理想值为0．因此，根据目标测量精度的要求，对中心轮廓点集曲率角估计的方差和总曲率角设置相应的阈值，即可对路径进行分类．

图3 双向导引路径及其曲率角估计Fig．3 Bidirectional paths and their curvature estimation

3．2 三种精确路径的测量模型

3．2．1 直线路径模型

图4 直线路径模型Fig．4 Model of straight-line path

对中心轮廓点集SM采用最小均方误差法估计参数时，要求观测值yi的偏差加权平方和最小，即

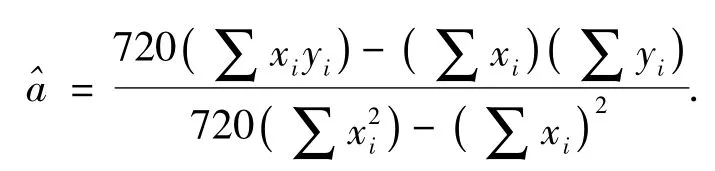
直线路径拟合标准偏差为

当前的距离偏差Ld为小车控制中心C到拟合直线的距离，即

当前的角度偏差α为拟合直线与小车匀速直线前进方向的夹角，

大转弯半径的圆弧路径在图像坐标系中的小段可以近似看作直线路径．为了确定满足σmpix条件下用直线路径替代圆弧路径的转弯半径范围，设在图像坐标系中，转弯半径为R的理想圆弧路径中心轮廓线特征点为由式(8)计算采用直线路径拟合不同转弯半径、圆弧路径的标准方差σpix，如图5所示，圆弧路径的转弯半径越小，标准方差的值越大，σmpix对应的临界转弯半径为RT，RT对应的总曲率角即为κε．由式(6)计算不同转弯半径的理想圆弧路径总曲率角如图6所示．

图5 不同转弯半径直线模型拟合的均方差Fig．5 Mean-variance of straight line fitting for different radius

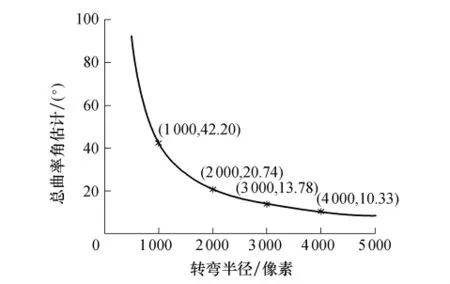
图6 不同转弯半径的总曲率估计Fig．6 Total curvature estimation of different turning radius

3．2．2 圆弧拐弯路径模型

圆是一种非线性模型，为了便于计算，设图像坐标系下圆的方程为

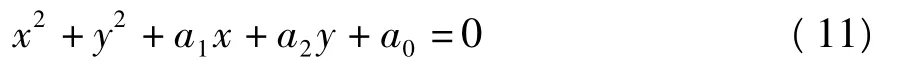
令z=－(x2+y2)，用中心轮廓点集SM估计圆弧路径参数就近似转化为二元线性回归问题:

设ei为SM中像素点(xi，yi)的圆弧拟合误差，根据最小均方误差法，有

图7 圆弧路径模型Fig．7 Model of arc path

其条件是矩阵B的秩r(B)≥3．由于样本数较大，很容易满足这个条件．

圆弧圆心坐标为

转弯半径为

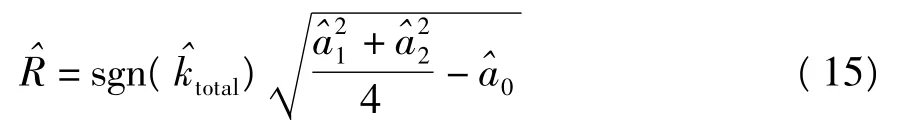
凸形为正，凹形为负．圆弧路径拟合标准偏差为

当前的距离偏差Ld为小车控制中心C到圆弧的距离 CA，即

当前的角度偏差α为过A点的圆弧切线方向与小车匀速直线前进方向的夹角，即

3．2．3 非圆弧拐弯路径模型

非圆弧拐弯路径有总曲率角大且曲率角估计离群的特征，即总曲率角估计＞κ 且．在εκε图像坐标系下的折线转弯模型如图8所示，转弯角度为γ．由于路经在折线顶点处不光滑，AGV要在连续运行的条件下平稳拐弯，宜沿着折线路径的内切圆弧拐弯，从而平滑角度偏差的突变，提高AGV的稳态特性．最小二乘二元线性回归圆弧拟合法对于大的离群观测点不具鲁棒性，由于采用的是平方距离，所以与内切圆弧距离远的那些点，在计算的过程中拥有非常大的权重．为了减轻这些远离点的影响，文中提出一种自适应加权圆弧拟合方法，为每个观测点引入权重因子wi，保留路径两端和远离折线顶点附近观测点的权重，消减靠近折线顶点附近观测点的权重．

图8 折线路径模型Fig．8 Model of broken-line path

定义权重因子如下:

对式(12)采用自适应加权最小均方误差的目标函数为

令 W=diag(w1，w2，…，w720)，则

W是满秩正定对角矩阵，式(21)满足条件:矩阵B的秩r(B)≥3．

加权圆弧拟合的圆心坐标、半径、拟合误差、距离偏差和角度偏差计算方法与圆弧拟合相同，分别为式(14)－(18)．

4 实验结果及分析

南京航空航天大学自主开发的NHV-Ⅱ型视觉导引AGV如图9所示．为了验证图像预处理的鲁棒性，实验条件选择背景复杂的水磨石地面上铺设蓝色路径．NHV-Ⅱ型 AGV的视觉系统由 VS-818HC高清晰工业相机、3．5～8．0 mm 手动变焦镜头VS0358M和TMS320DM642 DSP为核心的嵌入式视频处理平台组成，视频分辨率为720×576，相邻两帧间隔 0．04 s［7］，放大倍数 Apix=2．0656 像素/mm．运动模式下自标定控制中心点C在图像中的坐标为(358．16，280．34)，摄像机相对 AGV 匀速直线运动方向的角度误差θ=－1．53°．在图像坐标系下，拟使路径测量最大误差σmpix=5像素，图6对应的临界转弯半径RT=3900像素，图7对应的总曲率角临界阈值κε=10．59°，则世界坐标系下的最大测量误差σmw=2．42mm．取曲率角估计窗口半径Rw=100像素，由式(5)计算得到圆弧与非圆弧路径判断的曲率角估计均方差离群特征阈值σε=3．22°．

图9 NHV-Ⅱ型视觉导引AGVFig．9 NHV-II vision-based AGV

AGV从直线路径运动到转弯半径为1m的圆弧路径过程中，总曲率角估计、曲率角估计方差、拟合误差和转弯半径随时间(帧数)的变化如图10所示．在前61帧，有＜κ，按照直线模型测量，ε第61帧为临界直线模型帧，其路径拟合的标准偏差最大，但仍控制在目标测量最大误差σmpix内．第62帧为圆弧模型临界帧，之后，转弯半径从－3900像素(逆时针方向)附近逐渐增加到－2000像素，最后趋于稳定．全部过程中，路径拟合误差小于2像素．

图11给出了16°折线拐弯路径的状态．第20帧和第49帧分别为非圆弧拐弯路径模型的临界帧，其间采用自适应加权圆弧拟合算法计算折线路径的近似内切圆弧，其大部分的路径拟合标准偏差都能控制在目标测量最大误差σmpix内，但有几帧超过了σmpix，这是为了平滑路径角度突变，抑制拐点附近的权重造成的，因超出时间短且超出范围不大，对AGV运行影响不大．在开始和最后的直线路径阶段，拟合误差小于2像素．

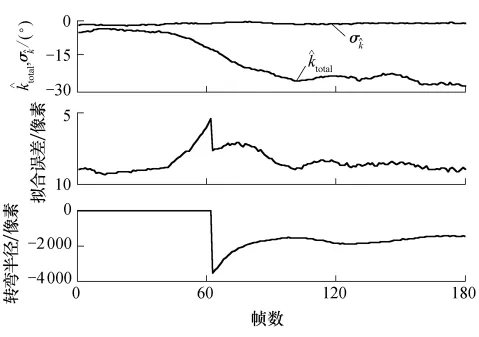
图10 直线到圆弧路径的模型识别及测量Fig．10 Straight line to arc path model recognition and measurement

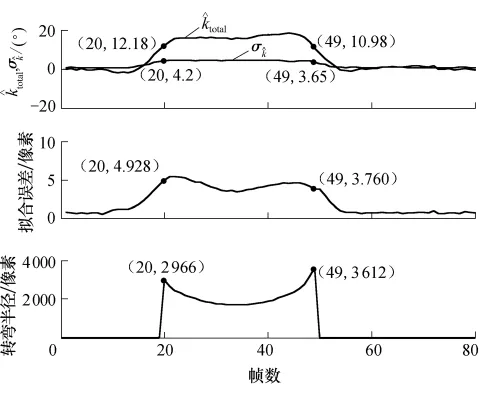
图11 16°折线拐弯路径的模型识别及测量Fig．11 Recognition and measurement of 16°broken line path model

5 结语

文中针对一种将摄像机放置在AGV中心上方垂直于地面安装的双向型AGV结构模型，从3个方面提高了AGV视觉导引路径的测量精度:(1)采用较大分辨率的摄像机，缩小视野的范围，提高测量精度;(2)对因镜头原因引起的图像畸变进行校正，并对AGV采用精确的手眼标定方法，降低测量的系统误差;(3)为了控制视觉系统路径测量的随机误差，采用曲率角估计的方法将路径分为直线、圆弧拐弯和非圆弧拐弯3种模型，通过最小均方差法对这3种路径模型参数进行回归．以TI公司TMS320DM642 DSP为核心搭建嵌入式图像处理平台，实现了图像采集和导引路径的实时测量．试验结果表明该视觉系统的实时性和测量精度达到了目标要求．

［1］ Iris F A．Survey of research in the design and control of automated guided vehicle systems［J］．European Journal of Operational Research，2006，170(3):677-709．

［2］ Ji Shouwen，Li Keqiang，Miao Lixin．Design of a new type of AGV based on computer vision［J］．Chinese Journal of Mechanical Engineering，2004，17(1):97-101．

［3］ 陈无畏，孙海涛，李碧春，等．基于标识线导航的自动导引车跟踪控制［J］．机械工程学报，2006，42(8):164-170．Chen Wu-wei，Sun Hai-tao，Li Bi-chun，et al．Tracking control of automatic guided vehicle based on lane marker navigation［J］．Chinese Journal of Mechanical Engineering，2006，42(8):164-170．

［4］ Zhang Hai-Bo，Yuan Kui，Mei Shu-Qi，et al．Visual navigation of an automated guided vehicle based on path recognition［C］∥Proceedings of International Conference on Machine Learning and Cybernetics．Monterey:IEEE，2004:3877-3881．

［5］ 贺丽娜，楼佩煌，钱晓明，等．基于时间窗的自动导引车无碰撞路径规划［J］．计算机集成制造系统，2010，16(12):2630-2634．

He Li-na，Lou Pei-huang，Qian Xiao-ming，et al．Conflictfree automated guided vehicles routing based on time window ［J］．Computer Integrated Manufacturing Systems，2010，16(12):2630-2634．

［6］ Lee Jin-Woo，Choi Sung-Uk，Lee Chang-Hoon，et al．A study for AGV steering control and identification using vision system ［C］∥Proceedings of IEEE International Symposium on Industrial Electronics．Monterey:IEEE，2001:1575-1578．

［7］ Yu Jun，Lou Pei-huang，Wu Xing．A dual-core real-time embedded system for vision-based automated guided vehicle［C］∥Proceedings of IITA International Conference on Control，Automation and Systems Engineering．Piscataway:IEEE，2009:207-211．

［8］ 武星，楼佩煌．基于运动预测的路径跟踪最优控制研究［J］．控制与决策，2009，24(4):565-569．Wu Xing，Lou Pei-huang．Optimal path tracking control based on motion prediction ［J］．Control and Decision，2009，24(4):565-569．

［9］ Zhang Zhengyou．Flexible camera calibration by viewing a plane from unknown orientations［C］∥Proceedings of the 7th IEEE International Conference on Computer Vision．Kerkyra:IEEE，1999:666-673．

［10］ Chen Huiying，Matsumoto Kohsei，Ota Jun，et al．Selfcalibration of environmental camera for mobile robot navigation［J］．Robotics and Autonomous Systems，2007，55:177-190．

［11］ Sonka M，Hlavac V，Boyle R．Image processing，analysis，and machine vision second edition［M］．2nd ed．London:Chapman ＆ Hall Computing，1999:10-35．

［12］ Zhang Dengsheng，Lu Guojun．Review of shape representation and description techniques［J］．Pattern Recognition，2004，37:1-19．

［13］ Hsu C W，Lin C J．A comparison of methods for multiclass support vector machines［J］．IEEE Transactions on Neural Networks，2002，13(2):415-425．

［14］ Liu Hairon，Latecki Longin Jan，Liu Wenyu．A unified curvature definition for regular，polygonal，and digital planar curves［J］．International Journal of Computer Vision，2008，80:104-124．