零级拟亚纯映射的对数级Borel方向*

陈 湘，吴 佳，刘玉玺

(1．湖北科技学院 数学与统计学院，湖北 咸宁 437100;2．咸宁职业技术学院 中专部，湖北 咸宁 437100)

1 基本定义

为方便我们的讨论，先介绍一些基本定义［1～2］．

定义1 设f是区域D到D＇的同胚

(1)对D内任意矩形{x+iy：a＜x＜b，c＜y＜d}D，函数f(x+iy)对几乎所有的x∈(a，b)是y的绝对连续函数，而对几乎所有的y∈(c，d)，f(x+iy)是x的连续函数．

(2)存在K≥1，使得f(z)=u(x，y)+iv(x，y)在D内几乎处处满足

则称f(z)是D内的单叶K－拟共形映射，若其值域是Riemann球面上的区域，则称f(z)是D内的单叶K－拟亚纯映射．

定义2 设f(z)是平面区域D内的复值连续函数，若对D内一点z0，存在z0的邻域U(D)与一正整数n(依赖于z0)使

是U上的单叶K－拟亚纯映射，则称f(z)在z0点是n叶K－拟亚纯映射，若f在D内每一点都是n叶K－拟亚纯映射，则称f是D内的K－拟亚纯映射．

下面我们给出一些记号的简单解释及S(r，f)的含义，设f是复平面上的K－拟亚纯映射(当K=1时，f(z)就是亚纯函数)．对于任意复数a，记f－a在|z|＜r内的零点总数为n(r，a);若不记零点的重数，则记为珔n(r，a)．相应地，对于角域{|z|＜r}∩{|argz－θ|＜ε}有记号珔n(r，θ，ε，a)．记|z|＜r在映射f(z)=u(x，y)+iv(x，y)下到V上的覆盖曲面为Fr，Fr对V的平均覆盖次数

其中|Fr|与|V|分别表示Fr与V的面积．

定义3 设f(z)是超越K－拟亚纯映射，则

称为f的级，当ρ=0时，称f为零级K－拟亚纯映射;

当0＜ρ＜∞ 时，称f为有限正级K－拟亚纯映射;

当ρ=∞ 时，称f为无穷级K－拟亚纯映射．

定义4 设f(z)是复平面C内的p(0＜p＜∞)级K－拟亚纯映射，如果对任意ε和C内的任何复数a，可能除去两个例外值外，有下列等式

成立，则称从原点出发的半直线argz=θ为f(z)的p级Borel方向，其中n(θ－ε，θ+ε，r，f=a)是f(z)在Ω(θ－ε，θ+ε，r)内零点的个数，重级按其重数计算

2 主要结果

自1997年孙道椿、杨乐［1］的工作发表以来，关于拟亚纯映射的值分布取得了很多重要结果．其中孙道椿、杨乐［1］证明了

定理A设f(z)是平面上的ρ(0＜ρ＜∞)级K－拟亚纯映射，则f(z)至少存在一条ρ级Borel方向．

后来，陈特为、孙道椿(［3］［4］［5］)研究了无限级K－拟亚纯映射的Borel方向的存在性．为了引入他们的结果，先介绍如下结论

定理B［5］设函数B(r)在［a，∞］上连续，且

则存在连续可微函数ρ(r)及U(r)，满足：

(1)ρ(r)单调下降趋于零，ρ＇(r)单调上升．

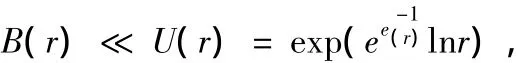
在［5］中，陈特为、孙道椿证明了

定理C设f(z)是Z平面上的无限级拟亚纯映射，U(r)是它的型函数，则f(z)至少有一条关于U(r)的Borel方向，即对任意0＜ε＜δ及任意复数a(至多除去一个零测集)，恒有

其中n(Ω(φ－ε，φ+ε)，r，a)是f(z)－a在角域Ω(φ－ε，φ+ε，r)内的零点的个数，重级按其重数计算．

对于零级K－拟亚纯映射，由于函数增长太慢，研究起来有一定的困难．关于零级K－拟亚纯映射的值分布，虽然有一些结果，但并不完善，比如吴昭君［6］应用零级函数的型函数证明了零级K－拟亚纯映射的Borel方向的存在性．最近，陈天佑［7］引入对数级的概念研究了零级亚纯函数的对数级Borel方向．一个自然的问题是我们能否避开型函数的讨论来研究零级－拟亚纯映射的对数级Borel方向呢?本文主要利用覆盖曲面的几何方法来讨论这一问题，事实上，我们将证明如下定理：

定理1 设f(z)是平面上的满足增长条件

的零级K－拟亚纯映射，则至少存在一条从原点出发的射线L：argz=θ，使得

对任意的复数a及任意的正数ε成立，至多可能除去关于a的两个例外值．

我们称满足定理1条件的射线L：argz=θ为f(z)的对数级Borel方向．

3 相关引理及其定理的证明

为了证明定理1，我们还需要如下引理．

引理1［8］设f是平面上的K－拟亚纯映射;△：|argz|≤a是包含于△0：|argz|≤a0的角域(0＜α＜α0≤2π);a1，a2，…，aq是q个(q＞2)判别复数，则

下面开始证明定理1．

定理1的证明 由于

如若不然，则

又

则

再把△1等分成两块，由(2)知，其中至少存在一块记为 △2．满足

且△1△2，如此一直进行下去，我们得到一个角形域序列{△n}，满足

对于每一个△n都有

由10)，20)，我们可知△n收敛于一条半直线B：argz=θ，下面我们证明半直线B：argz=θ为f(z)一条满足定理1要求的方向．

如若不然．则存在以B为角分线的某角域Ω：{z：|argz－θ|＜ε}以及三个不同的复数a1，a2，a3使得

由于△n→θ0，则对上述ε＞0，存在充分大的n，使得△nΩ．由引理1得

则

结合(3)式有

这与

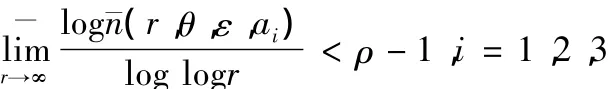
相矛盾．

故假设不成立．这就是说，对于任意复数(至多除去两个例外值)，都有

定理得证．

［1］孙道椿，杨乐．拟亚纯映射的值分布［J］．中国科学(A辑)，1997，27，(2)：132 ～139．

［2］李忠．拟共形映射及其在黎曼曲面论中的应用［M］．北京：科技出版社，1998．

［3］孙道椿．Nevalinna方向的存在性［J］．数学年刊，1986，7A，(2)：212～221．

［4］孙道椿，杨乐．拟亚纯映射的正规族［J］．中国科学(A辑 )，2003，33，(1)：48 ～56．

［5］陈特为，孙道椿．拟亚纯映射的奇异方向［J］．数学物理学报，1999，19，(4)：472 ～478．

［6］吴昭君．零级拟亚纯映射的Borel方向［J］．咸宁学院学报，2003，23，(6)：32 ～33．

［7］陈天佑 ，Common Borel directions of ameromorphic function with zero order and its derivative［J］，Proc．Amer．Math．Soc．2004，132，(4)：1171 ～1175．

［8］宋述刚．拟亚纯映射的 Borel方向［J］．数学杂志，1999，19，(3)：277 ～281．