关于古典概型中一类问题的注解*

2012-07-31成继红

湖北科技学院学报 2012年12期

关键词：样本空间概型蒙特卡洛

华锐，成继红

(1．湖北科技学院数学与统计学院，湖北咸宁 437000;2．新乡学院数学系，河南新乡 453000)

1 问题的提出

在古典概型中，有一类问题，让学生百思不得其解，例题如下：

例：两个质地均匀的硬币，有正反面之分，问：(1)先后投掷两个硬币，两次是不同面的概率是多少?(2)两个硬币一起投出去，不同面的概率是多少?

有学生对上面例题的解答为：

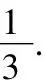
这两个问题的答案似乎都很充分的，是正确的，但是参考答案显示解1是正确的，解2是错误的．解1中，以为两个硬币分别投掷，结果当然有顺序问题，样本空间没有问题，确是古典概型，

问题2是否是古典概型，我们可以用以下两种方法，进行论证．

2 问题的解决

2．1 利用独立性验证

显然，同时投掷两枚硬币，在互不干扰的情形下，我们可以假设他们是相互独立的，根据独立性的定义：若事件A，B 相互独立，则

表2．1 利用独立性验证实验结果

2．2 蒙特卡洛模拟

我们可以用蒙特卡洛法来模拟我们对于此题的2．1中提到的结果，本文分别进行了500，1000，2000次进行了模拟，得到如下结论：

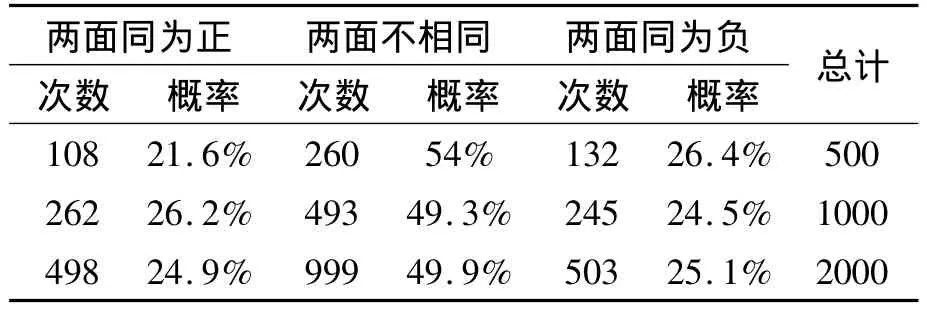
表2．1 利用利用蒙特卡洛法验证实验结果

可见，随着实验次数的不断增加，两面不相同的的概率几乎接近1/2，而其他的样本则接近1/4．也即是若把样本空间看成是Ω={(两面同为正)，(两面同为反)，(两面不相同)}，则每种情况出现的概率是不相同的，不是古典概型．

2．3 直观理解法

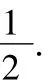
3 问题的总结

本文用了理论推导和实验两种不同的方法都证实，同时抛掷两个质地均匀的硬币，如果把样本空间看成是Ω={(两面同为正)，(两面同为反)，(两面不相同)}时，这并不是一个古典概型．不过，我们通过独立性的证明过程可以清楚的看到，如果把样本空间看成是Ω={(正，反)，(反，反)，(正，反)，(反，正)}，则是古典概型．事实上，只不过是Ω ={(正，反)，(反，反)，(正，反)，(反，正)}的一个不同角度的理解，是 Ω ={(正，正)，(反，反)，(正，反)，(反，正)}的一个拓展，本质上仍然是古典概型．

所以，虽然在字面上看，“两个硬币分别投掷”和“两个硬币一起投掷”存在本质的区别，但实际上，只是问题的“一体两面”．