圆柱孔收缩的弹塑性解及其在隧道工程中的应用

曾英俊，杨敏，孙 庆

（1.同济大学 地下建筑与工程系，上海200092；2.同济大学 岩土及地下工程教育部重点实验室，上海200092；3.中国建筑第三工程局有限公司技术中心，湖北 武汉430064）

圆孔扩张理论经过多年的发展已经成为解决岩土工程领域问题的一种有效方法，并且已经成功应用到土体原位测试和打桩工程中.另一方面孔卸载方法已经被用来预测隧道周围土体和岩体的性质，圆柱孔卸载方法已经用于隧道支护系统的设计中[1].

粘土中的隧道施工速度较快，周围土体性质可认为是不排水的.过去不排水条件下的隧道开挖是基于线弹性－完全塑性的Tresca模型的总应力分析方法[2]，但是该方法不能考虑土体的应力历史、土体的刚度变化以及应变软化和硬化的影响.对于不排水问题可以基于临界状态土力学模型利用有效应力分析方法进行更加准确的计算，Randolph等[3]利用这种方法预测了打入桩周围土体的性质，但是研究中必须要利用有限元方法.Collins等[4]利用临界状态土力学理论发展了孔扩张的解析解法，并已成功应用于正常固结土和超固结土中挤土桩周围土体性质的分析中.Yu等[5]基于临界状态土力学模型给出了柱孔收缩的弹塑性解，并进行了参数分析，但是所得结果不是解析解，需要借助于数值计算，不便于工程应用.

综上所述，用柱孔收缩理论分析隧道开挖的研究相对较少，即便得到的一些有益结论也需要借助有限元或者数值计算，不便于工程应用.本文的主要目的是基于Yu[5]的柱孔收缩的推导方法，引入“破坏区”的概念，用大应变理论得到土体柱孔卸载的弹塑性解析解，并结合土体瞬时沉降的理论得到隧道支护压力和地表最大沉降量之间的关系.

1 问题的定义

根据 Mair和Taylor的建议[6]，隧道开挖问题的分析可简化成如图1所示，图中D为隧道直径.假设隧道的推进如图1a所示，隧道开挖面之后可以有衬砌；隧道开挖施工可以由球孔卸载（图1b）或者柱孔卸载（图1c）模拟.本文采用圆柱孔卸载模拟隧道开挖过程.

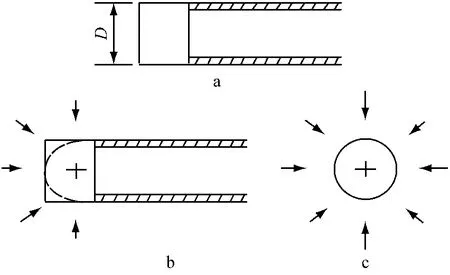
图1 隧道推进简化图Fig.1 Idealization of a tunnel heading

初始状态时将原位应力施加于孔壁，隧道开挖的模拟通过逐渐减小孔压来实现，孔压从原位应力逐渐减小到作用于衬砌上的压力（有衬砌隧道）或减小到0（无衬砌隧道）.

为了分析问题方便，假设土体初始应力状态是各向同性的，并且将圆孔周围土体分为三个区域：弹性区、塑性区及破坏区（图2）.图2中，a0为圆孔的初始半径；rp为塑性区的半径，rl为破坏区半径，在rl＜r＜rp范围内为塑性区，rl以内的范围为破坏区，rp以外的土体仍处于弹性状态；p0为作用在无限远处的静止土压力，p为孔内压力；σr、σθ分别轴向和径向应力.

图2 缩孔问题分析示意图Fig.2 Contraction of cylinder cavity

2 Yu弹塑性解的推导过程简介

首先，简要介绍一下Yu弹塑性解的推导过程，并基于此对其中部分参数重新定义，对其结果进行简化，进而得到柱孔收缩的弹塑性解析解.限于篇幅，仅对其中主要的步骤进行介绍，详细推导过程见文献[5].

2.1 孔卸载的运动方程

由Yu的孔卸载运动方程推导可知：

对于初始半径为r0的土体单元，剪应变为

式中：r、r0分别为土体单元的当前半径和初始半径，a、a0分别为圆孔的当前半径和初始半径.

当孔径为a时剪应变的分布与半径r的关系为

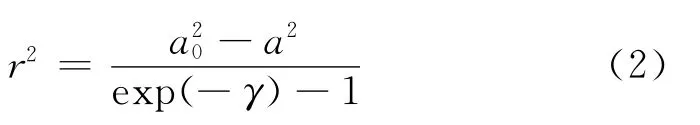
由方程（1）—（2）可知，半径和剪应变增量之间的关系为

2.2 弹性卸载阶段

Yu将p’，p，q分别定义为，，本文根据临界状态土力学的传统定义，将p’，p，q分别定义为平均有效应力、平均总应力和偏应力，具体定义如下：

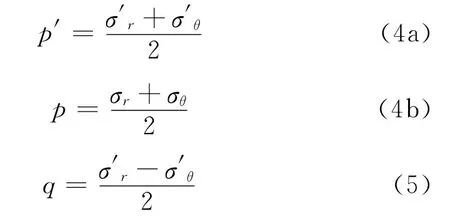
为了简化数学推导，以下推导过程中的应力都除以等效固结压力e进行归一化.对于任一比容ve定义如下：

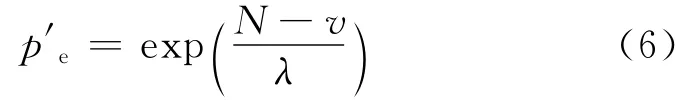
式中：λ为正常固结线的斜率；N为在lnp’—v空间正常固结线上当p’＝1.0时的比容.

归一化之后的有效径向、环向应力分别为

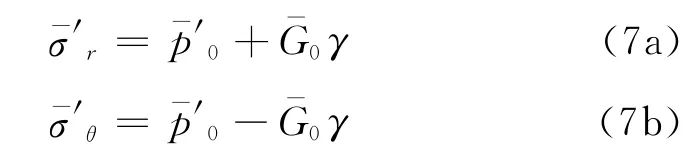
当孔径为a时，由式（2）可得塑性区半径rp为

式中，γ0为初始剪应变.或表示为与剪应变和半径的关系：

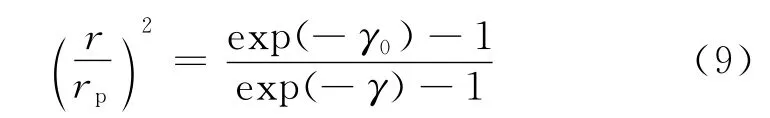
2.3 弹塑性卸载阶段

（1）有效应力分布

屈服条件和塑性流动准则可表示如下：

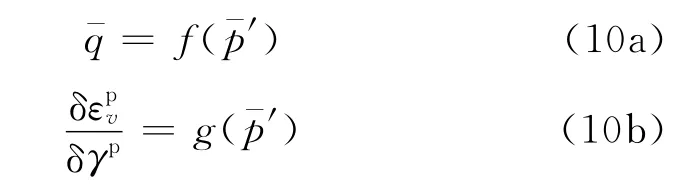
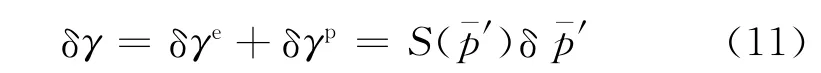
式中：γe为弹性剪应变.

由弹塑性边界开始到塑性区内任一点对式（11）进行积分，可得剪应变γ与归一化的平均有效应力p－′之间的关系为

其中：

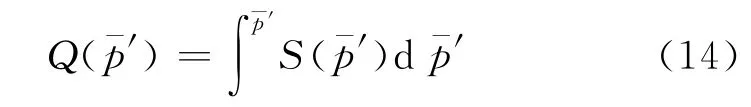
①对于正常固结土

屈服准则和流动法则分别为

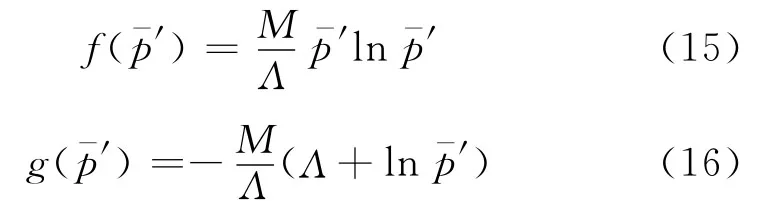
式（15）—（16）中：Λ＝1－κ／λ，κ为回弹曲线的斜率；M是p’—q平面上临界状态线的斜率.模型中的弹性模量为其中：和分别为归一化的体积弹性模量和剪切模量；μ为泊松比；χ为代换系数.

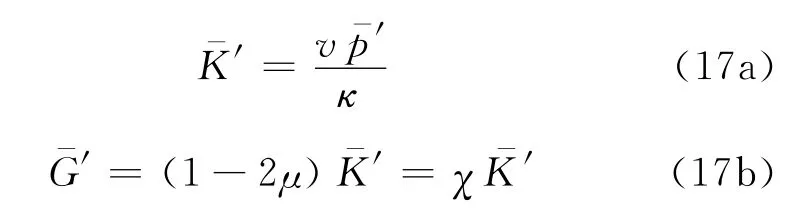
式中，A1＝Mκ／（2Λχv）；A2＝2Λκ／（Mv）.

②对于超固结土屈服准则

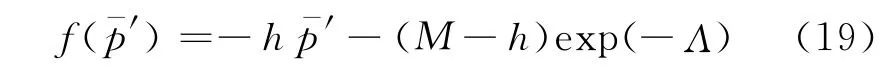
式中：h为 Hvorslev屈服面在p－′－q－空间投影直线的斜率.仍取式（16）作为流动准则.弹性模量取值如下：

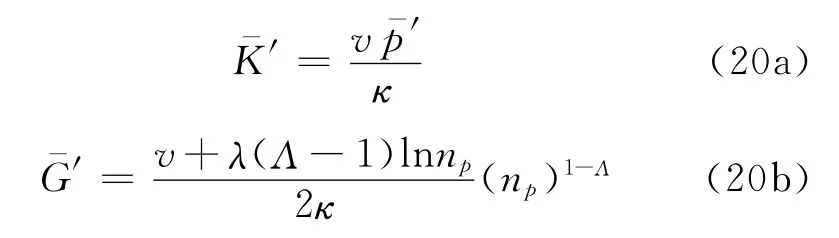
（2）总应力的准静态径向平衡方程：

2.4 塑性区总应力

总应力可通过对式（22）积分得到：

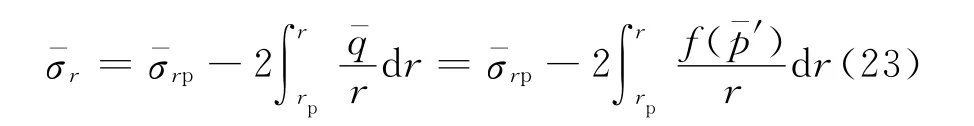
对于正常固结土，由式（3），（12），（13），（15），（16），得到总应力为

可以看出，式（24）得不到解析解，需要借助于数值计算.对于超固结土，结果更为复杂，也得不到解析解，在此不详细列出.

3 公式改进及弹塑性解析解的推导

为了能够得到近似的解析解，这里假设对于大应变情况，孔壁周围的部分土体已经达到破坏，这个区域定义为破坏区，并令rl为破坏区与屈服区交界面的半径，qu为极限偏应力，对于破坏区内的土体有q＝qu，rl可由式（1）和（13）确定：

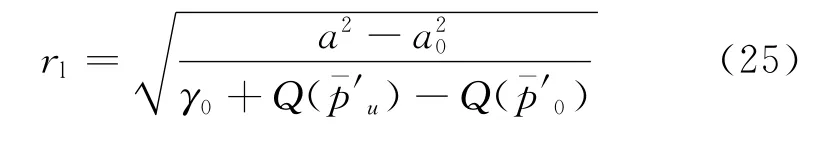
当r＝a时，可得孔壁处的径向应力为

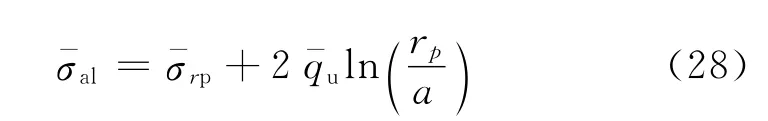
因此，由式（7），（27）和（28）可得孔压为

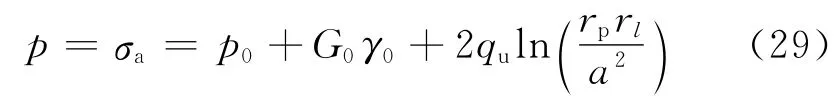
则孔压和隧道内径之间的关系可表示为式（29），或者表示为

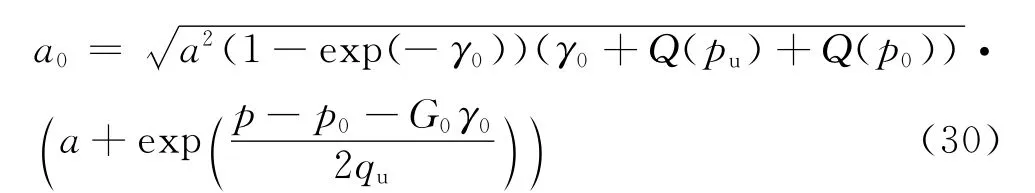
其中，对于隧道开挖工程，a为支护结构的外径，即土体收缩之后的最终半径；a0为土体初始半径.

参照Mair等[7]等提出的地表及地表以下不同深度处最大瞬时沉降值Smax统一的计算表达式：

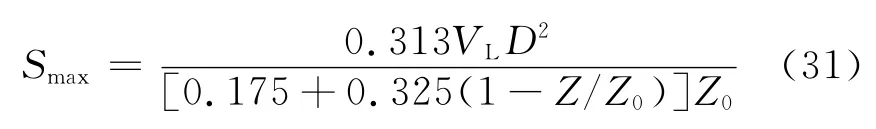
式中：D为隧道直径；Z为计算土层深度；Z0为隧道轴线埋深；VL为地层损失率，定义为

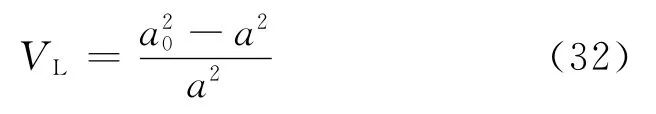
将式（30），（32）代入式（31）并取Z＝0，可得孔壁支护压力与地表最大沉降Smax和地层损失率VL的关系式分别为

对于正常固结土，对式（18）进行积分可得：

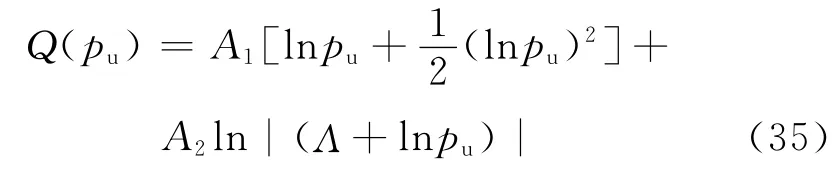
对于超固结土，对式（21）积分可得：

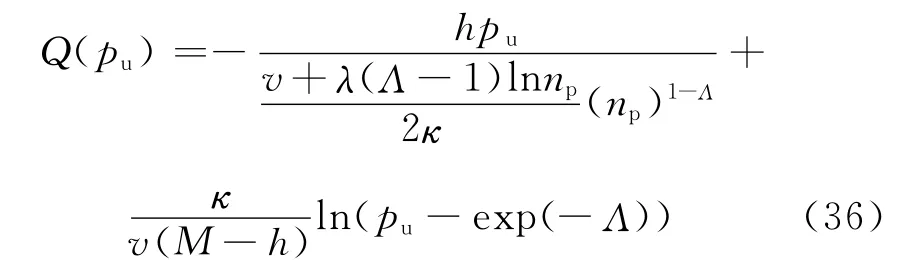
以下算例未做特殊说明时按式（35）正常固结土情况进行取值计算.

4 算例分析

4.1 Grant和Taylor的离心机试验[8]

Grant和Taylor曾利用离心机试验对隧道开挖过程中孔壁支护压力和土体变形之间的关系进行了研究.试验选择高岭土进行模型试验，用逐渐减小孔内气压的方式模拟隧道的开挖过程.试验模型尺寸详见图3（图中尺寸为原型尺寸），主要土体参数详见表1，表中，Γ为lnp′—v平面临界状态线上当p′＝1.0时的比容；Su为不排水抗剪强度；G0为初始剪切模量.

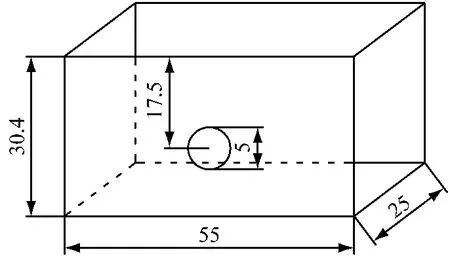
图3 离心机模型试验示意图（单位：m）Fig.3 configuration of centrifuge model test（unit：m）

表1 高岭土主要物理参数Tab.1 Parameters of kaolinite clay

选用表1中的参数，用弹塑性解析解对Grant的离心机试验的地表沉降值进行计算.将地表沉降计算值与试验实测值均绘成曲线，如图4所示.

由图4可以看出，本文方法与试验结果所表现的变形规律相一致，即：随着孔压的减小地表最大沉降值Smax逐渐增大，且增大的速率越来越快.当支护压力大于100kPa时，计算值与试验值吻合得较好，相对差值均小于15 mm；当支护压力小于100 k Pa时计算值与实测值的差值相差相对较大，且差值随压力的减小逐渐增大，但是相对误差几乎不变（｜S计算值－S试验值｜／S计算值约为22%）.

总体来说，计算结果与离心机试验结果在数值上相吻合，所表现的规律相一致，证明用本文方法计算隧道开挖引起的土体变形是合理的.

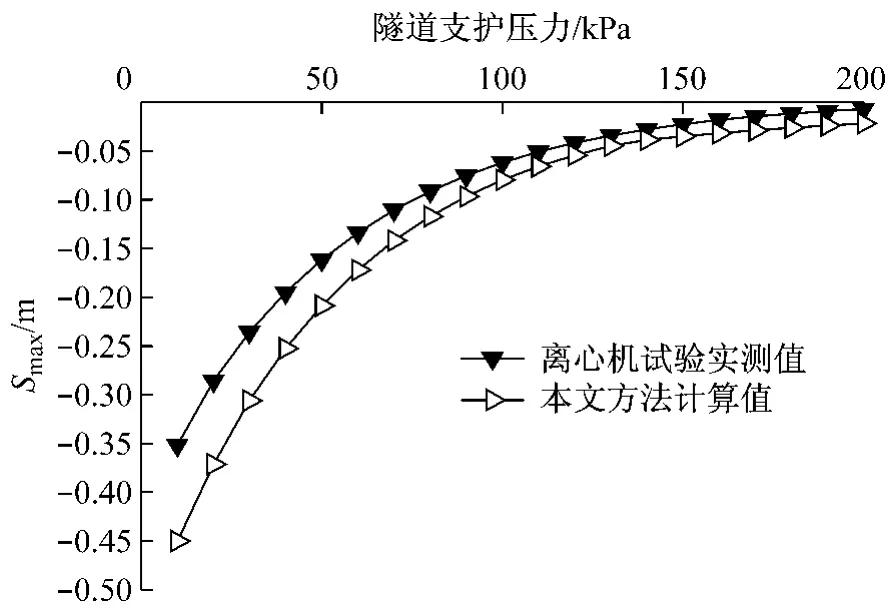
图4 计算结果与离心机试验值对比Fig.4 Comparison of centrifuge tests and thecomputation results

4.2 实际工程实例验证

（1）上海隧道工程实例

上海1964年对直径4.2 m的隧道进行了深层试验[8]，地质条件为饱和含水淤泥质粘土，气压法施工（气压值90 k Pa），隧道轴线埋深15 m.土体参数见表2.

表2 粘土主要物理参数Tab.2 Parameters of clay

该隧道地表最大沉降Smax完工后2年的观测为30 mm（观测2年的土层损失率为3.2%）.已知孔压为90 k Pa，用本文方法计算的地表最大沉降Smax为25 mm土层损失率为3%，和实测结果有一定的误差（｜S计算值－S试验值｜／S计算值约为20%）.因为式（31）为土体变形的短期值，而上述实例中为工后2年的观测结果，且本文方法并未考虑土体工后的固结以及次固结问题，因此计算结果比实测结果偏小是合理的.

上海地铁试验隧道曹溪公园北部段[9]，地层参数与上述工程实例相同，隧道直径为6.41 m，轴线埋深11 m.施工观测时长较短，约为半年，观测地表最大沉降量为75 mm，（土层损失率为2.2%），而Smax计算值为73 mm，Smax计算值略小于实测值（误差约3%）.

（2）英国地铁实例

英国O’Reilly等对Grimsby地区某下水道隧道开挖引起的地表沉降进行了短期沉降和长期沉降的观测[10].隧道直径3 m，共在三个地方进行了沉降监测（包括短期沉降和为期11年的长期沉降），分别标记为A、B、C，埋深分别为8，5.3和6.5 m.本文取气压法施工的B处作为对比实例（气压值41 k Pa）.隧道所处的土层为非常软的海底淤泥，计算参数见表3.

表3 淤泥土主要物理参数Tab.3 Parameters of muddy soil

由于该隧道的沉降观测时间较长，随时间的增长地表最大沉降在不断增大，B监测点地表最大沉降随时间的变化（Smax—t）如图5所示.

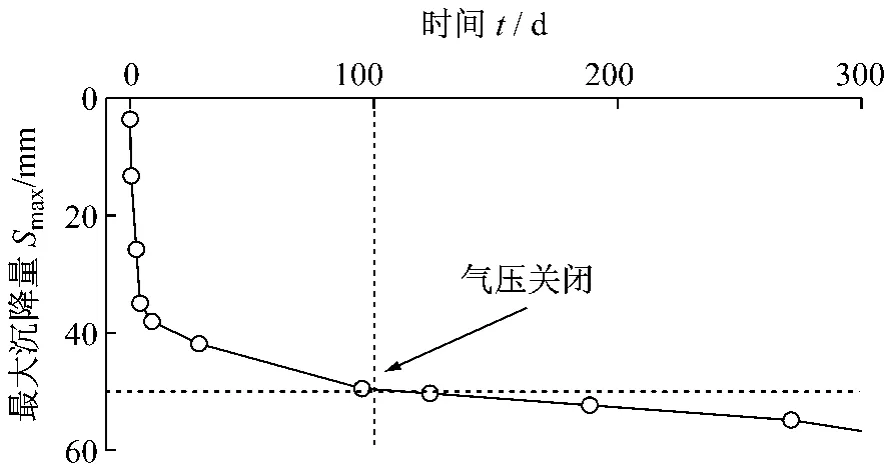
图5 B监测点Smax—t图Fig.5 Smax—t of site B

取“气压关闭”（即隧道完工时t＝100 d）的沉降值为短期沉降值，则由图5可以看出实测短期最大沉降为50 mm.而计算结果为51 mm，二者相差很小（误差为2%）.因此，用本文的圆柱孔收缩弹塑性解计算隧道开挖引起的变形问题是合理的.但是随时间的增长土体固结逐渐完成，横断面的最大沉降值不断增大.本文方法不适于计算隧道开挖引起土体变形的长期影响.

5 结论

本文基于传统的临界状态土力学理论，借鉴Yu圆柱孔收缩弹塑性解的推导过程，给出了圆柱孔收缩问题孔压与孔径变化之间的关系.并把隧道开挖问题简化为圆柱孔收缩问题，得到了隧道支护压力和隧道开挖引起的土体变形之间的关系.

将本文方法的计算结果与Grant的离心机试验结果进行了对比，结果吻合得很好.但是由上海的两个工程实例以及英国的地铁实例可以看出，由于本方法并未考虑软土的固结以及次固结问题，因此计算长期的土体变形存在较大误差.通过与国内外工程实例的对比分析可知，本文的计算方法准确合理，可为隧道开挖引起的短期土体变形分析提供借鉴.

[1] Brown E T， Bray J W， Ladanyi B，et al. Ground responsecurves for rock tunnels[J].Journal of Geotechnical And Geoenvironmental Engineering，1983，109（1）：15.

[2] Lo K Y，Ng R M C，Rowe R K.Predicting settlement due to tunneling in clays [C]／／Tunneling in Soil and Rock，Proceedings of Two Sessions at GEOTECH＇84.Ailanta：American Society of Civil Engineers，1984，48－76.

[3] Randolph M F，Carter J P，Worth C P.Driven piles in clay—the effects of installation and subsequent consolidation[J].Geotechnique，1979，29（4）：361.

[4] Collins I F，Yu H S.Undrained cavity expansions in critical state soils[J]. International Journal for Numerical and Analytical Methods in Geomechanics，1996，20（7）：485.

[5] Yu H S，Rowe R K.Plasticity solutions for soil behaviour around contracting cavities and tunnels[J].International Journal for Numerical and Analytical Methods in Geomechanics，1999（23）：1245.

[6] Mair R J，Taylor R N.Prediction of clay behavior around tunnels using plasticity solutions[C]／／Proceeding Peter Wroth Memorial Symposium，Predictive Soil Mechanics.London：[s.n.]，1993：449－463.

[7] Mair R J，Taylor R N，Bracegirdle A.Subsurface settlement profiles above tunnels in clay[J].Geotechnique，1993，43（2）：315.

[8] Grant R J，Taylor R N.Tunneling－induced ground movements in clay[J].Geotechnical Engineering，2000，143（1）：43.

[9] 刘建航，侯学渊.盾构法隧道[M].北京：中国铁道出版社，1991.354－355.LIU Jianhang，HOU Xueyuan.Shield tunneling method[M].Beijing：Railway Publishing House of China，1991.354－355.

[10] O’Reilly M P，Mair R J，Alderman G H.Long－term settlements over tunnels：an eleven－year study at Grimsby [C]／／Proceedings of Conference Tunnelling.London：Institution of Mining and Metallurgy，1991：55－64.