轻型汽车排放比对试验统计方法探讨

文/卢 彬 陈碧峰 王文炎

我国对汽车排放的检测要求在不断提高，各大汽车生产企业和相关的检测机构都建立了具有国IV排放标准测试能力的轻型汽车排放检测实验室。实验室间的比对试验是确定实验室的检测能力、确保数据质量的标准化活动。

比对试验有多种形式，如：人员比对、设备比对、测试方法比对和实验室间比对等。目前，国内轻型汽车排放比对试验主要聚焦实验室间比对，但对比对试验结果的分析，还没有一套标准模式，各种统计方法都有使用。本文从轻型汽车排放实验室比对试验项目（I型排放试验）着手分析，对各种统计方法在轻型汽车排放比对试验上的运用进行比较，并结合实际案例探讨适合于轻型汽车排放比对使用的规范统计方法。

一、轻型汽车排放实验室比对项目概况

以近期的一次轻型汽油车排放比对试验为例。本次比对试验共有5家国内轻型汽车排放实验室参加，用Lab A～Lab E来表示，试验依据强制性国家标准GB 18352.3－2005《轻型汽车污染物排放限值及测量方法（中国III、IV阶段）》，试验项目为I型试验（常温下冷起动后排气污染物排放试验），每家参比实验室试验次数为3次，用3次试验结果的均值参与实验室间数据的统计比对。

二、比对试验控制条件

轻型汽车排放测试的误差主要来自试验操作人员、环境条件、基准燃油和标准气体、检测设备、检测设备的校准和试验样品等多个方面，故在比对试验前应对试验控制条件进行严格规定，将产生误差的可能性降到最低。由于篇幅原因，不对具体控制条件进行展开。

三、比对试验结果的统计分析

对单个实验室结果自身一致性判定的目的就是及时剔除异常值，为进行多个实验室之间结果统计打下基础。

1.单个实验室结果自身一致性判定方法分析

单个实验室对同样车按要求进行3次I型排放试验，希望取得3次稳定的试验结果（见表1）。如果判定出现异常值，在剔除异常值后需要重新做试验，直至3次试验结果符合判定要求为止。目前常用的单个实验室结果统计判定方法主要有两种：

①按GB 18352.3-2005中的统计量计算判定

计算单个实验室的多次试验结果统计量：

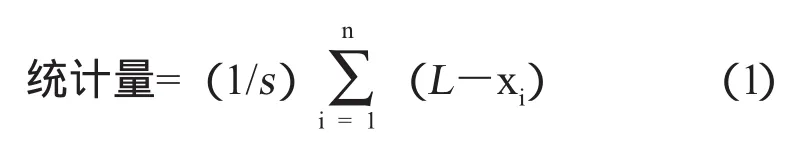
式（1）中：

L：污染物限值的自然对数；

xi：第i次测量的某种污染物测量值的自然对数；

s：生产标准偏差的估计值（测量值取自然对数后）；

n：试验次数。

统计量的通过判定临界值为不小于3.327，具体合格判定参照GB 18352.3－2005中表MA.1的临界值。

统计量反映的是各实验室自身3次数据间的差异以及试验数据与标准限值的偏差，3次结果之间差异越小，平均值离标准限值越远，则统计量越大。

从表2可判定试验结果的一致性为满意。

②按格拉布斯（Grubbs）检验法判断存在异常值

表1 比对试验数据列表 g/km

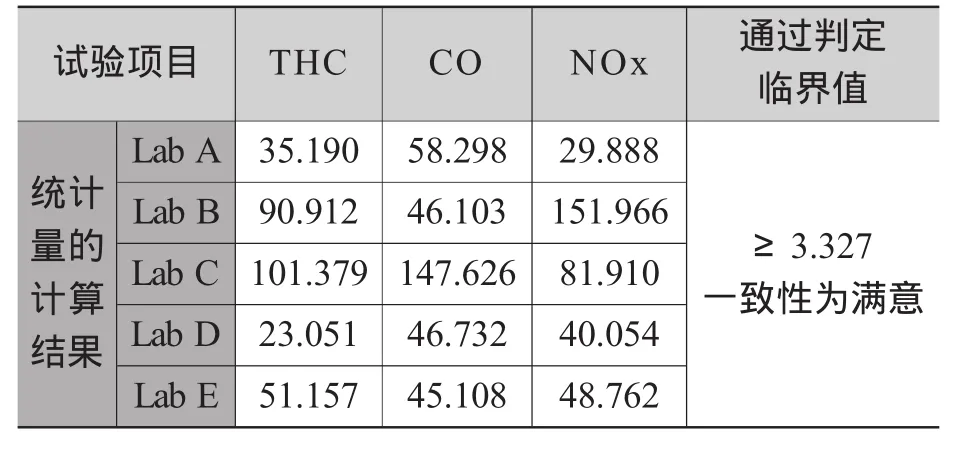
表2 I型试验各参比实验室自身一致性判定（统计量）

a)上侧情形的检验法

对于测量值x1＜x2＜x3，计算统计量：

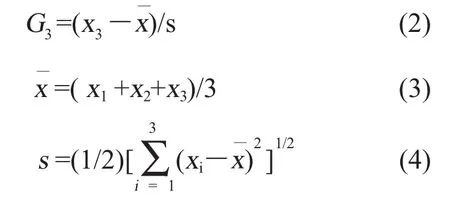
按检出水平α=1%，则G0.99(3)=1.155；当G3＞1.155时，则最大值x3为异常值。

b)下侧情形的检验法

对于测量值x1＜x2＜x3，计算统计量：

按检出水平α=1%，则G0.99(3)=1.155；当G3＞1.155时，则最小值x1为异常值。

从表3可以看出，各参比实验室的CO试验结果无异常值。

为了更好地比较统计量法和格拉布斯法，假设新增LabX的CO试验结果为： （0.20、0.25、1.05）g/km，统计量法的结果是3.275，没有通过一致性判定，而使用格拉布斯法的结果是：上侧为1.153 1和下侧为0.629 0，通过了一致性的判定。可见在排放I型试验单个实验室结果统计判定中，按GB 18352.3－2005中附录M之附件MA规定的统计量计算进行判定较格拉布斯法严格，更适合于实验室自身一致性的判定，及时剔除异常值。其主要原因是统计量法的计算公式中用到了污染物限值，与排放试验的相关度更大，同时随着排放污染物限值的不断加严（降低），统计量的要求也随之变得更高。

2.多个实验室之间结果统计方法分析

实验室间比对的重点就是把多个实验室之间结果进行统计和分析，方法有很多种，如：均值比较方法、标准偏差分析、基于稳健统计的Z比分数法及x¯－R控制图法等。其中最适合轻型汽车排放比对的方法大致可概括为：稳健统计法和经典统计法两大类。

①稳健统计法（基于稳健统计的Z比分数法）

a)用中位值作为公议值

计算过程如下：首先将试验数据从小到大排列X{1}，X{2}，…，X{N}。如果数据数目N是奇数，则中位值med为X{(N+1)/2}；如果数据数目N是偶数，则中位值med为(X{N/2}+X{(N/2)+1})/2。

b)Z比分数的计算方法

各实验室试验结果的Z比分数：

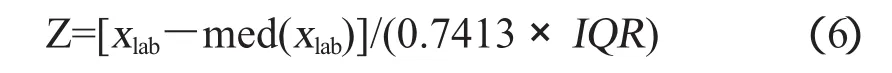
式（6）中：

Z：各实验室的Z比分数；

xlab：各实验室某种排放物试验结果；

med（xlab）：各实验室的某种排放物试验结果的中位值；

IRQ：各实验室某种排放物试验结果的4分位数间距（4分位间距是低4分位数值和高4分位数值的差值。低4分位数值（Q1）是低于结果的1/4处的最近值，高4分位（Q3）是高于结果3/4处的最近值。在大多数情况下，Q1和Q3是通过数据值之间的内插法获得的。IQR=Q3－Q1，标准化IQR=IQR ×0.7413）。

c)实验室Z比分数判定

当|Z|≤2时，试验结果在95%置信区间，试验结果为满意；

当2＜|Z|＜3时，试验结果为可疑结果；

当|Z|≥3时，试验结果离群，为不满意结果。

从计算公式可以看出，在稳健统计法中，中位值只与数据列中间的1个或2个数据有关；低4分位（Q1）和高4分位（Q3）分别只与1个或2个数据有关，因此在稳健统计法中直接决定统计参数的数据不超过6个，特别是数据列两端的数据均不参与计算，对统计参数没有贡献，所以稳健统计法是将极端数据对统计结果的影响降至最低的统计方法，但也容易犯统计学上的第I类错误（弃真）。

虽然稳健统计法是目前检测实验室能力验证中较常采用的方法，但稳健统计方法要求结果数最少为15个以上为宜。因此，建议只有参比实验室数量大于15个以上的排放比对试验才考虑使用基于稳健统计的Z比分数法。

②经典统计法

a)用平均值X¯作为公议值；

b)用标准偏差σ1作为允许离散度；

试验结果的标准偏差σ1按下式计算：

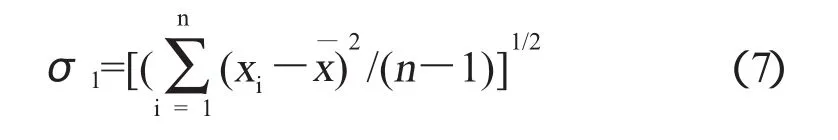
式中：

σ1：多个实验室间试验结果的平均值的样本偏差；

xi：第i个实验室的试验结果的平均值；

x¯：多个实验室间试验结果平均值的平均值；

n：实验室个数。

c)结果判定

所有参比实验室各种污染物的测量值的平均值在标准偏差的±2σ1内（可以根据每次比对实验的要求而变）。

从计算公式可以看出，在经典统计法中，任何一个参比实验室提交的数据都参与计算，都对统计参数做出了贡献，且各参比实验室提交数据的权重相同，因此经典统计法能全面表征数据列的分布特征。同稳健统计方法相比，在比对结果中存在极端值的情况下，经典统计法给出的平均值和标准偏差会受到极端值的影响，因此容易犯统计学上的第II类错误（取伪）。由于经典统计法对统计样本数量的要求不高，并可以方便、快捷地验证试验数据与总体均值的差异，目前被广泛应用于轻型汽车排放比对试验数据统计处理中。

试将本次比对试验的数据用经典统计法进行统计分析（见表4），所有参比实验室间的试验结果标准偏差均控制在±2σ1内，试验结果为满意。

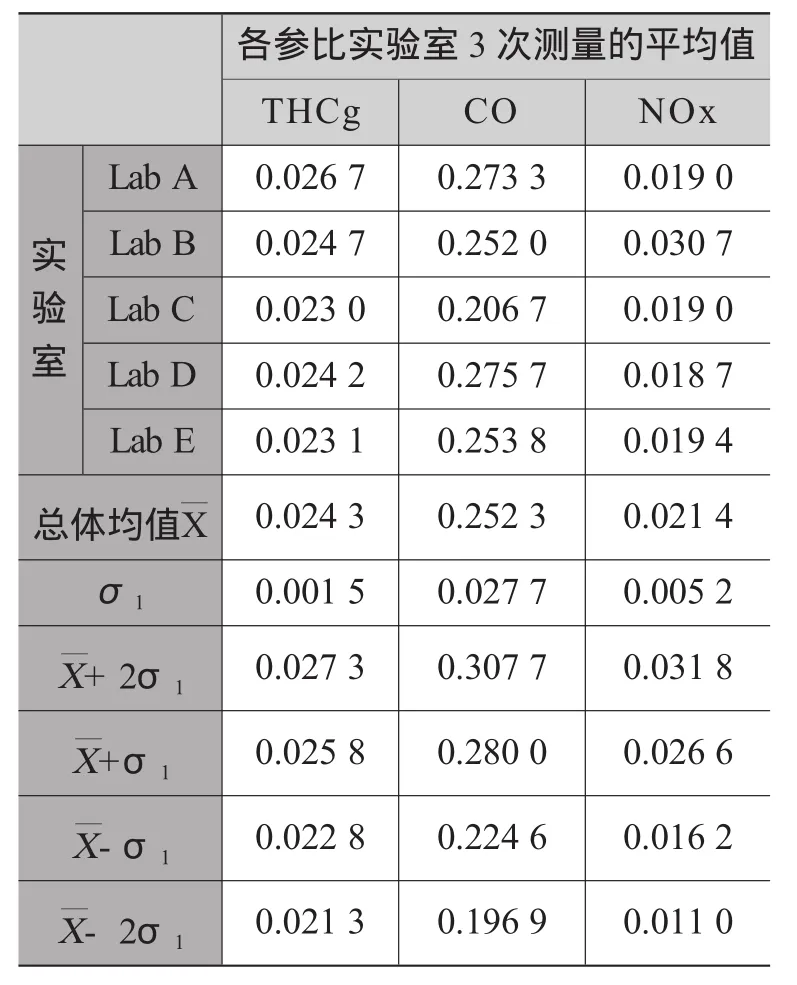
表4 各参比实验室试验结果均值的标准偏差 g/km

同时，为了更好地体现轻型汽车I型排放比对试验的特性，更直接地显示各阶段排放污染物的统计情况，建议增加各参比实验室污染物各阶段测量值均值及其标准偏差示意图（以NOx为例，见图1、图2）。

四、结语

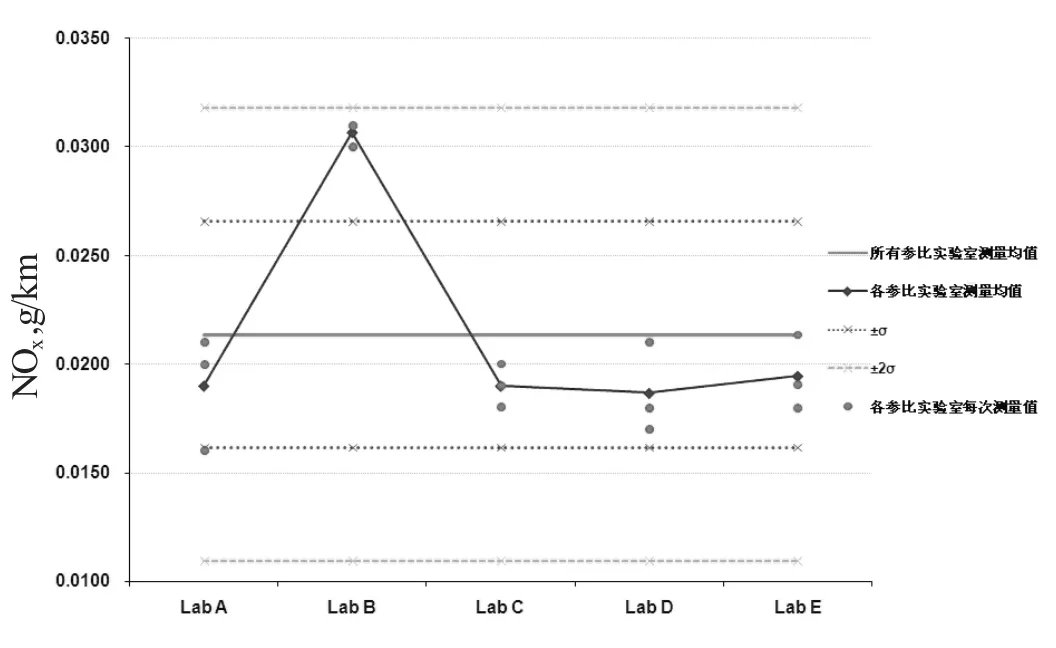
图1 NOx测量值的标准偏差示意图

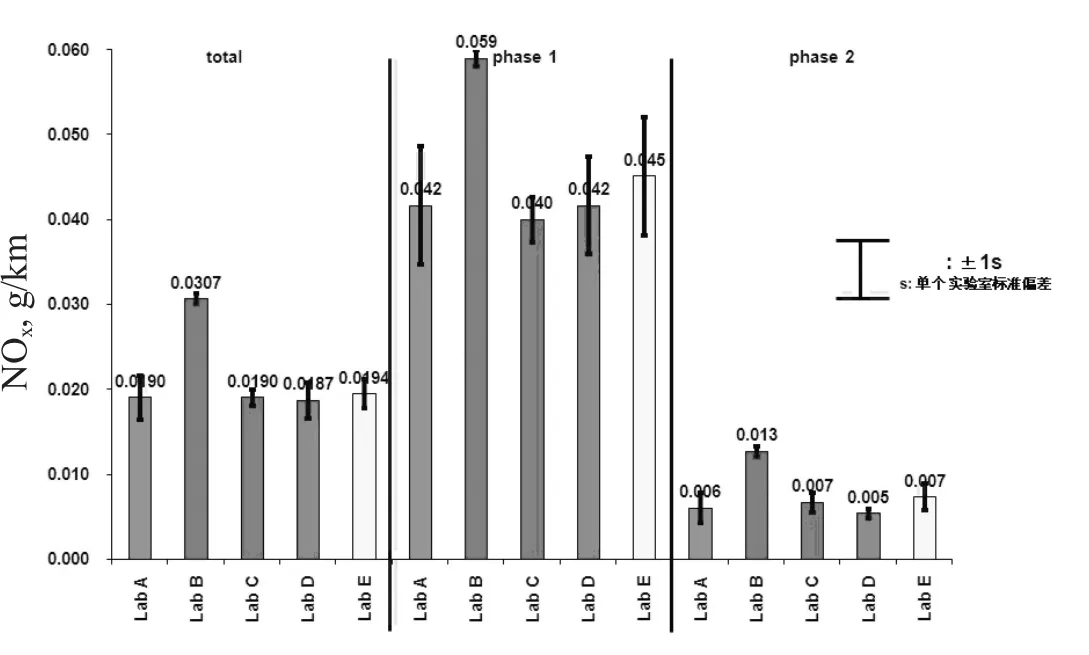
图2 I型试验中各参比实验室NOx各阶段测量值均值及其标准偏差示意图

轻型汽车排放实验室间比对试验有其特殊性和局限性，对试验结果的分析需要选用合适的统计方法，这需要考虑比对数据的分布特征，它在一定程度上与参加比对实验室的数量有关。通过上文对多种统计方法的分析和比较，建议在通常情况下先按GB 18352.3－2005中规定的统计量法进行单个实验室结果自身一致性判定，及时剔除离群值，然后对各实验室测量数据均值采用经典统计法进行统计、分析，并结合各阶段测量值均值及其标准偏差图直观地解析各阶段排放污染物的情况。这应该是目前较适合轻型汽车排放实验室间比对试验的统计方法。

在参比试验室数量较多的情况下（大于15家），可考虑采用稳健统计法给出严格的评价结论。

均值比较方法（由于篇幅原因没有分析）可作为一种辅助的分析手段，对以上两种统计方法进行补充。