索赔相依的非参数近邻估计信度模型

孙 荣

0 引言

信度理论产生于20世纪20年代，至今已有80多年的历史，在非寿险精算理论与实务中具有重要地位，是精算学中最重要的经验保费厘定技巧，是一种经验估费模型。在这类模型中，精算师根据过去的单个风险或者一个保单组合风险的经验数据，调整未来的保险费。从20世纪初到现在，信度理论的研究主要形成了两个不同的分支：(1)建立在频率方法上的有限扰动理论；(2)以贝叶斯理论为基础的最精确一可信度理论。这两种方法都是希望通过已有的历史数据来合理的制定保费。Bühlmann(1967)从Bayes观点出发，建立了无分布信度模型，得到了该模型下的信度保费公式，奠定了信度理论的统计基础。Bühlmann和Straub(1970)从实际运用出发，引进保单索赔的自然权重，得到非齐次与齐次信度估计，并对结构参数提出了相应的估计，使得信度保费能直接运用于实际。这些结果己经成为经典的信度理论。但是，随着精算科学在保险行业中应用的逐步精化、细化，保费价目表变得越来越精细，这些经典信度模型己经不能满足保险产品定价的需要。Bühlmann(1967)建立的信度模型是一种所谓的独立同分布模型，即假设合同之间为相互独立，个体样本索赔为条件独立同分布，且合同之间的风险参数也是独立同分布的。Bühlmann和Straub(1970)虽然将自然权重引入保险合同，但是，假设合同之间相互独立，样本有共同的条件期望，并且条件方差有特殊的结构。很明显这些假定与实际相比过于严格，因为在实际保险业务中，影响索赔的风险是非常复杂的，不仅在保单之间可能存在相依性，而且在时间分量上也可能存在某些趋势。因此，根据实际需要，研究者对经典的Bühlmann信度模型、Bühlmann一Straub模型进行了多方面的拓广，在这些拓展模型中，purearuO和Denuit.M(2002.2003)、FreesE.W 和Wang P(2005)、YeoK.et.etal(2006)、Wen.et(2009)、温利民（2009）等的相依信度模型认为经典的信度理论的风险之间是相互独立的，并且在时间分量上索赔也是条件独立的假设不合实际，在实际中存在许多在时间或风险之间的相依状况。信度保费中同时含有先验信息与样本信息，YoungV.R认为样本分布中的参数容易由样本进行估计，但先验分布本身或先验分布的参数很难估计，她提出用非参数的方法对先验分布进行估计，由此得到半参数信度模型。QianW(2000)提出用核密度估计对先验分布进行估计，并利用非参数方法讨论了信度估计的相合性。Hachemeister(1975)提出了信度回归模型，他在风险参数给定时，根据时间分量上具有某种协变量导致的效应利用普通的回归模型得到了保费估计[1]。本文拟对索赔序列本身存在相依假定下的非参数回归信度模型进行分析，得到在相依条件下经验保费的信度估计。

1 模型设定

k表示每次再抽样的样本容量，是n的函数。令：

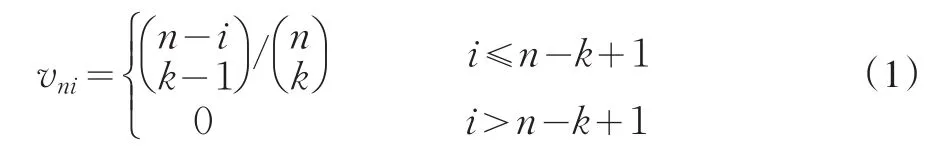
在不重复抽样条件下，vni=P（x的第i个最近邻在一次随机抽样中成为x的第一个最近邻），则回归函数m(X)=E[Y|X]的bagged-最近邻估计为：

设S1,S2…代表各期索赔风险，Pi代表补偿Si的信度保费，H代表一个保费的计算原则，使得对于任何风险，使保险公司能够根据P=H[S]确定保费。此保费可以补偿Si的信度保费。主要的计算原则有：净保费原则、期望值原则、方差原则等。根据Bühlmann的信度理论，在一定条件下，Pn+1=H(Sn+1|S1,S2…Sn)，文献[3]假定S1,S2…是一个平稳的Q阶马尔科夫链，对信度保费提出了非参数核估计的方法，并对估计的渐进性质进行了分析。本文拟对索赔序列提出Q阶平稳马尔科夫链且满足相依（强混合，α-混合）[4]条件假设，对采用净保费原则与期望值原则的信度保费运用非参数的bagged-最近邻估计方法进行分析。强混合（α-混合）条件反映了索赔序列短期的相依性，长期的渐进独立性，这一假定对实际的索赔风险而言是合理的。

净保费原则的信度保费为：

期望值原则的信度保费为：

λ为非负的参数。

令Xi≡(Si,…Si+q-1)T，Yi≡ Si+q，Nn(x)=#{i:‖Xi-x‖＜ δn,1≤i≤n,}，#{i :‖Xi-x ‖ ＜ δn,1≤i≤n,}代表{i:‖Xi-x‖＜δn,1≤i≤n,}中点的个数。δn＞0

则净保费原则的信度保费估计为：

则期望值原则的信度保费估计为：

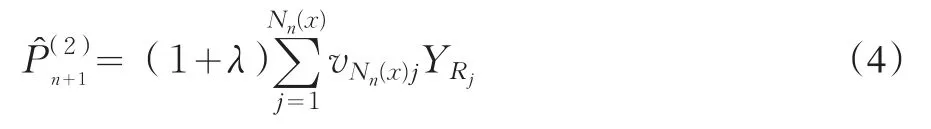
其中，Rj代表{Xi:‖Xi-x ‖ ＜δn,1≤i≤n,}中X的排序，YRj代表与XRj相对应的Yi。

2 主要结论

假定：（1）m满足Lipschitz条件，即∀x∈U(x';δ)|m(x)-m(x')|≤M‖x-x'‖；

（2）文献[5]条件2—5成立；

（3）δn∼n-r，r=1/(2+q)。

若满足上述条件，由文献 [2]、[4]、[5]可以得到：

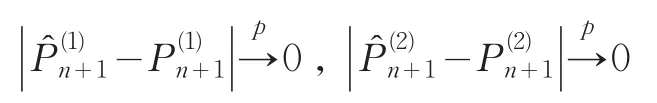
3 实证分析

本文利用丹麦某保险公司1980～1990年火灾超过一百万丹麦克朗（DKM）财产损失索赔数据，以百万丹麦克朗（DKM）为单位，共有2167个索赔记录。相关统计量见表1。

图1 火灾损失资料折线图

表1 火灾财产损失数据统计量

令q=5、n=100、δn=5，分别对1982年、1984年、1986年三年的数据运用公式（2.3）进行拟合对比。拟合结果见表2。

表2 模型拟合误差表

[1] 温利民.风险保费的信度估计及其统计推断[D].上海：华东师范大学，2010.

[2] G.Biau,F.C e,A.Guyader.On the Rate of Convergence of the Bagged Nearest Neighbor Estimate[C].French,INRIA,2009.

[3] Weimin Qian.An Application of Nonparametric Regression Estima⁃tion in Credibility Theory[J].Insurance:Mathematics and Economics,2000,(27).

[4] Richard C.,Bradley.Basic Properties of Strong Mixing Conditions a Survey and Some Open Questions.[J].Probability Surveys,2005,(2).

[5] Truong,Y.K.,Stone,C.J.Nonparametric Function Estimation Involv⁃ing Time Series[J].Annals of Statistics,1992,(20).

[6] Yong,V.R.Premium Principles[Z].Encyclopedia of Actuarial Cience,2004.

[7] B¨uhlmann,P.,Yu,B.Analyzing bagging[J].The Annals of Statistics,2002,30(4).

[8] 谢志刚，韩天雄.风险理论与非寿险精算[M].天津:南开大学出版社,2000.