考虑环向刚度的弹性地基梁法在圆形地下连续墙计算中的应用

陈 红，严宗雪

(广州交通投资集团，广东 广州 510288)

近年来，随着我国交通建设的蓬勃发展，特大跨径的悬索桥得到广泛采用。地下连续墙做为重力式锚碇的重要结构也得到较多运用［1-2］。广州珠江黄埔大桥南汊主桥是广州绕城公路东段上的特大型桥梁，为主跨1108 m的钢箱梁悬索桥，采用重力式锚碇，基坑围护结构为外径73.0 m，壁厚1.2 m的嵌岩圆形地下连续墙。最大基坑开挖深度为30 m，地下连续墙深度为34.00～43.19 m。根据规范，地下连续墙设计采用弹性地基梁法，但圆形地下连续墙采用该方法偏于保守。圆形支护结构是由竖向壁体和水平内衬两组正交的结构杆件形成的较为完整的体系，二者之间的荷载分配与支护结构的直径有直接关系，直径越大，那么支护结构的拱作用就越不明显，结构就越倾向于竖向受力，因此如何在弹性地基梁法中考虑结构的拱作用就是一个突出问题，本文基于壳体弯曲理论，推导适合圆形支护结构的弹性地基梁设计方法，并以工程为例进行计算［3］。

1 圆形支护结构常用计算模型

圆形支护结构承受土压力q作用，即地下连续墙承受竖向q1作用，而圆形内衬则承受水平q2作用，两结构在同一点的变形协调，且有

承受竖向荷载的地下连续墙按弹性地基梁考虑，根据本桥实际情况，可近似按5跨连续梁考虑，如图1(a)所示。圆形内衬可按平面圆环或者壳体考虑，如图1(b)。

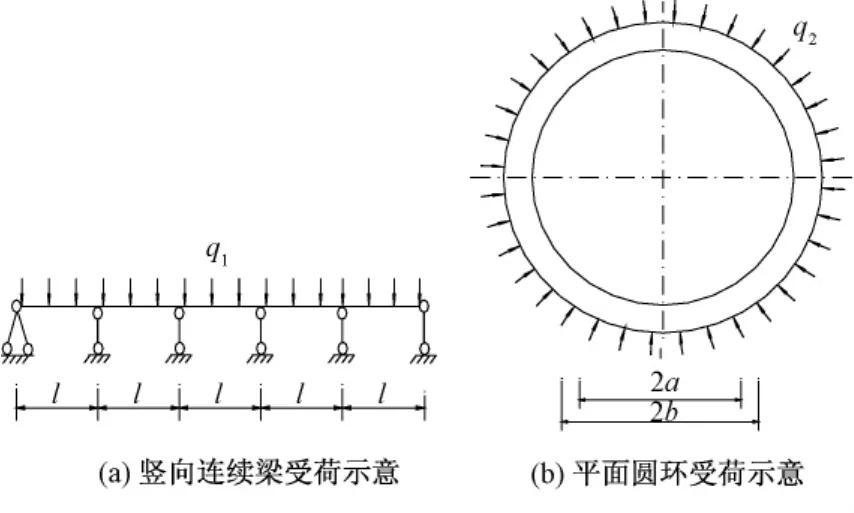
图1 圆形支护结构荷载分配示意

1.1 竖向连续梁模型［3］

跨度为l的5跨连续梁承受外部荷载q1时，跨中挠度为

其中，q1为每跨均布土压力，l为跨径，E1I为连续梁刚度，k为每跨跨中挠度系数。

1.2 平面圆环模型［3］

对于承受外部压力q2的圆环，其径向位移u为

其中，a、b分别为圆环的内外半径，μ为泊松比，r1为中面半径，即r1=(a+b)/2，E2为圆环刚度。

1.3 柱面壳体模型［3］

由于薄壳内只有中面内力，则可假定在整个薄壳的所有截面上都没有弯矩和扭矩，可得到内衬壳体的径向位移 u 为［5］

其中，r2为半径，E3为壳体弹性模量，t为厚度。

2 改进计算方法

2.1 基本假定

①地下墙槽段接头不破坏圆形支护沿环向的连续性;②圆形支护、内衬皆为薄壳结构;③荷载、结构轴对称。

2.2 弯曲方程

根据基本假定，选取坐标 y、z和圆形支护平截面圆心角 φ，如图2。

图2 计算单元脱离体

其中，qn为侧向土压力，qy为土对地下墙侧的竖向支承力;qs为圆形支护扭转的力，荷载轴对称，qs=0;N1为自重，qy对于圆筒支护墙的弯曲问题，N1和qy都可不考虑;N2是地下墙的环向压力。由静力平衡方程Σ y=0、Σ z=0及对s轴的切线取矩之和Σ Ms=0，可得弯曲方程为

2.3 几何方程［3-4］

设中曲面任一点沿 y，s，z的位移用 u，v和 w表示。由轴对称条件可得:v=0，u=u(y)，w=w(y)，且与圆心角φ无关。故沿y向和圆周的应变为

式中，εy和εφ表征中曲面内的拉压应变，R为曲率半径。沿y向的曲率变化υy和沿圆周的曲率变化 υφ分别为

2.4 物理方程［3-4］

在薄壳内沿壳厚度方向的应力σz=0，在距中面z处，有

沿z向，在圆筒壳厚t内积分，可得

式中，Dex

因不考虑 N1和 qy，则有

此即为圆形地下连续墙环向压力的解析解。

2.5 挠曲微分方程［3-4］

综合上述静力、几何、物理方程可得

式(14)可写为

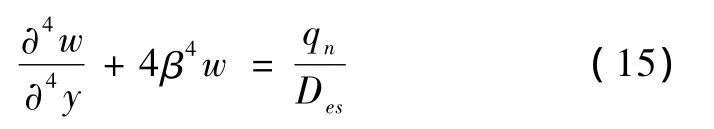
上式与Winkler弹性地基梁方程完全一致。

2.6 模型修正

1)墙身抗弯刚度

圆形支护取单位宽度的y向单元简化为平面问题时，只需将圆形支护壳体的抗弯刚度代替一般直梁的抗弯刚度k1=E1I，其刚度为

2)内衬等效弹簧

内衬不考虑其弯曲效应，直接将其作为弹性支撑处理，其弹簧刚度为

式中，A为横断面面积，k2为弹簧支撑刚度。

3)地基反力

地基反力取值采用m法。

3 算例

3.1 圆形支护结构竖向和水平荷载分配计算

由整个结构的变形协调，可得

当内衬结构按平面圆环模型考虑时，将式(2)和式(3)代入式(18)可得竖向和环向分配的荷载之比为

当内衬结构按圆柱壳体或拱模型考虑时，将式(2)和式(4)代入式(18)可得竖向和环向分配的荷载之比为

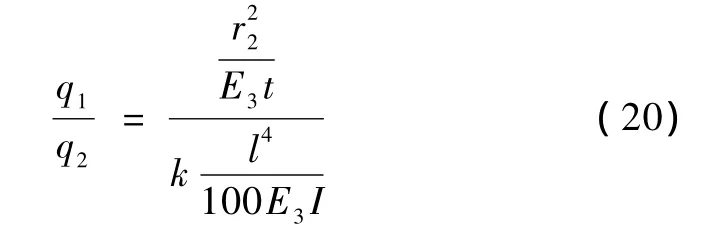
假设地下连续墙和内衬混凝土强度均为C30，则有E1=E2，混凝土泊松比 μ=0.17，圆环外径2b分别取10～90 m，壁厚1.0 m，地下连续墙厚1.2 m，连续梁跨度3.0 m。按式(19)和式(20)计算得到的竖向和水平荷载比，如表1和图3所示。

表1 圆形支护结构竖向和水平荷载分配比

图3 边跨支护结构竖向与环向荷载分配比值与圆环直径关系

3.2 两种计算方法的结构受力计算

为了验证上述计算方法，以南锚工程为例进行验算，基本参数取值列于表2中。考虑到规范推荐的方法不能分析圆柱形支护结构的拱作用，因此还按规范方法采用同样的岩土参数取值进行计算，两种方法结果的对比列于表3中。

对比两种方法的结果可以发现，圆柱形支护结构本身的拱作用十分明显，在计算中应该考虑其有利作用，以减少截面的弯矩和剪力，优化截面设计。

表2 南锚工程计算参数取值

表3 计算结果

4 结论

1)随着圆形支护结构半径的增加，竖向分配的荷载逐渐增加，即圆形结构的拱效应逐渐减小。采用连续梁模型代替弹性地基梁模型来分析地下连续墙结构导致结构变形较小，因而分配的荷载较大。

2)考虑了支护结构的空间作用，即将地下连续墙的拱作用通过等效弹簧来模拟，解决了传统m法应用圆形支护结构的最大难题，工程验算表明地连墙的拱作用明显降低了墙截面的弯矩和剪力，有利于设计的优化，以减小地连墙和内衬厚度，降低钢筋配筋量。

3)本课题的研究不仅解决了广州珠江黄埔大桥锚碇工程中的技术难题，而且对其他类似工程如地铁、民用建筑等方面也提供了可参考的理论依据。

［1］ 徐国平，李健清．圆形地下连续墙在悬索桥锚碇基础中的应用［J］．公路，2004(11):47-51．

［2］ 陈若强．悬索桥锚碇基础地下连续墙施工工艺及质量控制措施［J］．水运工程，2011(4):159-165．

［3］ 广州珠江黄埔大桥建设有限公司．广州珠江黄埔大桥悬索桥锚碇设计与施工技术研究科研项目技术报告［R］．广州:广州珠江黄埔大桥建设有限公司，2008．

［4］ 丁大钧．壳体力学及设计概要［M］．南京:东南大学出版社，1991．

［5］ 上海建筑设计(集团)有限公司．上海市工程建设规范地基基础设计规范［S］．上海:上海市建筑建材市场管理总站，2010．