自适应调整控制参数的差异演化算法

武志峰，黄厚宽

（1.天津职业技术师范大学 信息技术工程学院，天津300222；2.北京交通大学 计算机与信息技术学院，北京100044）

0 引 言

差异演化 （differential evolution，DE）作为一种基于种群之间差异的演化算法，自1995年Storn和Price提出之后，就在数据挖掘、神经网络参数训练、滤波器设计、聚类分析、机器人路径规划等领域得到了广泛的应用［1－9］。

差异演化特别适合于求解非凸、多峰、非线性的函数优化问题。但和其它演化算法一样，差异演化算法控制参数的选择也是一个难题，不同的参数对算法的性能会产生较大的影响。差异演化算法中有3个主要参数：种群规模NP，缩放因子F和交叉因子CR。在原始差异演化算法中，这3个参数是保持不变的。对如何确定算法较好的控制参数人们仍然知之甚少［10］。对给定的具体优化问题，用户依然需要通过手工设置进行多次实验来确定最优的控制参数［11］。为克服手工设置控制参数带来的问题，人们提出了许多差 异 演 化 算 法 的 控 制 参 数 自 适 应 技 术［10，12－13］。文 献［10］提出一种调整控制参数的算法 （FADE算法），利用模糊逻辑动态调整缩放因子F和交叉因子CR。J.Brest等在文献 ［12］中提出一种新的自适应算法 （jDE算法）。该方法对种群中的每个个体都采用各自不同的F和CR生成新个体，同时各F和CR也都随着种群的进化而进化。SaDE算法是文献 ［13］提出的一种自适应算法。它利用种群的学习经历自动选择学习策略并设置合适的控制参数。文献 ［14］提出一种基于PSO学习策略的自适应差异演化算法。在众多的自适应算法中，自适应技术一般主要应用于F和CR这两个参数。这主要是因为相对于种群规模NP，差异演化算法的效率和鲁棒性对缩放因子F和交叉因子CR更敏感［15］。

本文提出一种自适应调整缩放因子F和交叉因子CR的方法，使得参数F和CR能够自动适应不同的优化问题，从而解决手工设置控制参数的不便。同时利用交叉操作生成双子代个体与父代个体竞争形成新一代种群，从而加快了算法的收敛。对标准测试函数的实验结果表明该算法无论在最优解质量和收敛速度上都优于相关算法。

1 DE算法

差异演化是一种利用种群之间的差异推动种群演化的算法。差异演化算法的整体结构与遗传算法类似，但其个体编码采用实数形式与遗传算法的主要区别是其变异操作是基于个体间的差异向量进行的。本质上差异演化是一种基于实数编码的具有保优思想的贪婪遗传算法。

首先，在n维空间里随机产生满足约束条件的NP个染色体 （个体）构成一代种群，其中NP为种群规模。第t代的第i个染色体可表示为Xi（t）＝ （xi1（t），xi2（t），xi3（t），...，xin（t））。然后对种群中的各个个体进行变异生成变异向量hi。在差异演化算法中，常用的几种变异方式如下

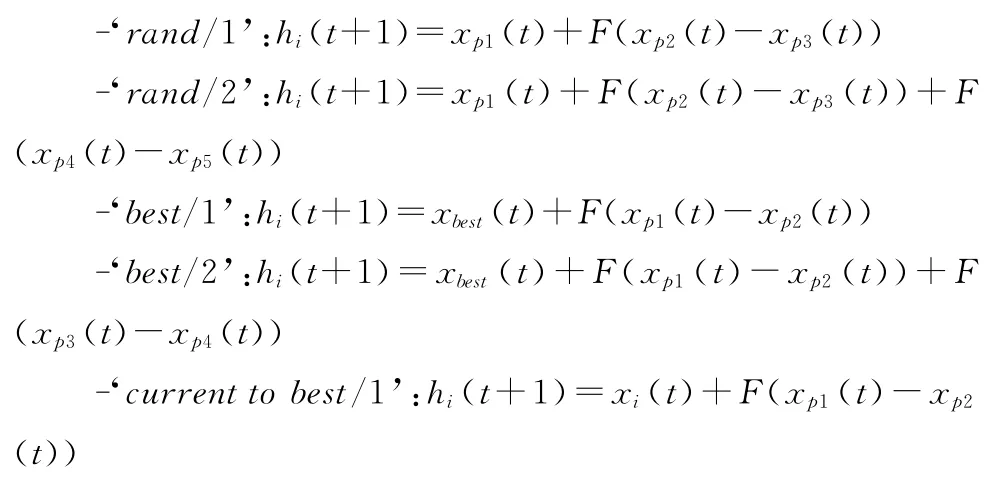
其中xp1，xp2，xp3，xp4，xp5是从种群中随机选择的个体，且 （i≠p1≠p2≠p3≠p4≠p5），F称为缩放因子，取值在［0，2］之间，一般小于1，通常取0.5。

生成变异向量hi后，为增加种群的多样性，变异向量与原目标向量进行交叉操作生成试验向量vi

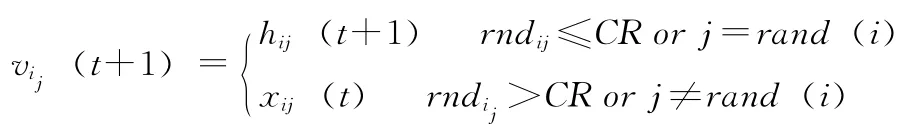
其中rndij是在 ［0，1］之间的随机小数，CR为交叉概率，rand（i）为 ［1，n］之间的随机整数，这种交叉策略可确保xi（t＋1）至少有一分量由xi（t）的相应分量贡献。

最后，计算试验向量的适应度，并与目标向量的适应度进行比较，择优生成下一代成员，如下式所示 （以求最小值为例）

与其它演化算法一样，DE算法的搜索性能取也决于算法全局探索和局部开发能力的平衡，而这在很大程度上依赖于算法的控制参数的选取，如种群规模、缩放因子和交叉因子等。

2 自适应调整控制参数的DE算法 （SelfDE）

2.1 算法原理

对于基本DE算法而言，在种群的整个进化过程中其所有个体对应的缩放因子F和交叉因子CR都是固定不变的。这虽然可以减少算法需要设置的参数，但却在一定程度上影响了算法的效率。因为对不同的优化问题，其对应的缩放因子F和交叉因子CR也可能不同。因而，自动调整缩放因子F和交叉因子CR，以适应不同的优化问题是非常必要的。文献 ［12］提出一种自动调整参数的方法，通过调整概率实现对参数F和CR的自动调整。但在该方法中，并未利用个体适应度作为参数调整的决策依据，调整具有一定的盲目性。我们提出利用个体的适应度作为参数调整的决策依据，并结合一定的调整概率对F和CR进行自适应调整。即针对种群中不同个体采用相互独立的F和CR值，并使其在进化过程中按如下公式自动调整

其中，rnd1，rnd2，rnd3，rnd4是 ［0，1］之间的随机数。f（vi（t）），f（xi（t））分别表示以Fi，t，CRi，t生成的新个体的适应度值和当前个体的适应度值。τ1，τ2表示调整F和CR的概率。由上式可知，对于种群中的一个个体，当用相应的Fi，t和CRi，t生成的新个体的适应度比其当前适应度更差，并且随机数小于给定的调整概率时，重新调整新缩放因子和交叉因子，否则保持原来的F和CR值不变。这种调整策略一方面可以保证当原F和CR的值有效 （即用该参数值生成的新个体适应度优于该个体当前适应度）时，保留原F和CR值到下一代不变；另一方面，如果原F和CR的值无效 （即用该参数生成的新个体适应度劣于该个体当前适应度），则由调整概率决定是否对该个体对应的F和CR进行调整，从而在一定程度上有利于增加种群多样性。对于调整概率的取值，在实验中我们取值为τ1＝τ2＝0.1。

另外，在基本DE算法中，只利用交叉操作生成的一个新个体与父代个体竞争形成的下一代个体。但实际上和遗传算法类似，差异演化的交叉操作可以生成两个 （一对）新个体，每个个体都包含父代个体的部分基因，其交叉操作如下式所示。但在基本DE算法中只用一个新个体参与生成子代，这必然会丢失某些有效信息，从而导致算法陷入局部最优或使其收敛速度变慢。为此，我们提出了双子代竞争模型［16］，即利用交叉操作生成两个新个体vi，ui，然后由这两个新个体与父代个体竞争形成子代个体。同时，为了减少对个体适应度的评估次数，和基本DE算法一样，首先用新个体vi与父代个体竞争，如果vi的适应度值优于父代个体则直接用其作为子代个体，另一个新个体就不必计算；否则再以新个体ui与父代个体竞争

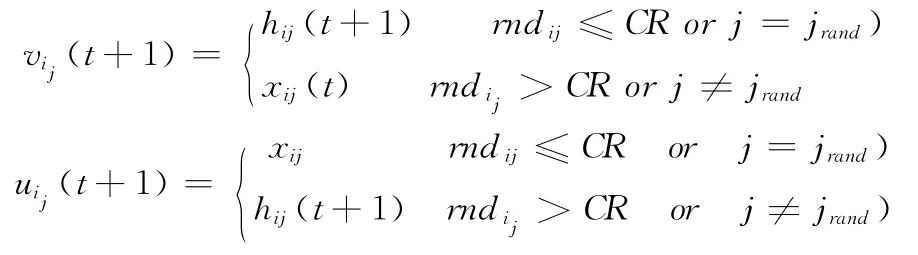
2.2 SelfDE算法

SelfDE算法描述如下：

步骤1 随机初始化第1代种群；

步骤2 对种群中的每个个体i执行如下操作：

（1）随机选择3个互不相同的个体；

（2）对个体i执行 ‘rand/1’型变异操作生成变异向量hi；

（3）利用两子代生成策略形成两个试验向量vi，ui；

（4）对试验向量vi，ui与目标向量xi执行选择操作生成下一代个体；

（5）按2.1节给出的公式动态调整个体i对应的F和CR值；

步骤3 若不满足结束条件，转步骤2；

步骤4 输出结果。

3 实验仿真与分析

为全面验证SelfDE算法的性能，我们从最优解质量和收敛速度两方面对其进行测试，并与已有的几种差异演化改进算法分别进行了比较。

3.1 SelfDE与jDE、FADE算法的比较

为检验SelfDE算法的最优解性能，选择文献 ［14］中的9个常用函数对算法进行测试，并与jDE算法［12］和FADE算法［10］的结果比较。测试函数如表1所示，其中n表示自变量维数，S表示自变量取值范围，fmin表示函数的最优解。函数F1－F7是高维问题。其中F1，F2是单峰函数，F3是不连续函数，F4为带噪声的4次函数，F5－F7是多峰函数。F8，F9是有局部极小点的低维函数。实验中SelfDE算法的参数设置与文献 ［14］中的jDE算法设置相同：D＝50，NP＝10×D，最大迭代次数分别取F1，F3，F4，F6，F7为5000，F2为7000，F5为10000，F8为100，F9为50。

实验结果如表2所示，其中mean best为平均最优解，std－dev为标准差。表2中SelfDE的结果都取100次独立运行的平均值，jDE和FADE算法的结果取自文献 ［14］。

从表2可见，对9个测试函数，SelfDE算法所获得的最优解值都明显优于jDE和FADE算法。同时，值得说明的是在实验中，τ1，τ2的取值均为0.1。通过多次实验，我们发现τ1，τ2的取值对函数的最优结果影响是不明显的。

表1 测试函数F1－F9

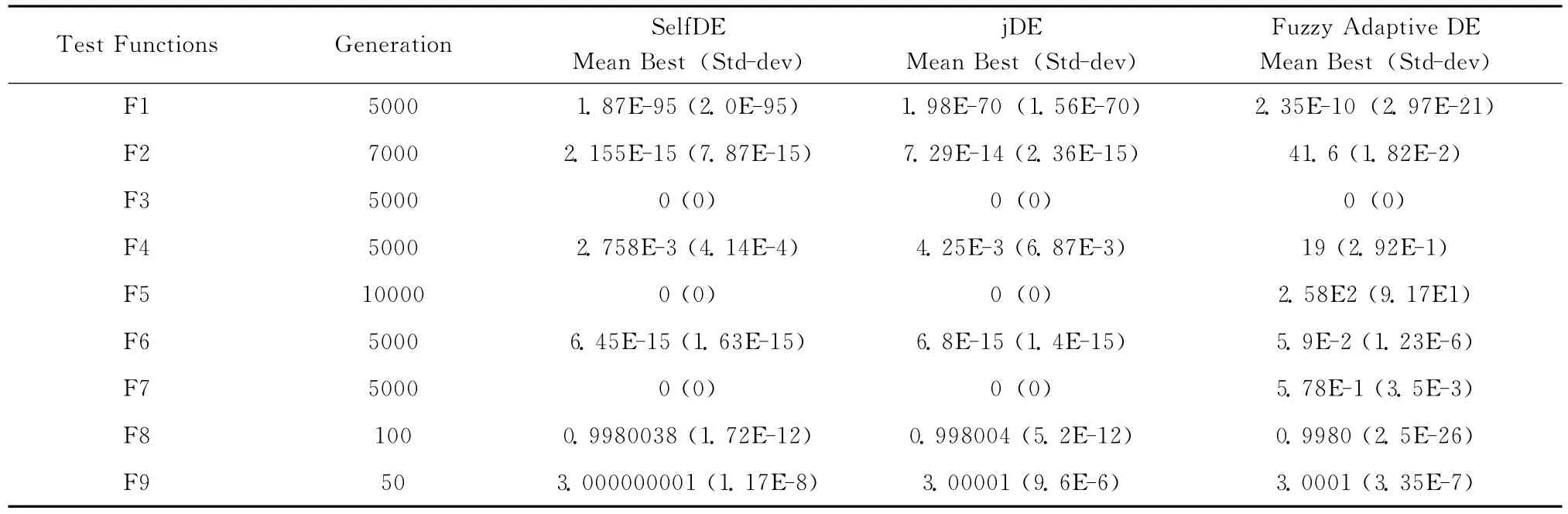
表2 函数F1－F9的运行结果

3.2 SelfDE与DDE、jDE、MPDE及DE算法的比较

为进一步检验SelfDE算法的收敛速度，对文献 ［17］中的5个常用测试函数，分别用DDE算法［18］、jDE算法［12］、MPDE算法［17］及基本DE算法对其进行比较实验。这5个测试函数如表3所示。其中，F1，F2为单峰函数，只有一个极小值。F3，F4，F5为多峰函数，都有多个局部极小值，特别是F5在全局极小点附近有无限多的次全局极小点，一般算法很难得到最优解。在实验中，除F5为2维变量外，其它4个函数都取30维变量进行测试。

为使算法运行结果可以相互比对，所有算法参数设置与文献 ［17］相同：

（1）对各函数统一设置种群规模NP＝100。

（2）对 DE、DDE、MPDE设置F＝0.5，CR＝0.9。jDE和SelfDE算法F和CR自适应调节。

（3）在MPDE算法中，根据文献 ［17］设置MP的值，对F1，F3，F4设 MP＝0.1，对F2设 MP＝0.05，F5设MP＝0.008。

实验结果如表4～表8所示，各算法的结果均为独立运行50次的平均值。

从表4～表8的实验结果可以看出，SelfDE算法对F1－F4这4个高维测试函数都取得了很好的效果，无论是搜索最优解的成功率，所需迭代的次数，以及所运行的时间都明显优于其它4种算法。对低维函数F5而言，其搜索空间远远小于高维函数，其它算法都可以很快找到最优解，因而SelfDE算法并没有特别的优势。但低维函数的搜索本身就不需要太多时间，因而SelfDE算法与其它算法的差距也是很小的。这一点从表8的实验结果中也可以看出来。

另外，从表4～表8的实验结果可知，MPDE算法的搜索效率仅次与SelfDE算法，是一种效率较高的算法，但对函数F4而言搜索到最优解的成功率较低。jDE算法虽然与SelfDE算法一样对所有5个测试函数最优解的搜索成功率均为100%，但jDE算法的搜索效率 （所需运行时间或迭代次数）远远大于SelfDE算法。因此，我们可以看到SelfDE算法在保证得到全局最优解的基础上，所需的迭代次数和搜索时间大大少于其它算法，尤其对于高维函数而言。

表3 测试函数F1－F5

表4 函数F1实验结果

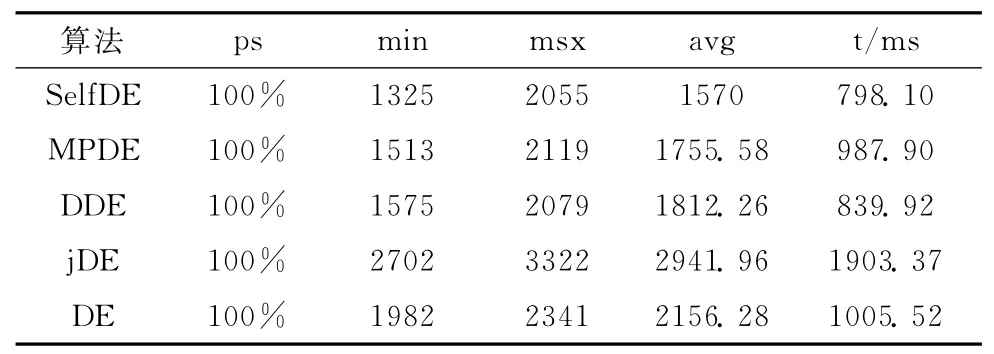
表5 函数F2实验结果

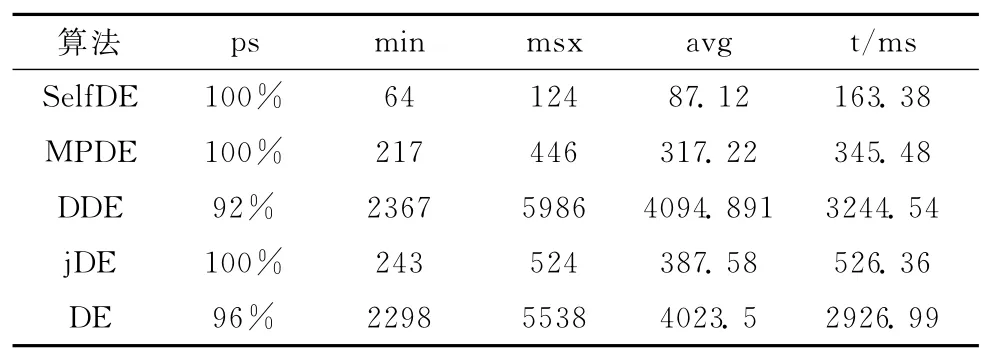
表6 函数F3实验结果

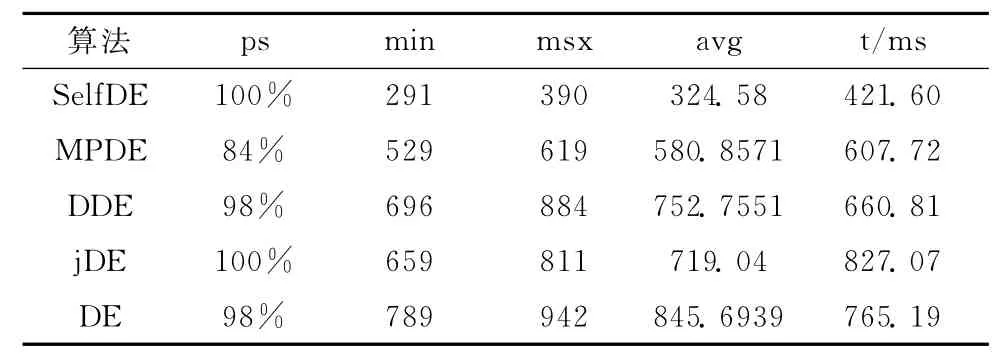
表7 函数F4实验结果

表8 函数F5实验结果

4 结束语

控制参数选取是包括差异演化在内的演化算法设计所要解决的一个重要问题。合适的控制参数对演化算法的性能有着重要影响。但针对不同的优化任务人工设置最佳的控制参数又是非常困难的，需要反复试验，计算量太大。本文提出一种自适应调整控制参数的差异演化算法 （Self－DE），自动调整DE算法中的缩放因子F和交叉因子CR，并利用交叉操作生成两个新个体与父代个体竞争形成下一代个体。不但减少了DE算法中需要人工选取的控制参数，而且加快了DE算法的收敛速度。

对测试函数的仿真实验表明，SelfDE算法在最优解质量上优于文献 ［10］和文献 ［14］中提出的两种自适应选取控制参数算法：FADE算法和jDE算法。另外，对5个常用测试函数的实验结果表明，SelfDE算法在保证收敛性的同时，大大加快了算法的收敛速度。特别是对于高维函数来说，相对于基本差异演化算法、动态差异演化算法（DDE算法）、带局部增强算法的差异演化算法 （MPDE算法）和jDE算法，该算法的性能有较大的提高。

［1］Price K，Storn R，Lampinen J.Differential evolution：A practical approach for global optimization ［M］.Berline：Springer－Verlag，2005.

［2］Alatas B，Akin E，Karci A.MODENAR：Multi－objective differential evolution algorithm for mining numeric association rules ［J］.Applied Soft Computing，2008，8 （1）：646－656.

［3］Das S，Abraham A，Konar A.Automatic clustering using an improved differential evolution algorithm ［J］.IEEE Transaction on Systems Man and Cybernetics：Part A，2008，38（1）：218－237.

［4］Feoktistov V.Differential evolution：In search of solutions［M］.Secaucus，NJ，USA：Springer－Verlag New York Inc，2006.

［5］Chakraborty U，Advances in differential evolution ［M］.Berlin：Springer－Verlag，2008.

［6］Onwubolu G C，Davendra D.Differential evolution：A handbook for global permutation－based combinatorial optimization［M］.Berlin：Springer－Verlag，2009.

［7］Storn R.Designing nonstandard filters with differential evolution ［J］.IEEE Signal Processing Magazine，2005，22 （1）：103－106

［8］Paterlini S，Krink T.Differential evolution and particle swarm optimization in partitional clustering ［J］.Computational Statistics ＆ Data Analysis，2006，50 （5）：1220－1247.

［9］FENG Qi，ZHOU Deyun.Time optimal path planning based on differential evolution algorithm ［J］.Computer Engineering and Applications，2005，41 （12）：74－75 （in Chinese）. ［冯琦，周德云.基于微分进化算法的时间最优路径规划 ［J］.计算机工程与应用，2005，41 （12）：74－75.］

［10］Liu J，Lampinen J.A fuzzy adaptive differential evolution algorithm ［J］.Soft Computing－A Fusion of Foundations，Methodologies and Applications，2005，9 （6）：448－462.

［11］Teo J.Exploring dynamic self－adaptive populations in differential evolution ［J］.Soft Computing－A Fusion of Foundations，Methodologies and Applications，2006，10 （8）：673－686.

［12］Brest J，Greiner S，Boskovic B，et al.Zumer self－adapting control parameters in differential evolution：A comparative study on numerical benchmark problems［C］.IEEE Transactions on Evolutionary Computation，2006，110 （6）646－657，ISSN：1089－778X.

［13］Qin A K，Suganthan P N.Self－adaptive differential evolution algorithm for numerical optimization ［C］.IEEE Congress on Evolutionary Computation.IEEE Press，2005：1785－1791.DOI：10.1109/CEC.2005.1554904.

［14］ZHAN Zhihui，ZHANG Jun.Self－adaptive differential evolution based on PSO learning strategy ［C］.Portland，America：Proc Genetic Evol Comput Conf，2010：39－46.

［15］Brest J，Boskovic B，Greiner S.Performance comparison of self－adaptive and adaptive differential evolution algorithms［J］.Soft Computing－A Fusion of Foundations，Methodologies and Applications，2007，11 （7）：617－629.

［16］WU Zhi－feng， HUANG Hou－kuan， ZHANG Ying. A differential evolution algorithm with double trial vectors basedon Boltzmann mechanism ［J］.Journal of Nanjing University（Natural Sciences），2008，44 （2）：195－203 （in Chinese）.［武志峰，黄厚宽，张莹.基于Boltzmann机制的双子代竞争差异演化算法 ［J］.南京大学学报 （自然科学版），2008，44（2）：195－203.］

［17］ZHAO Guang－quan，PENG Xi－yuan，SUN Ning.A modified differential evolution algorithm with local enhanced operator［J］.Acta Electronica Sinica，2007，35 （5）：849－853 （in Chinese）.［赵光权，彭喜元，孙宁.带局部增强算子的微分进化改进算法 ［J］.电子学报，2007，35 （5）：849－853.］

［18］Qing Anyong.Dynamic differential evolution strategy and applications in electromagnetic inverse scattering problems ［J］.IEEE Transactions on Geoscience and Remote Sensing，2006，44 （1）：116－125.