骨架驱动的三维模型变形方法

韩 丽，齐晓明

（辽宁师范大学 计算机与信息技术学院，辽宁 大连116029）

0 引 言

三维网格模型的变形通常指在不改变其拓扑连接的同时改变网格顶点的坐标，使得模型的姿态发生变化［1］，在几何建模和计算机动画中有着非常重要的应用。

目前主要使用的变形方法有自由变形方法，多分辨率网格变形方法和基于骨架的变形方法。基于骨架的变形方法最早由Thalmann提出，其主要思想是将三维网格的变形与人体的运动相类比，由骨架的运动带动网格表面点 （皮肤）的运动。该方法具有良好的直观性，因此被广泛应用于人体动画、游戏等领域［1］。

文献 ［2］将网格表面的点与三角曲线绑定，通过对三角曲线的变形，达到网格表面的形变；文献 ［3－4］提出了一种以单纯形为操作单元的骨架驱动变形方法；文献 ［5］则将动力学公式和有限元方法结合，对三维模型进行骨架驱动变形，取得了良好效果。以上方法均集中在单一骨架驱动的模型变形。

本文在文献 ［2］的基础上，改变了骨架约束方式以及约束区域划分方式，提出了一种新的多骨架驱动的三维模型变形方法。首先，基于Reeb图方法实现网格模型的拓扑骨架提取，其次，将多个骨架节点进行曲线拟合，并通过反求曲线控点的方式实现多骨架点驱动的骨架变换。最终，实现模型自然、光顺的变形效果。

1 变形算法及原理

1.1 骨架约束点的确定

三维模型的骨架是将三维模型的拓扑特性可视化以后形成的类似骨架且嵌于三维模型内部的图形。本文采用了文献 ［9］提出的多分辨率Reeb图的原理，进行模型的骨架提取。

定义1 设M是一个光滑的三维流形，μ：M→R是定义在模型M上的连续函数，则Reeb图是通过等价关系 （v1，μ（v1））～ （v2，μ（v2））所构成的函数μ的商空间，其中v1和v2为模型M上的任意顶点。因此，给定模型上两个顶点vi和vj，当且仅当以下条件满足，则等价关系～成立

对于曲面上的每一组等价点集合，我们使用一个节点表示，相邻节点使用边连接，从而形成了图结构，即Reeb骨架图 （RG），如图1（a）为使用高度函数作为μ函数，进行4等分区间划分所提取的Reeb图骨架。

根据Reeb图的思想，不同的连续函数μ会产生不同的Reeb图。文献 ［7］引入测地线距离作为连续函数，创建了具有平移、旋转不变性的μ函数。然而，由于需要人为选择源点来计算各个顶点的测地线距离，不同的源点选择则获得不同的Reeb图，因此，使提取的骨架具有极不稳定性。多分辨率Reeb图简称MRG进一步引入了基本点的概念，其基本思想是将μ函数定为

式中：g（v，bi）——顶点v距基本点bi的测地线距离，基本点为均匀散布在模型表面的顶点，area（bi）是每个基本点相对应的模型表面积。r相当于一个基本点占据的表面半径，r越小就会得到越多的bi基本点，MRG算法中设置（其中area（S）为模型表面积）。使用基本点作为测地线距离的源点，大大加强了测地线距离的稳定性。在模型顶点的测地线距离的g（v，bi）计算中，Dijkstra的最短路径算法被引用近似测地线距离，有效提高了运算速度。

通过应用最短路径算法，可计算网格顶点v到所有基本点bi测地线距离之和。从而，获得各个网格顶点的μ函数值μ（v）

最终，我们将μ函数值进行规一化处理为μN（v），并将μN函数值区间进行k等分，找出划分后每个区间内的子连通点集，聚合成一个骨架的关节点，最后按一定顺序连接这些关节点即生成骨架。

图1（b）示意了使用测地线距离作为连续函数μ，并进行4等分的区域划分 （如图中不同颜色所示），最终提取各等价区域的骨架节点，构成Reeb图骨架结构。

Reeb图中的每个骨架节点对应一定范围的模型顶点和面片，即子连通点集，则骨架关节点与模型面片之间就产生了绑定关系，关节点的移动就会影响到与其有绑定关系的模型面片与顶点。

1.2 多骨架驱动的三维模型变形算法

1.2.1 基于骨架点的Bézier拟合曲线

Bézier曲线采用由控制顶点组成的多边形来控制曲线的几何形状，一般地，一条n次Bézier曲线可以表示为

图1 多分辨率Reeb图

本文中，我们利用Bézier曲线的端点插值性、凸包性［8］及连续性［9］等性质，首先将骨架节点作为控制顶点，构造Bézier拟合曲线，然后由任意一控点 （骨架点）变化，得出新的Bézier曲线，最后反求Bézier曲线上其它控点，从而更新多骨架点的空间坐标，实现了基于Bézier曲线的多骨架点连续、光顺变形。

我们以3个连续的骨架点作为控点为例，进行二次Bézier曲线拟合，并依据曲线上的任意点Qi的变化，更新控点坐标P1，其具体过程如图2所示。

图2 插值的二次Bézier曲线

二次Bézier曲线P（t）

已知曲线上3个顶点Qi（xi，yi，zi） （i＝0，1，2），其中Q0＝P0，Q2＝P2，点Q1可由，l2＝，根据获得。将Q1带入式 （5），即可求得控点P1

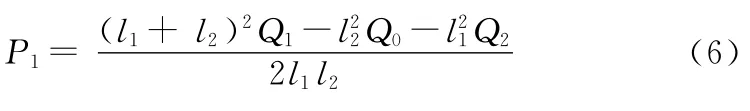
1.2.2 3个骨架点的变换

假设空间中3个骨架点Pi（xi，yi，zi），i＝0，1，2，当P0点保持固定不变时，移动点P2到点P2′时，点P1对应的新位置P1′的计算方法如下：

（1）确定曲线上Q1点的位置；

1）确定参数tQ的值。令则；

2）根据式 （5）计算Q1的坐标，即Q1＝P（tQ）；

（2）计算点P2移到点P2′的移动向量；

（3）计算Q1变化的新坐标，其Q1′＝Q1＋t＊vec；

（4）根据更新的Q1点坐标可获得控点P1的变化 （如图3所示）。令，则依据式（6），可得：。

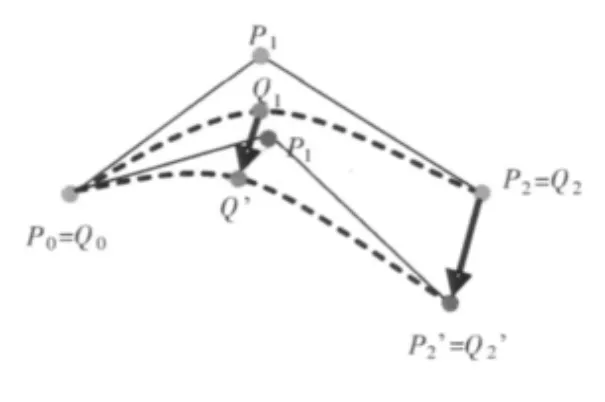
图3 3个骨架节点变化算法

该算法中，首先确定Bézier曲线上的点Q1，并进行矢量方向的空间变换，从而获得新的曲线，最终反求获得骨架点P1的变化。由算法步骤 （1）中的可知，参数tQ的取值直接关系到点Q1的位置和控点P1的更新。本算法中，tQ定义为点P1到点P0的距离与其分别到点P0和点P2的距离和的比值，实验证明，这样的取值方法比较tQ随机的取值具有更自然的效果。

如图4所示，黄色点为原始的3个骨架控点，通过拉动右侧节点P2到新的空间位置，则节点P1的位置发生变化 （红色点为更新后的控点）。图4（a）、图4（b）为人为设定tQ值，控点的变化结果；图4（c）为依据本算法计算tQ所获得的控点，相比较图4（a）、图4（b）效果，其位置变化更加自然、合理。

算法充分利用了二次Bézier曲线的一阶连续性，保证了骨架节点位置的变动更加平滑自然。

1.2.3 多骨架点驱动的变换方法

将1.2.2节中描述的算法应用于多个骨架节点，即可得到多骨架节点的连续平滑变化。

在算法中，选定P0至Pn－1n个骨架节点，已知节点Pn－1的位置变化，先以Pn－3，Pn－2，Pn－1这3个节点为一个单元，计算出参数t，以及Pn－2的位置变化，然后以循环的方式分别获得Pn－3至P1点的位置变化。算法中，以3个骨架节点为单元，t的值是与其所处单元中3个节点的位置相关的，从而更加保证节点变化的平滑性。图5显示了多个骨架节点运用上述算法进行变换后的效果。

图4 tQ取不同值时骨架控点的变化

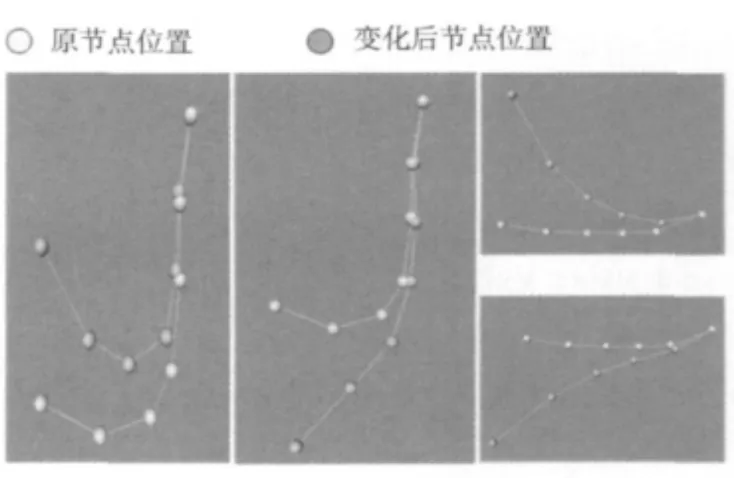
图5 多节点骨架变换

1.3 多骨架点驱动的模型变形

为了使模型表面变形更具光滑性及连续性，在此引入具有势函数的元球。

定义2 设模型空间R3上任意点v＝ （x，y，z），Deform（v）为变形映射，它把点v变换到v′，Δv为v点的偏移量。依据广义元球约束变形原理，单个约束源Pi引起的变形函数可定义为

式中：r（v，Pi）——模型上任意点v到约束中心点Pi（约束源）的欧式距离，f（r，Ri）——定义于半径为Ri的元球上的势函数。目前采用的势函数基本有4种：Borrel的幂函数、Nishimura的分段二项式、Murakami的四次多项式、Wyvill的六次多项式［17］。本文采用了变形效果较好的Wyvill的六次多项式作为势函数

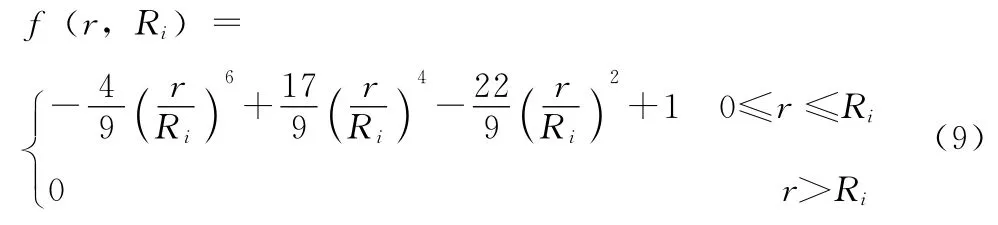
从函数f（r，Ri）中可以看出约束源Pi在约束半径R下定义了一个局部区域，在r≤Ri的区域内，多边形模型网格点会受到约束源的影响，而对于这个局部区域外的点，则不会出现位置的变化。Wyvill的势函数有效保证了变形效果的局部性与光顺性。

在变形过程中，用户所选的骨架关节点，即为约束源Si，i＝0，1，2……n－1，约束半径R则由关节点到其所对应的区域的最大欧氏距离来确定

假设Pi＝ （xi，yi，zi）为选中的骨架关节点Si（约束源）所对应的连通区域上点，d（dx，dy，dz）是约束源S的偏移量 （可由用户交互式拖拽操作完成），Displacement（p）是平移变形映射，则有以下计算公式

这样，在牵动最后一个关节点移动后，就会得到与之相连的多个骨架节点的以及其周围面片相应的动画变形。

骨架节点约束的区域变形算法描述如下：

typedef struct SubConnectPointSet//连通子集定义

｛ VNode＊＊connective＿VNode；

struct SubConnectPointSet＊next；

｝SubConnectPointSet；

typedef struct VNode //模型顶点定义

｛ float x，y，z；//模型顶点的空间坐标值

void＊belongtoSCPS；//该顶点所属的子连通点集

｝VNode；

typedef struct SkeletonJoint//骨架节点定义

｛float x，y，z；//骨架节点的坐标

SubConnectPointSet＊belongtoSCPS；//该节点所属的子连通点集。

｝SkeletonJoint；

算法步骤：

（1）交互式确定骨架节点，获取约束源的坐标SkeletonJoint＊S；

（2）遍历骨架点所对应的区域 （S－＞belongtoSCPS－＞connective＿VNode），计算区域中各顶点VNode＊vi距约束源S的欧式距离r：r（vi，S）；

（3）获得约束区域的最大欧氏距离作为约束半径R：R＝Max（r（vi，S））；

（4）计算对应区域上顶点VNode＊vi的势函数：f（r，；

（5）交互式拖拽骨架点S进行空间平移d（dx，dy，dz），进行相应区域顶点的转换，生成新的空间坐标：Displacement（vi）＝vi＋d＊f（r，R）。

图6是针对同一个长方体模型进行骨架驱动变形的结果。图6（a）为提取的长方体的骨架；图6（b）、图6（c）为通过对骨架进行交互式变形，获取各骨架点的空间位移。图6（d）为骨架空间位移后获取的变形效果。图7则显示了对鞋模型进行骨架驱动变形的效果。

2 实验结果

我们在奔腾Ⅳ2.8GHz，1G内存的PC机上，以MFC和OpenGL图形库为基础，使用VC＋＋6.0作为开发环境，进行了本算法的验证。

本算法中测地线距离是利用Dijkstra最短路径近似得到，它的时间复杂度为O（NlogN），N代表模型顶点总个数。构建骨架关节点 （即子连通点集），所需消耗O（N）的时间复杂度。对于各个骨架点对应的模型子区域以及其势函数与偏移量的计算为O（M），M（M＜N）为各子区域所对应的模型顶点的平均数。因此，算法总的时间复杂度为O（NlogN）。表1为本算法的实验性能分析。

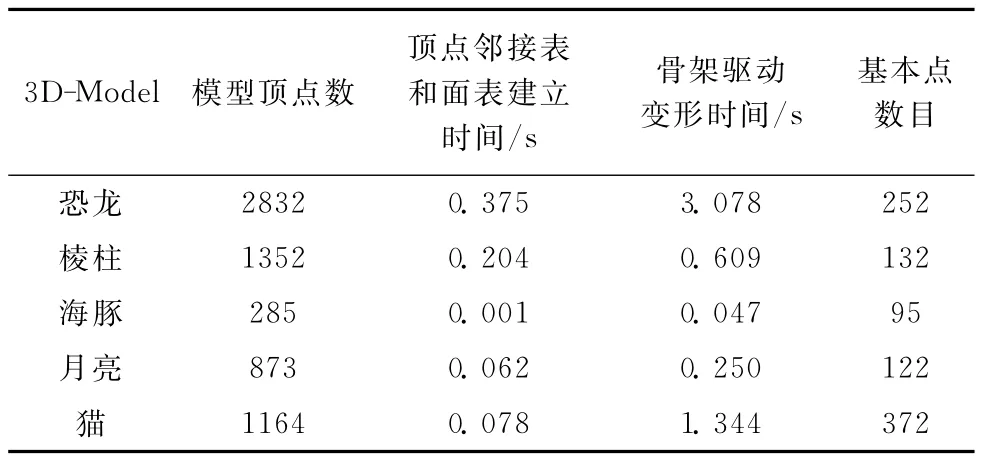
表1 算法运行特性分析

如表2所示，我们使用测地线距离对模型进行分割并提取骨架关节点。然后，使用交互方式确定需要变形区域的多个约束关节点，采用拖拽末端骨架关节点的直观方式实现局部区域的变形。表2中 （1）行所示为棱柱模型的变形，我们把棱柱模型分6区间提取Reeb图骨架，然后选取棱柱上部4个骨架节点为驱动节点，对棱柱进行变形，在此结果的基础上我们继续在上部选取3个骨架节点、在下部选取4个骨架节点分别进行多骨架节点驱动变形，得到了中间和右边的变形结果。

在表2中（2）行，展示了对海豚模型提取骨架后，选取头部4个骨架节点进行变形的效果；在表2中 （3）行，对月亮模型提取骨架并选取其面部鼻梁处的4个骨架节点进行驱动，得到了月亮模型面部的平滑变形。表2中 （4）为将猫模型提取骨架后分别对去上肢和双腿进行变形的结果。

?

3 结束语

本文基于Bézier曲线的拟合的方法提出了多骨架点驱动的交互式局部变形方法。我们通过多分辨率Reeb图骨架的提取方法，可以对所有模型进行骨架提取，并且确定了骨关节点与骨架所对应的局部约束区域，通过交互式拖动实现基于多骨架点的局部变形。有效地保持了模型的局部特征，确保了模型动画的直观性、高效性。且在提取骨架时所需分层数目和需要驱动的骨架节点的数目都可以交互式的灵活确定，使得使用十分方便简单。通过实验证明，该算法计算量小，易于控制。此方法可通用在计算机造型、动画、游戏以及电影特效中。

［1］HU Shimin，YANG Yongliang，LAI Yukun.Research progress of digital geometry processing ［J］.Chinese Journal of Computers，2009，32 （8）：1451－1469 （in Chinese）. ［胡事民，杨永亮，来煜坤，数字几何处理研究进展 ［J］.计算机学报，2009，32 （8）：1451－1469.］

［2］Sven Forstmann，Jun Ohya.Fast Seletal animation by skinned arc－spline based deformation ［C］.Eurographics，2006.

［3］YAN Hanbing，HU Shimin，Ralph Martin.Skeleton－based shape deformation using simplex transformations ［G］.LNCS 4035：Proceedings of Computer Graphics International.Berlin Heidelberg：Springer－Verlag，2006：66－77.

［4］YAN Hanbing，HU Shimin，Ralph R Martin，et al.Shape deformation using a skeleton to drive simplex transformations［J］.IEEE Transactions on Visualization and Computer Graphics，2008，14 （3）：693－706.

［5］SONG Chao，ZHANG Hongxin，HUANG Jin，et al.Fast and physical plausible elastic－deformation driven by skeleton［J］.Chinese Journal of Computers，2006，29 （12）：2194－2200（in Chinese）.［宋超，张宏鑫，黄劲，等.骨架驱动的快速似然弹性变形 ［J］.计 算 机 学 报，2006，29 （12）：2194－2200.］

［6］HAN Li，CHU Bingzhi，GAO Xiaoshan.Gaussian curvature constrained skeleton extraction method based on MRG ［J］.Journal of Computer－Aided Design ＆ Computer Graphics，2009，21 （9）：1227－1231 （in Chinese）. ［韩丽，楚秉智，高小山.高斯曲率约束的MRG骨架提取优化算法 ［J］.计算机辅助设计与图形学学报，2009，21 （9）：1227－1231.］

［7］Lazarus F，Verroust A.Level set diagrams of polyhedral objects［C］.Proceeding of 5th ACM Symp Solid Modeling and Applications，1999：130－140.

［8］Donald Hearn，Pauline Baker M.Computer graphics ［M］.CAI Shijie，WU Chunrong，SUN Zhengxing，transl.2nd ed.Beijing：Electronic Industry Press，2002 （in Chinese）.［Donald Hearn，Pauline Baker M.计算机图形学 ［M］.蔡士杰，吴春镕，孙正兴，译.2版.北京：电子工业出版社，2002.］

［9］Francis S Hill Jr，Stephen M Kelley.Computer graphics using OpenGL ［M］.HU Shimin，LIU Ligang，LIU Yongjin，et al transl.3rd ed.Beijing：Tsinghua University Press，2009 （in Chinese）.［Francis S Hill，Stephen M Kelley Jr.计算机图形学 （OpenGL版）［M］.胡事民，刘利刚，刘永进，等译.3版.北京：清华大学出版社，2009.］

［10］PENG Q S，JIN X G，WAN H G，et al.The basis of computer graphics applications ［M］.Beijing：Science Press，2009（in Chinese）.［彭群生，金小刚，万华根，等.计算机图形学应用基础 ［M］.北京：科学出版社，2009.］

［11］Alvaro E，Cuno Parari，Claudio Esperanca.Shape－sensitive MLS deformation ［J］.Vis Comput，2009，25 （10）：911－922.