无线传感器网络在机械振动监测中的应用*

黄荣久，方 杰，刘 煜

（重庆大学 通信与测控中心，重庆 400044）

0 引言

随着机械设备的精密程度、复杂程度及自动化程度越来越高，机械设备状态监测和故障诊断技术越来越受到重视。而机械振动是机械设备运行中的一个重要特征参数，机械振动监测是机械设备状态监测和故障诊断的重要手段。无线传感器网络（wireless sensor networks，WSNs）［1，2］技术的发展，使得其越来越多地应用在测试测量工程领域。

用无线传感器网络取代传统有线传感器装置，可以减少布线，降低监测系统部署成本，增加监测系统的灵活性、可维护性和可扩展性。同时，无线传感器网络具有较强的容错能力，从而使监测系统的鲁棒性提高。传感器节点可以移动，拓扑结构具有动态性。鉴于无线传感器网络的种种优点，其在机械振动监测系统中的应用研究成为业界的关注热点［3～5］。

针对机械振动监测的现状，结合无线传感器网络技术的发展，构建机械振动监测无线传感器网络系统模型及其网络拓扑结构，并采用关系矩阵算法完成对监测数据的融合，以提高监测精度和减少传输的数据量，最终完成对机械振动的实时监测。

1 机械振动监测无线传感器网络系统模型

机械振动监测无线传感器网络系统由机械振动信号采集、数据传输、数据管理三部分组成，如图1所示。整个监测系统是由多个相对独立的微型监测子网组成的无线传感器网络。在机械振动信号的采集部分，以一定数量的监测节点分布于监测区域内进行数据采集，通过一定的组网方式构成无线传感器网络。每个监测节点完成振动数据的采集，采集到的数据发送到网关节点，网关节点在网络中起数据汇集点的作用，最终传送到数据终端进行下一步的数据处理，同时在监控端通过分析接收到的振动数据，可以监测机械设备的振动情况和对机械设备出现的故障进行诊断。

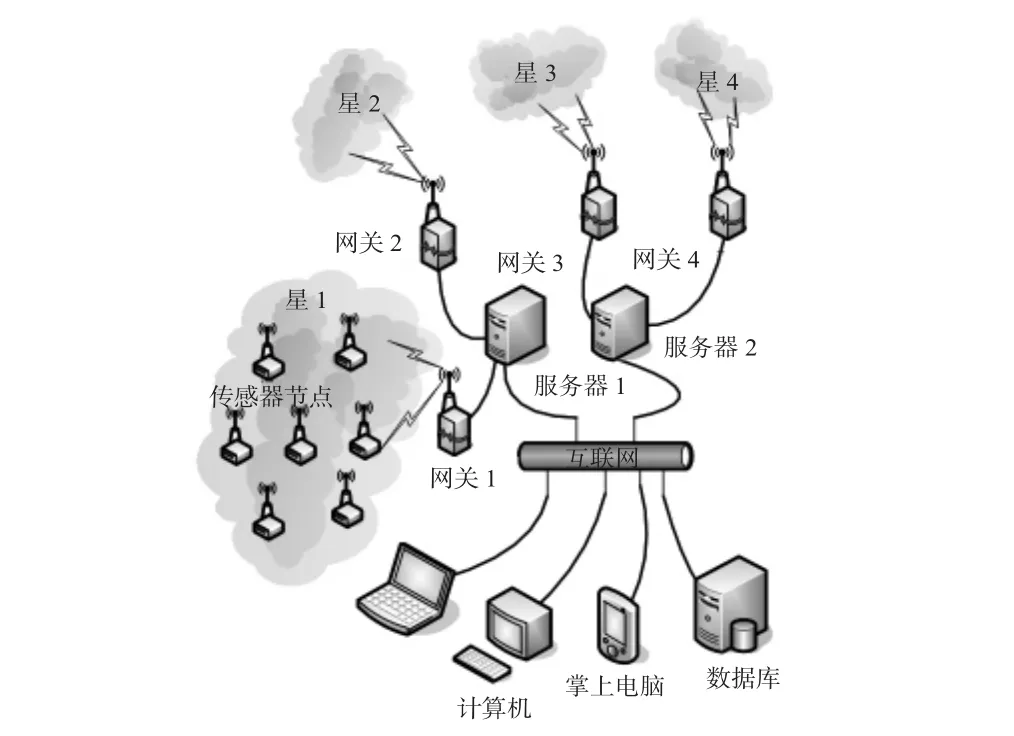
图1 机械振动监测无线传感器网络系统模型Fig 1 WSNs system model for mechanical vibration monitoring

在机械振动监测系统中，及时而准确地获取振动信号是完成监测和诊断的前提条件。为保证较高的振动信号品质和采集可靠性，采取以现有的测振传感器和信号预处理电路与无线网络节点结合的监测模式［6］，将所采集到的机械部件振动信号在前端电路预处理后，接入无线网络节点端进行A/D转换，最终通过无线通信模块完成数据传输。监测节点硬件组成如图2所示。

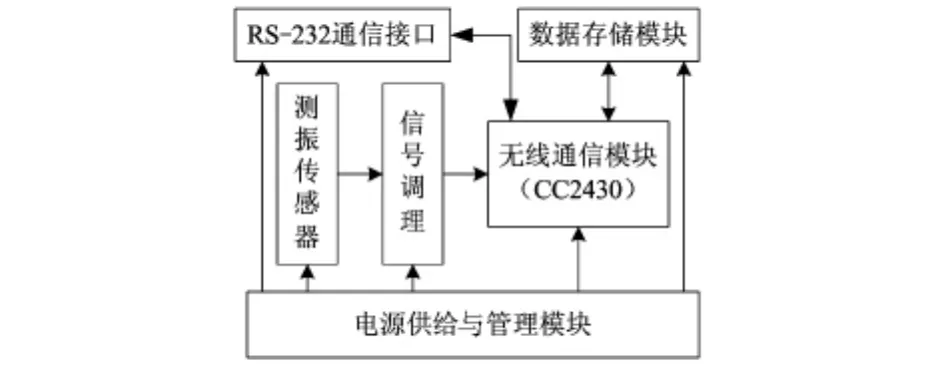
图2 监测节点的硬件组成Fig 2 Hardware composition of monitoring node

2 机械振动监测无线传感器网络拓扑结构

在机械振动监测无线传感器网络系统中，无线传感器网络的设计相对其他的工程应用有所不同，机械振动测试中，被测对象要求的测量点数通常在几十个节点左右，这与常规的无线传感器网络中以大量节点为基础的大规模组网概念不同，网络的覆盖范围相对于环境监测等传统应用要小得多。传统的无线传感器网络随机布点、自组网所形成的网络拓扑结构在机械振动无线传感器网络中并不适用。因此，采取人工布点方式，通过IEEE 802.15.4协议组建星型拓扑结构网络，如图3所示。

星型拓扑结构是最简单的一种网络拓扑形式，这种拓扑结构只包含一个协调器节点和一系列的终端设备节点。每个终端设备节点只能和协调器节点进行通信。在本机械振动监测系统中，依据机械设备的运行情况，在需要监测的部位部署若干个监测节点，监测节点和网关节点组成星型拓扑结构的监测子网，监测节点作为终端设备节点负责对机械振动监测数据的采集，网关节点作为协调器节点则是整个星型网络的中心，负责对整个星型监测网络内各节点的维护与数据转发，为了防止由于网关节点损坏或者能量耗尽导致整个监测子网失效，采用一个具有全功能的节点作备用网关，在网关节点出现异常情况下作网关节点使用，直到原网关节点恢复正常功能。

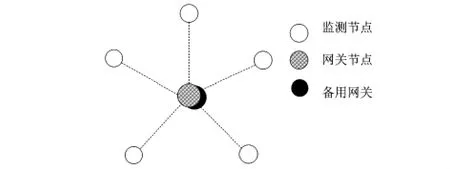
图3 机械振动监测无线传感器网络拓扑结构Fig 3 Structure of WSNs topology for mechanical vibration monitoring

3 机械振动监测数据融合

机械振动监测无线传感器网络有别于传统的无线传感器网络，网络规模相对较小，节点个数不是太多。在选定星型拓扑结构作为监测子网的组网方式的前提下，网络路由就相对简单，通过网关节点转发即可，在这里不作详细论述。但是，机械振动监测无线传感器网络数据信息大，要求网络时延小。如果把每个节点的数据都通过网关节点发送到监测终端，不仅会导致网络拥塞产生较大的数据延迟，还会不必要地过分消耗能量致使网络生命周期缩短。因此，数据融合是机械振动监测无线传感器网络的关键。

在本系统中机械振动监测数据融合的基本思想是:若1个监测节点的输出数据被大多数监测节点所信任，即这个监测节点的输出数据有效。若1个监测节点的输出数据不被其他监测节点所信任，或者只被少数监测节点所信任，则这个监测节点的输出数据无效。采用关系矩阵法将各监测节点的输出数据依据信任程度在网关节点进行数据融合。关系矩阵法广泛用在数据挖掘、人工智能、航空航天等涉及到大量数据信息处理的各个领域［7～9］。

设监测子网由n个监测节点组成，第i个监测节点和第j个监测节点输出的数据分别是xi，xj，且都服从Gauss分布，密度函数分别记为pi（x），pj（x），xi，xj是Xi，Xj的一次观测值。为反映各监测节点数据之间的偏差大小，引进置信距离测度来表示［10］

其中

A，B分别为概率密度函数曲线pi（x|xi），pj（x|xj）在区间（xi，xj）或（xj，xij）上积分所得交集部分，分别如图4中的（a），（b）两部分图形所示。

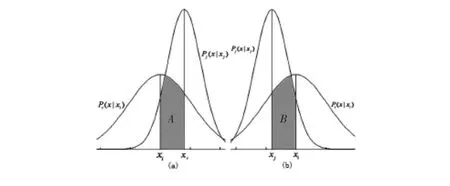
图4 置信距离测度示意图Fig 4 Schematic diagram of the confidence distance measurement

dij的值为第i只传感器与第j只传感器输出的置信距离测度。dij越小，i，j传感器之间输出数据越接近，通常dij可通过误差函数erf（θ）直接求得，即

根据关系矩阵的基本原理，结合无线传感器网络的实际物理意义，引入信任程度rij，rij表示第j个监测节点对第i个监测节点的信任程度，所有的信任程度构成关系矩阵

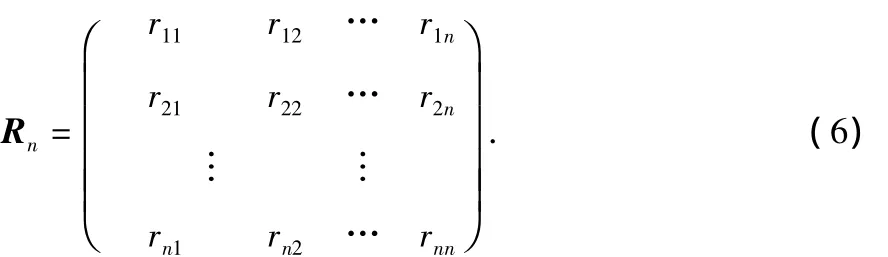
使用椭圆曲线来确定各监测节点之间的信任程度。根据节点测量的范围，确定3个阈值ε，ε1，ε2，然后结合置信距离测度，用椭圆曲线来确定rij在阈值附近的模糊性，即

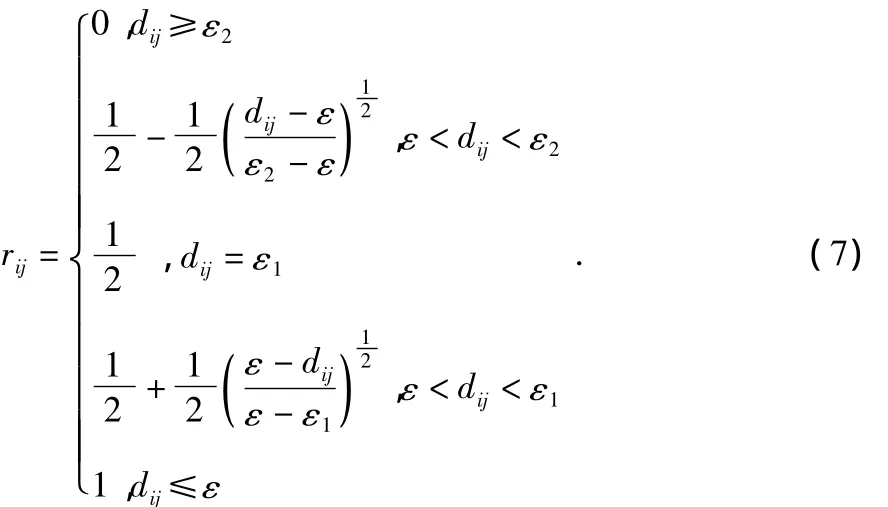
设βK是第k个监测节点在整个监测子网中的综合信任程度的衡量指标，βK值越大，该监测节点的输出数据重要程度越高，在融合过程中所占的比重越大。因为关系矩阵是正矩阵，由Perron-Frobenius定理可知，一定存在最大特征值λmax＞0。记特征方程为

解特征方程得关系矩阵的各特征值，找出其最大的特征值λmax，λmax对应的特征向量记为P，即有λmaxP=P，其中，P=［θ1，θ2，…，θn］T。展开关系矩阵可以得到

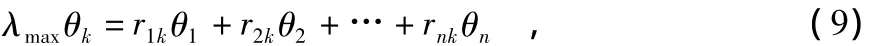
则相对应的综合信任程度为

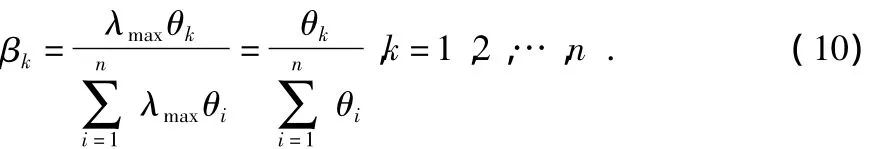
因此，监测子网内所有监测节点的输出数据在网关节点融合后的输出为

4 实验结果

为验证本系统在机械振动监测中的可用性，在实验室环境下搭建实验平台。选用Lance公司的LC0401型加速度传感器和信号调理箱获取振动信号，并利用CC2430无线通信模块自带的A/D实现振动信号的采集，以某摩托车车架为测试对象构建实验平台，其结构示意图如图5所示。

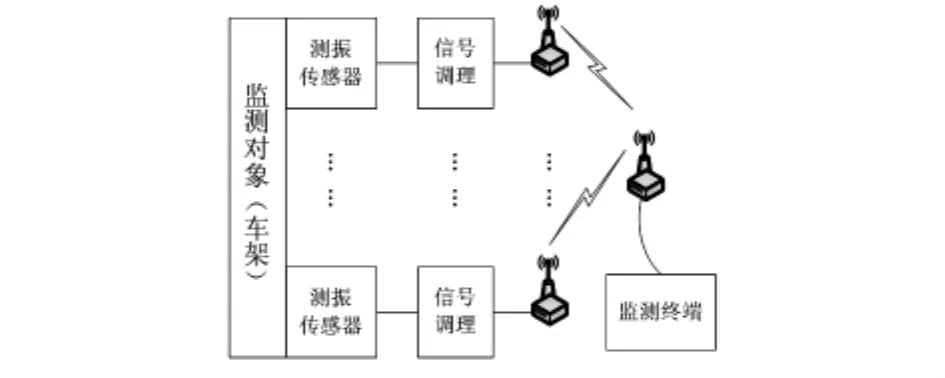
图5 实验平台结构图Fig 5 Structure diagram of experimental platform

在测试车架上，4个不同的监测部位分别具有不同的振动频率，为提高测试的准确性和鲁棒性，每个监测部位由4个监测节点构建1个监测子网，测试结果如表1所示。

从实验结果中可以看出:监测子网1和监测子网3内的各个监测节点都处于正常工作状态，由于噪声和系统误差影响，测量结果距实际振动频率有一定的偏差，但是经网关节点进行融合后，其输出相比单个监测节点更为接近实际真值，监测精度得到了大大的提高。监测子网2内的2号监测节点由于受到损坏不能正常工作，其他3个节点正常，同样，经网关节点融合去除错误数据后，其输出数据正常，证明使用关系矩阵融合的该监测网络具有很好的鲁棒性。在监测子网4所监测的部位正常状态下其振动频率为50kHz，由监测网络测得实际振动频率为44.81 kHz，系统工作异常，可以使工作人员及早发现被监测设备的故障。每个监测子网内的监测节点的监测数据经网关节点融合之后，由网关节点发送到监测终端，有效地减少了传输的数据量。

5 结论

依据无线传感器网络在机械振动监测应用中特点，构建了基于无线传感器网络的机械振动监测模型和网络拓扑结构，并通过搭建实验平台进行测试验证，表明该机械振动监测无线传感器网络系统可以完成机械振动测试任务，且具有较高的鲁棒性。同时，基于关系矩阵的数据融合算法可以有效提高监测精度和减少数据传输量。

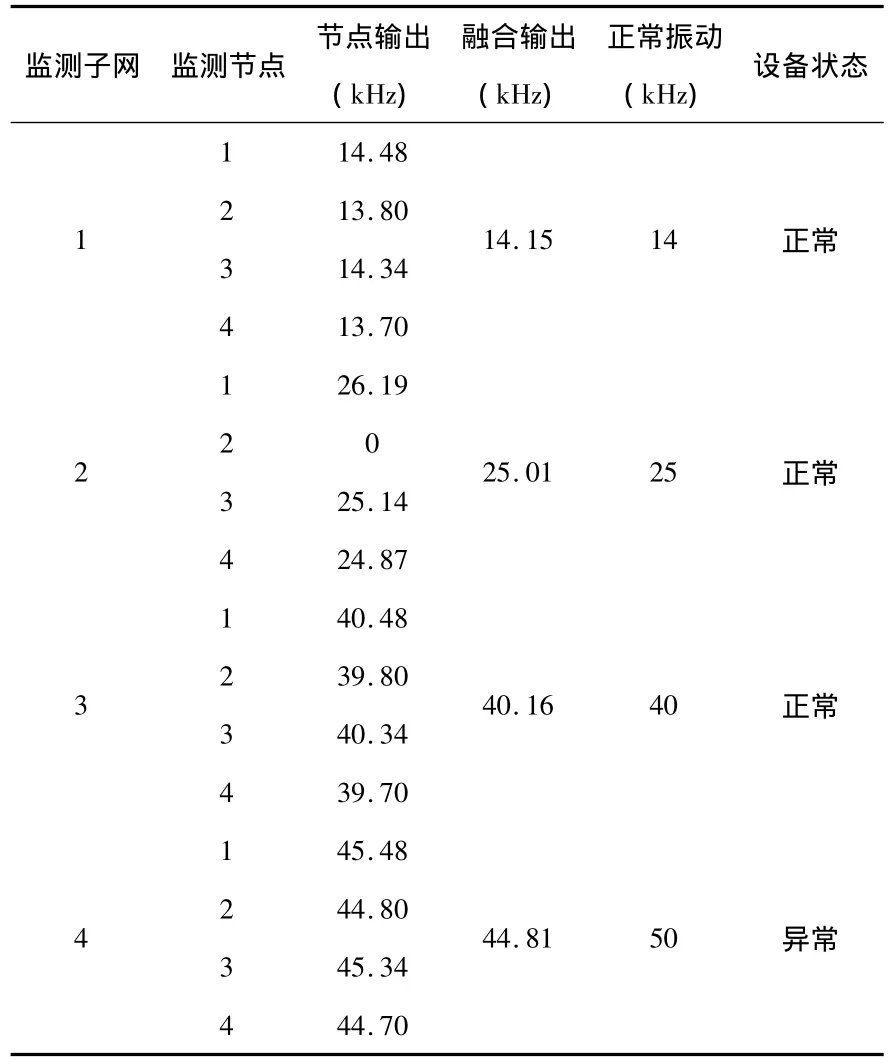
表1 监测实验结果Tab 1 Result of monitoring experiment

［1］Hill J，Culler D.A wireless platform for deeply embedded networks［J］.IEEE Micro，2002，22（6）:12 －24.

［2］Pottie G，Kaiser W.Wireless sensor networks［J］.Communications of the ACM，2000，43（5）:551 －558.

［3］Bao Wen，Zhou Rui.Anti-aliasing lifting scheme for mechanical vibration fault feature extraction［J］.Mechanical Systems and Signal Processing，2009，23（5）:1458 －1473.

［4］Huang Weiguo，Wu Shuyou.Research on blind source separation for machine vibrations arora［J］.Wireless Sensor Networks，2009，1:453－457.

［5］Rahim I A.Development of a vibration measuring unit using a micro-electro-mechanical system accelerometer for machine condition monitoring［J］.European Journal of Scientific Research，2009，35（1）:150 －158.

［6］汤宝平，贺 超.基于无线传感器网络的机械振动监测模式［J］.中国机械工程，2009，20（22）:2737 －2741.

［7］Guo Yu，Chen Wenlong，Chen Shouyu.Intelligent control and automation［C］//The 7th World Congress on Intelligent Control and Automation，WCICA 2008，2008:7108 －7112.

［8］Lin Chijen，Wu Weiwen.A causal analytical method for group decision-making under fuzzy environmen［J］.Expert Systems with Applications，2008，34（1）:205 －213.

［9］陶文华，叶志锋.关系矩阵法在发动机执行机构故障检测中的应用［J］.航空动力学报，2009，24（8）:1872 －1877.

［10］Wang C M，Iyer H K.Fiducial intervals for the magnitude of a complex-valued quantity［J］.Metrologia，2009，46（1）:81 －86.