基于核函数的PLS丁苯橡胶聚合转化率软测量*

李 炜，徐鸿飞，倪 源

（1.兰州理工大学 电气工程与信息工程学院，甘肃兰州 730050;2.兰州石化公司自动化研究院，甘肃兰州 730060）

0 引言

工业合成橡胶中，聚合转化率是衡量丁苯橡胶（styrene-butadiene rubber，SBR）产品质量的重要指标，它表示反应单体转化为高分子的百分比，对于该指标的监测，目前国内尚无合适的在线分析仪器。国内橡胶厂对其测定多采用干物质法，由于该方法存在严重的滞后性，往往成为制约产品质量和生产效益的主要因素。软测量技术的发展无疑可为丁苯橡胶聚合转化率实时预测提供一条良好的途径。

近年来，采用软测量技术对丁苯橡胶质量指标进行在线预测已有了一些初步成果［1～4］。文献［1，2］经过对丁苯橡胶工艺深入分析，确定了影响橡胶门尼粘度的主要变量，在对其进行主元分析（principal component analysis，PCA）的基础上，结合BP神经网络与LSSVM算法，分别建立了PCA-BP和PCA-LSSVM的门尼粘度软测量模型。文献［3］先通过胶浆压差、胶浆温度和环境温度三信号获得丁苯橡胶胶浆密度，再通过密度和其他项构建了丁苯橡胶聚合率的线性预测模型。文献［4］根据集成学习可以提高弱学习器预测能力的思想，首先采用bagging方法建立多个LSSVM弱学习器，然后使用AdaBoost.RT方法对bagging集成进行修剪，进而将修剪出的弱学习器加权输出，并将其用于丁苯橡胶聚合转化率的预测。然而，由于PCA在信息提取时只考虑自变量数据本身，不仅会使对数据信息的利用有所遗漏，而且，PCA本质上是一种线性特征提取方法，也不利于辅助变量间深层次非线性特征的提取;文献［3］不仅需要先后两次确立模型参数，而且，模型仍以线性回归近似，致使误差难免会被放大;文献［4］的算法则相对复杂，不便于操作实现。

相对PCA，PLS则在信息提取中同时考虑了输入输出数据集，对自变量、因变量数据交替的正交分解，使得PLS能够从较少的载荷矢量中得到尽可能多的信息［5］。但是，PLS本质上仍是一种线性算法，在处理非线性问题时仍显得力不从心。鉴于核技术在SVM中的成功应用，学者们将核的理论与 PLS相结合形成了 Kernel PLS［6，7］，其原理是先将输入数据集通过核函数映射到高维特征空间，在特征空间再运用线性PLS算法，这样特征空间的线性PLS就对应原始空间的非线性关系［8，9］，从而提高了PLS处理非线性问题的能力。然而将Kernel PLS方法用于软测量的成果还非常有限［10，11］。

基于此，本文针对某石化企业丁苯橡胶聚合转化率难以在线检测的问题，在对工艺进行了深入分析获取了辅助变量的基础上，分别建立了基于径向基核（rbf-kernel）、多项式核（poly-kernel）以及2种核函数混合核（mix-kernel）的PLS丁苯橡胶聚合转化率软测量模型。工业生产数据仿真结果表明，基于KPLS模型可提高PLS的非线性问题处理能力，预测精度能满足企业对预测精度的要求，其中mix_kernelPLS模型的预测效果在满足企业要求的同时还有一定裕度。

1 KPLS算法简介

1.1 PLS算法分析与改进

对给定的样本集，自变量数据矩阵X∈RL×m，因变量数据矩阵Y∈RL×p，L为样本数，m和p分别为自变量和因变量的维数，PLS可由外部关系和内部关系描述，其中

外部关系为

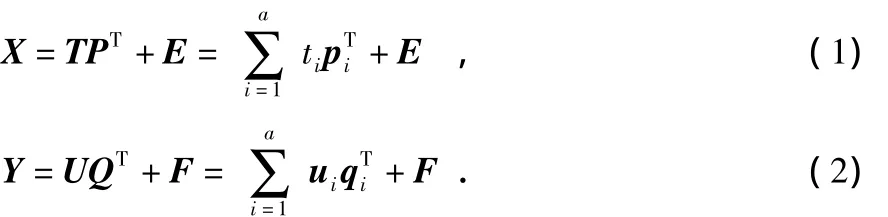
表示将X，Y分别分解为特征向量（t和u）、负荷向量（p和q）及残差（E和F），其中，i=1，…，a，a为提取特征向量个数。

内部关系为

从上述关系可知，PLS在信息提取时同时考虑输入输出数据集，通过成分提取和空间压缩技术克服噪声和变量间的相关性，并能根据正常工况的生产数据，准确捕捉自变量和因变量之间的关系。但由式（3）可知，PLS本质上仍是一种线性算法，在处理较强非线性问题时效果则不尽人意。实际工业生产中变量数据间多含有非线性成分，为增强PLS的非线性处理能力，业界主要以以下2种思想对其进行了改进:

1）基于内部非线性映射的改进其思想是保留基本PLS外部关系不变，过程中构造内部U，T间的非线性映射f（·），满足U=f（T），其中，f（·）可以是任意非线性函数或映射，目前应用较多的为神经网络。

2）基于核函数的改进

其思想是在基本PLS算法对数据处理之前，构造非线性映射（如高斯型核函数）将输入样本集映射到高维的特征空间，在特征空间中再运用基本PLS迭代算法求解，从而形成了KPLS算法。

尽管2种改进均能提高PLS的非线性处理能力，但方法2明显易于操作，不会涉及方法1中非线性函数难以确定的问题，如神经网络结构、参数等。

1.2 KPLS 算法

KPLS是通过核运算的非线性映射功能，将原始空间的数据变量映射为高维特征空间中的数据变量，然后在高维的特征空间再运用线性的PLS算法，因此，高维特征空间的线性PLS也就等价于原始空间的非线性关系，它本质是PLS算法的一种拓展，其推演过程如下:

定义非线性映射Φ（·），将原始空间的输入向量xi∈RP，i=1，…，L映射为高维特征空间的 Φ（xi）∈Rf，即

使用核技术，令K=ΦΦT。在高纬的特征空间中，非线性迭代KPLS算法可表示如下:

1）初始化向量u;

2）t=KY，t←t/‖t‖;

3）c=YTt;

4）u=Yc，u←u/‖u‖;

5）满足收敛条件转下一步，否则，转步骤（2）;

6）K←（I－ttT）K（I－ttT），Y←Y－ttTY。

迭代停止准则为:是否达到最大主元数，或者‖Y‖是否小于预设阈值。回归系数矩阵B可表示如下

式中 矩阵T，U分别由t，u构成。

对测试样本集{xi，yi}li=1，（l为测试样本集长度）其预测值为

核函数的选取对预测精度的影响较大，最常用的为poly-kernel和tbf-kernel，另外，考虑到多核间的优势互补性，也可将多个核结合，进而构造出mix-kernel以适应更为复杂的工况。

2 KPLS在丁苯橡胶聚合转化率预测中的应用

2.1 工艺简介与辅助变量选取

1）工艺简介

某石化公司（5.5×104t/a）丁苯橡胶生产装置采用低温乳液聚合方法，以丁二烯和苯乙烯为单体，反应釜在一定工艺条件下进行乳液聚合反应。当丁苯橡胶聚合转化率（或门尼值）达到要求时，终止聚合，除去并回收未反应的单体即得到胶乳;之后向胶乳中加入抗老化剂，控制凝聚条件进行凝聚。最后，将凝聚物经过皂化、洗涤、挤压脱水、干燥、成型及包装等工序，即得到相应的成品橡胶。丁苯橡胶装置的生产流程如图1所示。

图1 丁苯橡胶生产流程简图Fig 1 Production flow chart of SBR

由上工艺可知，聚合反应过程中的丁苯橡胶聚合转化率是影响产品质量的重要指标，需对其进行精确实时监测方可保证产品的质量。

2）辅助变量确定和检测

辅助变量的选取是软测量技术得以成功应用的基础。通过对丁苯橡胶工艺的深入了解，并与装置技术人员广泛交流，分析影响丁苯橡胶聚合转化率的主要因素，最终确立了与其密切相关的3个辅助变量:即最后一台聚合反应釜出口管道的水平压差p1、釜内垂直压差p0、胶浆温度t1（℃）。数据采集可通过相应的传感器获得，采集点设置如图2所示。

图2 辅助变量采集点示意图Fig 2 Illustration of the acquisition point for secondary variables

图2与文献［3］中类似图的不同之处在于:去除了文献［3］图中的环境温度（该企业当地环境温度影响较小），增加了水平压差p1。

丁苯聚合转化转化率作为预测的目的变量，数据可通过实验室人工化验分析值的记录获得。因此，目的变量预测值与辅助变量间的关系可由下式描述

2.2 预测模型建立与预测结果分析

1）预测模型建立

数据采集与预处理:首先，由上述传感器对3个辅助变量进行数据采集，并获取目的变量人工分析值 ，对辅助变量和目的变量数据应做好时间的匹配。这里采用2009年4，5月份工业现场采集的数据，剔除记录不全和记录异常的，共得到317组数据，使用其中的267组作为训练集，剩余的50组作为测试集。

KPLS建模:先对训练组的3个辅助变量组成的数据矩阵X进行相应的非线性映射，得到核数据矩阵K;然后再对数据阵K和对应的目的变量向量Y做PLS算法，最终得到KPLS模型。

预测:用测试集进行测试。

模型的建立和预测过程如图3所示。

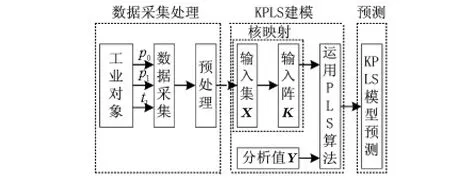
图3 丁苯橡胶聚合转化率KPLS建模过程示意图Fig 3 Illustration of KPLS modeling process for the polymerization conversion rate of SBR

2）预测结果分析

为比较不同核函数引入对PLS建模精度的影响，分别对PLS，poly-KPLS，rbf-KPLS及mix-KPLS四种算法构建的模型进行了仿真，3类核函数形式如下

式中α为可调参数，通过该参数的调解可以配置2种不同性能核函数在混合核中的比重，从而发挥出混合核特有的功能，以更好地适应复杂工况。

KPLS应用过程中涉及到主元个数的确定，核函数类型及其参数的选取，考虑目前尚无统一理论依据。经反复试验，各模型较优状态时的参数设定如表1所示。

由于KPLS经过非线性映射将原空间映射到高维的特征空间，其主元数目会比PLS多，以附有更多的非线性特征信息。

依照上述各模型参数设定，采用测试集对模型泛化性能进行检验。企业要求|^yt－yi|＞的比例（本文命为脱靶率）不大于10%，为了对模型性能做出评价，这里选用预测值与人工分析值之最大绝对误差MAE、均方根误差RMSE和脱靶率等三项指标，算式如下

表1 不同模型参数设置Tab 1 Parameters setting for different models

式中^yt为预测值，yt为化验值，l为测试组数据数目，m为绝对误差大于1.5的个数。各模型测试结果如表2，图4，图5所示。

表2 不同算法下的模型精度Tab 2 Model precisions for different algorithms

图4 mix-KPLS模型预测结果Fig 4 Prediction result of mix-KPLS model

图5 mix-KPLS模型预测误差Fig 5 Prediction error of mix-KPLS model

从表2可以看出:3种KPLS模型均可满足企业对预测精度的要求，而mix-KPLS模型的预测效果更优。

3 结束语

本文以丁苯橡胶生产实例为背景，考虑工况复杂性和PLS较弱的非线性问题处理能力，分别构建了基于单核与混合核的丁苯橡胶聚合转化率PLS预测模型，此类方法融合了“核”的思想和PLS算法数据提取同时考虑自变量和因变量的特点，提高了PLS的非线性处理能力。与常用的其他建模方法相比，基于核的PLS还有着算法简单、易于操作实现等优点。丁苯橡胶聚合转化率建模预测仿真结果表明:此类方法具有较高的预测精度和良好的泛化性能，能满足企业要求聚合转化率预测绝对误差大于1.5的比例不大于样本总数的10%，对丁苯橡胶的平稳高效生产具有一定的指导意义。

［1］刘 美，黄道平，李 桢.丁苯橡胶门尼粘度软测量［J］.自动化仪表，2008，29（12）:33 －34.

［2］刘 美，黄道平，孙宗海.基于PCA和LS-SVM的丁苯橡胶的门尼粘度预测［J］.计算机与应用化学，2008，15（11）:1317－1320.

［3］徐文艳.基于软测量技术的丁苯橡胶聚合率在线监测［J］.化工自动化及仪表，2010，37（10）:124 －126.

［4］李 炜，章 寅，倪 源.基于集成修剪的丁苯橡胶聚合转化率软测量［J］.仪器仪表学报，2011，32（1）:212 －217.

［5］俞金寿.工业过程先进控制技术［M］.上海:华东理工大学出版社，2008，8:83.

［6］Roman R.Kernel partial least squares regression in reproducing kernel hilbert space［J］.Journal of Machine Learning Research，2001，2（6）:97 －123.

［7］Roman R，Nicole K.Overview and recent advances in partial least squares［C］//Lecture Notes in Computer Science，Heidelberg:Springer，2006.

［8］Kim K，Lee J M，Lee I B.A novel multivariate regression approach based on kernel partial least squares with or-thogonal signal correction［J］.Chemometrics and Intelligent Laboratory Systems，2005，79（1 －2）:22 －30.

［9］Jia R D，Mao Z Z，Chang Y Q，et al.Kernel partial robust M-regression as a flexible robust nonlinear modeling technique［J］.Chemometrics and Intelligent Laboratory Systems，2010，100（2）:91－98.

［10］Hiromatsu K，Takahara J，Nishihara T，et al.Prediction for biodegradability of chemicals by kernel partial least squares［J］.Journal of Computer Aided Chemistry，2009，10:1 －9.

［11］Jo J H，Jo E M，Park D，et al.Application of kernel partial least square to predict biological hydrogen production by enterobacter aerogenes［J］.Journal of Nanoelectronics and Optoelectronics，2010，5（2）:203 －207.