一种多传感器信息融合的可能性关联方法*

周新宇，杨风暴，吉琳娜，李香亭

（中北大学信息与通信工程学院，山西太原 030051）

0 引言

多传感器信息融合是对来自多个信息源的不确定信息进行多级别、多方面、多层次的处理，从而产生关于目标更准确、更全面的信息。目标关联建立不同信息源在不同时间、空间所获取目标信息之间的联系，是目标跟踪和态势估计中必不可少的环节。

通常传感器测量过程中存在多种不确定性因素，不确定性通常表现为数据的不完整、不一致及虚假数据。这种不确定性破坏了测量值和目标之间的一一对应关系，导致测量数据与目标对应关系不确定，增加了目标关联的困难。

传统关联方法中，最近邻域法和概率数据关联抗干扰能力差、易产生关联错误;联合概率数据关联（JPDA）及其改进形式，描述的是随机现象，将测量值作为目标的随机事件［1～3］。测量值的不确定性表现为可能性而不是随机性，传统方法不能很好地表达测量值的不确定性，因此，关联错误率较高。

可能性理论是Zadeh A于1978年在模糊集理论的基础上提出来的［4］，是处理不确定信息的一种方法，能够充分地表达测量值的不确定性，在处理不确定性时更符合人类的思维方式。此外，较低的信息量和时间计算复杂度，使其成为信息融合研究的热点。因此，引入可能性分布来表述测量值与目标不确定的关系，将测量数据与目标之间的不确定关系量化为经典的决策问题，为不确定关联问题提供了一种简单而有效的解决方法。

1 可能性理论

1.1 可能性理论的基础

模糊集通过隶属度来描述模糊性，模糊性主要表现为可能性，可能性分布与可能性测度是可能性理论的2个重要概念［5，6］。

设是论域U的一个模糊子集，其隶属度函数为μ~A（u），其中，u∈U，由~A产生的关于u模糊限制记为R（u），命题“u是”把变量u同一个等于R（u）的分布联系起来，该分布记为πu，即可能性分布πu=R（u），反映了变量u不同取值对应命题“u是”的可能性的大小。

定义1:设πu:U→［0，1］满足 sup{πu|u∈U}=1，则称πu为论域U上的可能性分布函数。

定义2:给定论域U上关于变量u的可能性分布函数πu，则的可能性测度为

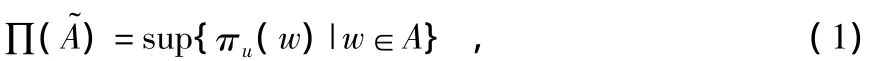
式中 ∏（）表示“中存在某个w作为u的值”的可能性程度，而πu（w）为变量u取值为w的可能性［7］。

1.2 测量数据的可能性表达

在传感器测量中，真值是客观不变的，设真值为x0，定义精确集合:A={x0}，测量值为xj（j=1，2，…，），经典集合用特征函数刻画测量值xj与集合A之间的关系

即xj要么属于A，要么不属于A。由于测量误差和认识的主观性，真值对测量者来说是主观不确定和模糊的，把一个测量值作为真值和非真值都不现实，因此，可把真值处理成一个关于U的模糊集，并赋予一个可能性分布［8］，来描述测量值xj与真值的相容程度π（xj）。

2 可能性分布关联模型的建立

2.1 目标特征的统计距离

通常关联的信息主要为目标状态信息，位置特征是主要的状态信息（经度、纬度）、速度、方向和加速度也是关联的重要特征。

X=（x1，x2，…，xm）表示当前已知的目标集合，Y=（y1，y2，…，yn）为有效测量集合，假设目标和测量值具有s个特征，关联是把当前测量值分配给已知目标，多目标关联可以分解为测量值yj（j=1，2，…，n）与目标xi（i=1，2，…，m）的多目标决策问题。

（k|k－1）表示目标xi在第k时刻位置的预测，Dk（i，j）表示目标xi与测量值yi在k时刻的统计距离

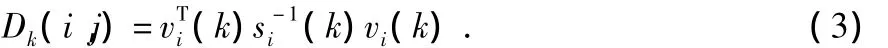
其中，vi（k）=Zi（k）－Zi（k|k－1）表示新息，si（k）为新息协方差。

其他特征的统计距离Dk（i，j）等于k时刻第j个测量值yi同第i个目标xi的预测值关于该特征的分量之差

其中，xit和yjt分别表示目标xi和测量值yj的第t（t=1，2，…，s）个特征分量。

2.2 基于目标特征的可能性分布

测量值yj与目标xi在k时刻关于某特征的统计距离Dk（i，j）表征二者在该特征上的相关性，Dk（i，j）越大，相关程度越小，反之，相关程度越大。通过Dk（i，j）构造测量值yj关于目标集X在特征分量上的可能性分布，由Dk（i，j）与相关程度可知，为偏小型可能性分布［9］。位置特征（经度、纬度）、速度、加速度和方向的可能性是关于Dk（i，j）的减函数，但关于Dk（i，j）的变化不同，它们的可能性分布并不完全相同。

对于位置、速度和方向，当Dk（i，j）≤a时，可能性近似为 1，当a≤Dk（i，j）≤b时，可能性对Dk（i，j）变化敏感度不大，b≤Dk（i，j）≤c时，敏感度增大，上述特征近似服从Z型分布，函数关系如下

a为可能性为1时，Dk（i，j）的最大阈值，通常很小，当然由于特征量纲，不同特征对应的a并不相同;b为可能性过渡点，当Dk（i，j）=b时可能性为0.5，测量值yj与目标xi在对应特征的关联模糊性最大，是可能性变化的拐点;c为可能性为0时，Dk（i，j）的最小阈值，c值通常较大。

加速度表征目标的机动性，在相邻的采样周期内，通常变化不大，运动中不同于其他特征，可能性分布近似服从k次抛物线分布，函数关系如下

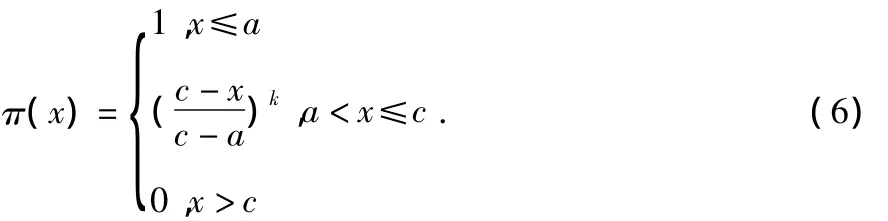
当Dk（i，j）＞a时，可能性对Dk（i，j）变化很敏感，其减小速度较快，而后随着D（i，j）增大，可能性变化率减小，减小速度放缓。

2.3 变权可能性算子

测量值yj关于目标xi在特征分量t（t=1，2，…，s）上的可能性为（t），且满足0≤（t）≤1（t）表示测量值yj与目标xi在特征t上的关联支持度，求得测量值yj与X中目标在特征t上的可能性，得到特征t的可能性分布。

综合s个特征，测量值yj与目标xi的综合可能性

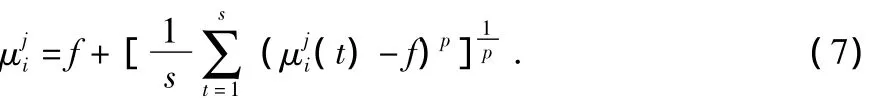
其中，f=0.5，p为奇整数，决定各特征在关联决策中的权值，p较小时，模糊度较高的特征对关联结果影响较大，反之，模糊度较高的特征对关联的影响较小，因此，p的选取较为重要。p=1时为算术平均值;p≥3时，高模糊度的特征对关联的综合评价有很小的影响;当p→∞时，特征分量中的最大可能性的作为最终的关联可能性。

2.4 关联判断

可能性关联模型建立分以下几个步骤:

1）各特征分量的统计距离确定:应该根据式（3）或者式（4）计算测量值yj与目标xi在各特征分量上的统计距离;

2）特征差异模糊化:利用可能性分布函数式（5）或式（6），计算测量值yj与目标xi在各特征分量上关联可能性（t）大小;

3）关联综合评价:通过变权可能性算子式（7）计算测量值yj与目标xi的综合关联可能性。4）关联决策:由（i=1，2，…，m），选取可能性最大的目标xt，即

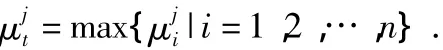
当＜0.5（选取p=3）时，支持关联成功的可能性小于关联失败的可能性，xt不能作为关联目标;=0.5 时，关联的模糊性最大，也不能判断yj与xt关联与否，将测量值yj当作新目标;当＞0.5时，确定xt为yj的关联目标。

3 仿真分析

假设3个目标交叉运动的仿真场景，随机分布的杂波密度为0.3/km2，传感器采样周期T=4 s，采用拓展卡尔曼滤波器（EKF）对目标状态进行估计和预测，只考虑目标在二维平面（X—Y）的运动，用传统的JPDA和可能性方法进行比较，蒙特—卡洛仿真次数为100次，仿真结果如图1～图5所示。图1为3个目标在空中的运动情况，符号o表示随机分布的杂波。图2表示传统JPDA的关联情况，当目标1与目标3运动到同一区域时，即目标交叉或接近时，JPDA不能正确进行关联和跟踪;图3为可能性方法的关联运动过程，3个目标均能进行准确的关联和跟踪，因此，可能性关联方法正确率明显高于JPDA。

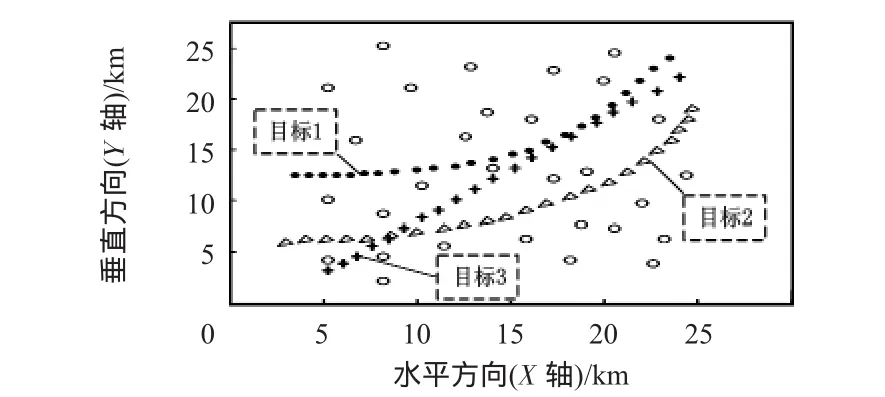
图1 目标的运动过程Fig 1 Moving process of targets

图4、图5分别采用JPDA（用符号o表示）和可能性方法（用符号+表示）时，目标2在X方向和Y方向上的均方误差（RMSE），可能性方法关联精度明显高于传统的JPDA。

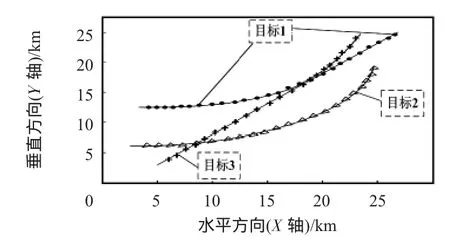
图2 JPDA目标关联运动过程Fig 2 Target association moving process of JPDA

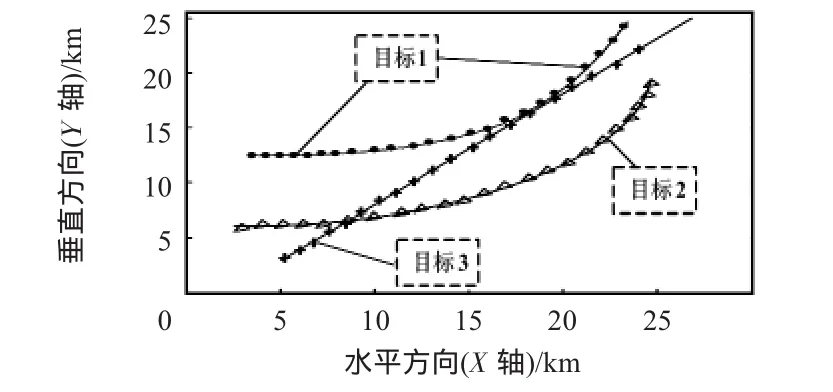
图3 可能性方法目标关联运动过程Fig 3 Target association moving process of possibility method

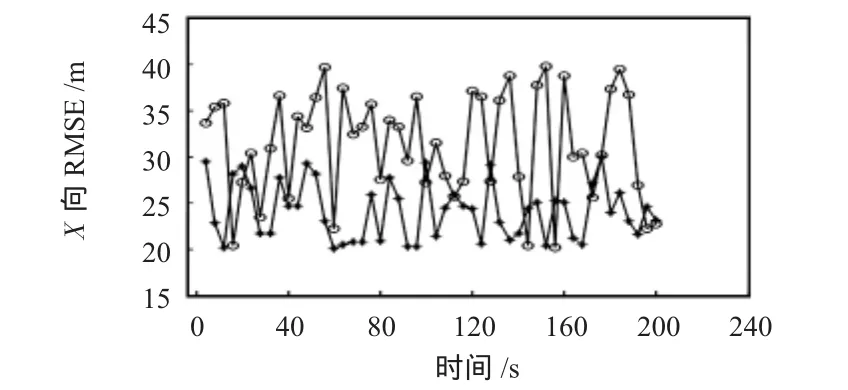
图4 目标2的X方向均方误差Fig 4 RMSE of X direction of target 2

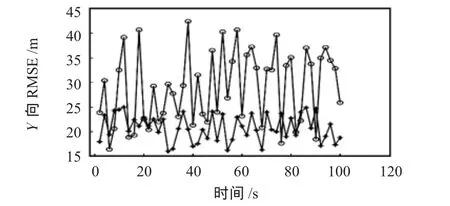
图5 目标2的Y方向均方误差Fig 5 RMSE of Y direction of target 2

4 结束语

传感器的测量值天然地具有多种不确定性，传统方法不能很好地表达这种不确定性，而可能性理论能充分地描述测量值的不完备状态。引入可能性理论建立了一种可能性关联模型，将测量值与目标在特征分量上的统计距离进行模糊化，构造了测量值关于目标的可能性分布，很好地反映测量值与目标真值的相容程度，并通过可能性分布量化这种模糊关系，并得到客观的关联结果。

［1］何 友，王国宏，关 欣，等.信息融合理论及应用［M］.北京:电子工业出版社，2010，194 －202.

［2］周新宇，杨风暴，吉琳娜.一种新的地面目标多特征关联方法［J］.通信技术，2011，44（9）:132 －134.

［3］万树平.运用Vague集进行多传感器目标识别［J］.传感器与微系统，2011，30（1）:58 －78.

［4］Zadeh L A.Fuzzy sets as a basis for a theory of possibility［J］.Fuzzy Sets and Systems，1978，1（1）:3 －28.

［5］Silva R C，Yamakami A.The use of possible theory in the definition of fuzzy pareto-optimality［J］.Fuzzy Optim Decis Making，2011，3（10）:11 －30.

［6］Peng Yi，Kou Gang，Wang Guoxun，et al.FAMCDM:A fusion approach of MCDM methods to rank multiclass classification algorithms［J］.Omega，2010，10（10）:1016 －1028.

［7］Lohweg V，Voth K，Glock S.A possibilistic framework for sensor fusion with monitoring of sensor reliability［J］.Sensor Fusion-Foundation and Applications，2011，32（4）:191 －226.

［8］肖明珠.基于可能性理论的测量数据处理［J］.信息与电子工程，2006，4（2）:98 －102.

［9］胡宝清.模糊理论基础［M］.武汉:武汉大学出版社，2010:473－517.