基于抽取与重构的瞬时频率估计算法*
2012-07-25司伟建
司伟建,蒋 鹏
(哈尔滨工程大学信息与通信工程学院,黑龙江哈尔滨 150001)
0 引言
瞬时频率(instantaneous frequency,IF)是描述信号时变特征的基本参数,广泛应用于工程应用领域,如地震、雷达、通信领域的信号识别、跟踪估计等。
瞬时频率的定义最早是由 Carson J R 与 Fry T C[1~3]提出,Ville将Gabor提出的解析信号与Carson及Fry的工作结合起来将瞬时频率定义为解析信号的相位导数。Ville提到,由于瞬时频率是时变的,所以,应该存在有与瞬时频率相对应的瞬时谱,并且该瞬时谱的平均频率即为瞬时频率[4~6]。利用 Gabor的平均测度,Ville证明了信号谱的平均频率等于瞬时频率的时间平均。但是Ville并没有进一步推导与瞬时频率相对应的瞬时谱的表达式或者瞬时频率的概率密度分布[7,8]。
本文从瞬时频率的定义出发,研究了AWGN信道中采样信号的瞬时频率的概率密度分布。在差分运算的基础上,提出了一种基于抽取与重构的瞬时频率的估计算法,该算法具有与差分运算相似的瞬时频率概率密度分布,根据分布模型的参数可知,该算法能够极大地提高单载波信号瞬时频率的估计性能。对于多载波信号,该算法同样能够提高瞬时频率的估计性能,但是在提高估计性能的同时存在错误的瞬时频率现象,本文称其为虚假瞬时频率(spurious IF)。如果在后续的处理中能够剔除这些虚假瞬时频率,那么对于提高多载波信号瞬时频率的估计性能是非常有利的[9~11]。
1 瞬时频率的概率密度分布
在方向数据统计理论中Von Mises分布M(μ0,k)在圆上分布中占有重要的作用,其密度函数为
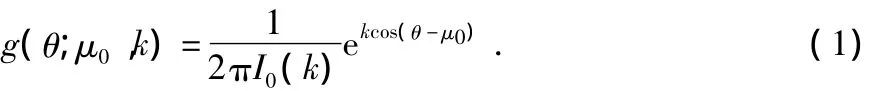
其中,I0(·)为修正的第一类零阶Bessel函数
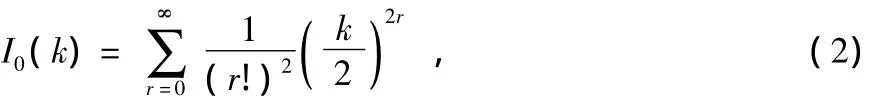
且式(1)μ0中和k的取值有如下约定:
依余弦函数的性质,有M(μ0+π,k)=M(μ0-k),为克服由此带来的不确定性,约定0≤μ0<2π,k>0。
本文提出了载波信号差分运算得到的瞬时频率分布服从Von Mises分布的假设,且该分布的参数与载波频率,采样频率和信噪比有关,表达式如式(3)和式(4)所示

式中fc为载波信号频率,fs为信号的采样频率。ρ为信噪比,S为信号功率,N0为噪声功率。文中在第3.2部分给出了假设检验结果。一般而言,信号的采样频率应满足Nyquist采样定理,即采样频率不低于信号最高频率的2倍,因此,式(3)总能满足μ0在[0,2π)区间或者[-π,π)区间。
对于MFSK这类多载波信号而言,瞬时频率的分布是关于2πfc/fs对称的多峰分布。其中每一个峰均符合Von Mises分布,相应的μi=2π(fc±nΔF)/fs,其中,ΔF为载波频率间隔,n=(2(m-1)/2;m为调制阶数。
图1给出不同采样频率和不同信噪比下FSK信号载波频率的概率密度分布曲线。载波信号的中心频率经下变频后fc=0,同时令κ=ΔF/fs为归一化频偏。图1(a)为在信噪比ρ=10时,不同的归一化频偏时的概率密度分布曲线。图1(b)为在归一化频偏为κ=0.075时,不同信噪比下的瞬时频率的概率密度分布曲线。根据前面的分析可知,FSK信号的瞬时频率分布的峰间距为Δμ=4πκ,当两峰尖之间的峰谷值大于等于峰尖值时,那么FSK信号的2个瞬时频率就会完全混叠在一起,以至于无法分辨。
从图1(a)中可知,当信噪比ρ一定时,κ≤κT时,FSK信号的2个瞬时频率无法分辨。为了能够分辨2个瞬时频率,归一化频偏κ应大于κT

当信号的频偏一定和信噪比ρ一定时,fs≥fT时,FSK信号的2个瞬时频率无法分辨。为了能够分辨2个瞬时频率,采样频率fs应小于fT,但同时fs不能小于信号最高频率的2倍,以满足Nyquist采样定理


图1 κ,ρ不同时FSK信号载波频率的概率密度分布曲线Fig 1 Curve of probability density distribution of FSK carrier signal frequency under different κ and ρ
从图1(b)中可知,对于FSK信号而言,归一化频偏κ一定时,当信噪比恶化时,2个瞬时频率将部分混叠在一起,而当信噪比在ρ≤ρT时,FSK信号的2个瞬时频率将无法分辨。因此,为了能够分辨2个瞬时频率,信噪比ρ应大于ρT

2 瞬时频率的估计算法
对于单载波信号,改变信号的采样频率只会改变瞬时频率概率密度分布的位置,并不会改变瞬时频率概率密度分布的尺度。而对于多载波信号,只要瞬时频率不发生混叠,改变信号的采样频率也只改变各个峰分布的相对位置,不会改变分布的尺度。根据这个结论,本文提出了一种基于抽取与重构的瞬时频率估计算法,并且从理论上分析了该算法对瞬时频率概率密度分布的影响,以及该算法对载波信号瞬时频率估计的性能。
算法描述:对原始采样序列x(n)以整数倍D进行抽取,以形成一个新序列xD(m)使抽取后的抽取序列取样率fs/D不小于载波信号最高频率的2倍以满足Nyquist采样定理。根据取样的不同起始时刻可以得到D个序列xD(m),xD(m+1),…,xD(m+D-1),对每个序列分别求取瞬时频率序列fif(m),fif(m+1),…,fif(m+D-1),对瞬时频率重构后除以抽取倍数D,即可算得采样频率fs下的瞬时频率。现分析该算法的瞬时频率分布情况。
从算法的描述中可知瞬时频率依然服从Von Mises分布,但是分布的参数相应的变为如下表达式

从公式(9)可知,该算法比直接用差分法求瞬时频率时信噪比提高了D2倍。该算法对于提高单一载波信号的瞬时频率的估计精度具有良好的效果,但是对于频率不是恒定的信号(如FSK信号),这种算法在提高估计精度的同时会引入虚假的瞬时频率。原因是当FSK信号频率改变时,信号的瞬时相位变化曲线(理论上该变化曲线是一条直线)就会改变,将原始采样信号以整数倍D进行抽取后,对于相隔D点的2个相位有可能正好位于2个变化曲线上,差分运算后就会产生虚假的瞬时频率。当信号的采样速率远大于码元速率且D较小,该算法所产生的虚假瞬时频率对瞬时频率的分布和瞬时频率的判断并无多大影响,但当采样频率不够高而抽取的D较大,或者信号的瞬时频率变化较快时,这种虚假瞬时频率的影响也许会导致错误的结论。
综合以上分析,对于不同的载波信号应采取不同的策略,对于单载波信号应尽可能地选取较大的抽取倍数以提高估计精度,而对于多载波的信号,应根据不同的应用场合选取合适的抽取倍数。
3 蒙特—卡罗模拟实验
3.1 分布模拟
为了分析瞬时频率计算方法对瞬时频率概率分布的影响,分别对单载波信号和多载波信号进行了仿真分析。图2(a)对单一载波信号的瞬时频率分别采用差分运算和本文提出基于抽取与重构的算法进行计算机仿真(图中D=1即为差分运算方法),并且将仿真结果与各自的理论分布曲线画在同一个图上,以方便分析和比较。图中归一化频率κ=1/15,信噪比ρ=10。差分运算(D=1)的瞬时频率分布与M(2π/15,10)的 Von Mises分布相一致,本文提出的算法当D=3时的瞬时频率分布与M(2π/15,90)的Von Mises分布相一致。图2(b)对多载波信号(FSK)的瞬时频率分别采用差分运算和本文提出的算法进行计算机仿真,将仿真结果与各自的理论分布曲线同时画在同一个图上。图中归一化频率,信噪比ρ=20约13 dB。从图中可以明显地看出:当以2倍抽取(D=2)时,在O点附近产生了虚假瞬时频率,当两瞬时频率的分布曲线跟虚假的瞬时频率没有重叠时,是能够将该虚假频率从真实的频率中剔除出去,这样就能提高瞬时频率的估计精度。
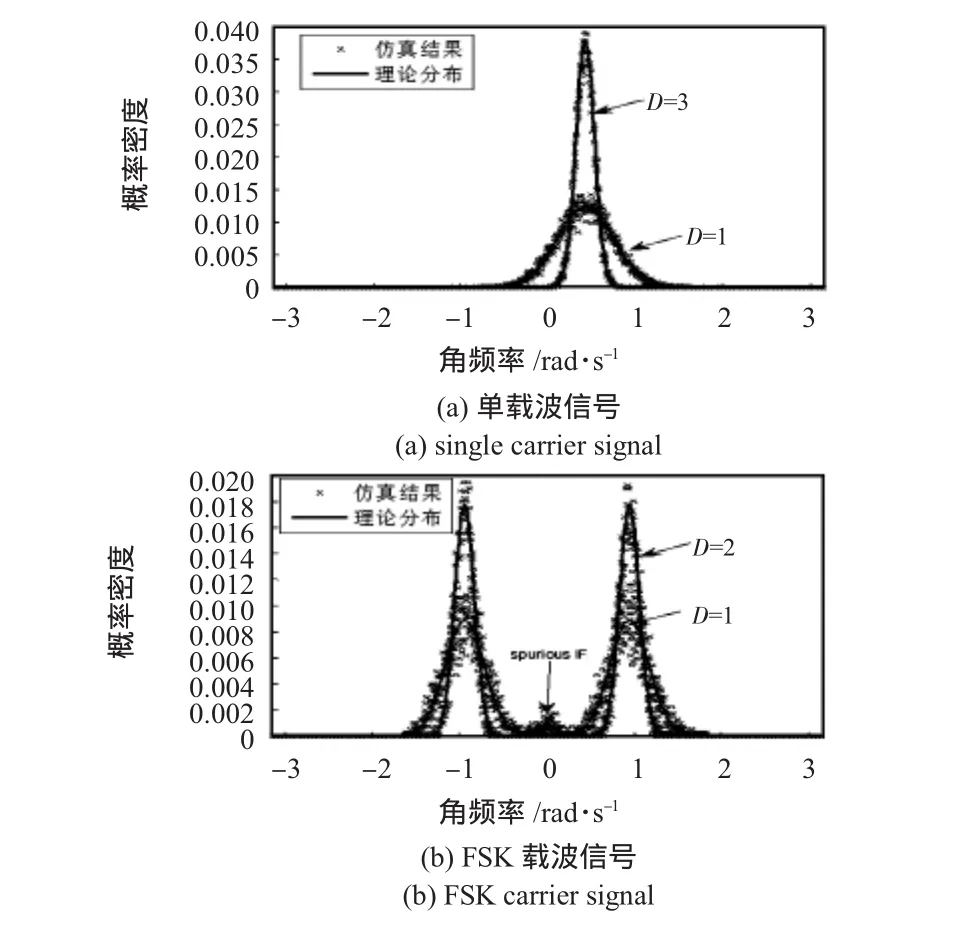
图2 不同的抽取值D对单载波信号和FSK载波信号瞬时频率分布的影响Fig 2 Effect of different value of D on single carrier signal and the FSK carrier signal instantaneous frequency distribution
3.2 假设检验计算

表1 瞬时频率概率分布的拟合优度检验Tab 1 Goodness-of-fit test of instantaneous frequency probability distribution
4 结论
本文提出了在AWGN信道中载波信号采样序列的瞬时频率的概率密度分布模型,并且通过假设检验的方法验证了该假设,给出了假设检验结果。同时根据该分布模型提出了一种提高瞬时频率估计精度的算法。从仿真结果可以看出:在低信噪比的情况下,该算法仍能保持96%以上的正确率。文中还分析了多载波信号采样序列的瞬时频率产生混叠以至无法分辨的情况,推导了瞬时频率完全混叠时的极限公式,并且详细分析了虚假瞬时频率产生原因。如果在后续的处理中能够剔除这些虚假瞬时频率,那么对于提高多载波信号瞬时频率的估计性能也是非常有利的。
[1]Carson J R,Fry T C.Variable frequency electric circuit theory with application to the theory of frequency modulation[J].Bell Sys Tech,1937,16(1):513 -540.
[2]Boashash B.Estimating and interpreting the instantaneous frequency of a signal-part 1:Fundamentals[J].Proceedings of the IEEE,1992,80(4):520 -538.
[3]Boashash B.Estimating and interpreting the instantaneous frequency of a signal-part 2:Algorithms and applications[J].Proceedings of the IEEE,1992,80(4):540 -568.
[4]王竹溪,郭敦仁.特殊函数概论[M].北京:北京大学出版社,2004.
[5]Dacidson K L,Cazzanti L,Pitton J W.Feature-based modulation classification using circular statistics[C]//2004 IEEE Military Communication Conference,2004:765 -771.
[6]李元生.方向数据统计[M].北京:中国科学技术出版社,1998.
[7]杨小牛,楼才义,徐建良.软件无线电原理与应用[M].北京:电子工业出版社,2001.
[8]刘庆云,陆飞飞,朱伟强.辐射源细微特征用于个体识别的可行性分析[J].航天电子对抗,2008(2):40-42.
[9]Abdi A,Bargnr J A,Kaveh M.A paranaetric model for the distribution of the angle of arrival and the associated correlation function and power spectrum at the mobile station[J].IEEE Tram VT,2002,51(3):425 -434.
[10]许月一.辐射源指纹机理及识别方法研究[D].长沙:国防科学技术大学,2008.
[11]朱力行,许王莉.非参数蒙特—卡罗检验及其应用[M].北京:科学出版社,2008.
