磁浮寻北仪转位误差对寻北精度的影响分析*

2012-07-25仲启媛黄先祥谭立龙

传感器与微系统 2012年3期

仲启媛，黄先祥，谭立龙

（第二炮兵工程大学202教研室，陕西西安 710025）

0 引言

陀螺寻北仪的悬挂方式有吊带式和磁悬浮式，目前广泛应用的悬挂方式是吊带式，它结构简单，整机重量轻，寻北精度高，但吊带式陀螺寻北仪运动周期长，使得其定向速度较慢，不能满足快速定向的要求。而磁悬浮悬挂方式是一种无磨擦、无磨损的悬挂方式，用它支承陀螺敏感元件，可以消除轴承摩擦对陀螺盘房体运动的影响，它将测量敏感元件的周期摆动测北改为测量指北反馈力矩测北，使寻北时间大为缩短，从而实现快速而精确的寻北［1］。

1 磁悬浮陀螺寻北仪的寻北原理

磁悬浮陀螺寻北仪结构原理示意图如图1所示，主要由陀螺敏感元件、陀螺电机稳速控制系统、磁悬浮控制系统、力矩反馈控制系统、A/D采样系统、随动壳体驱动系统、高精度测角系统等组成。

当陀螺马达经电机稳速控制系统启动至规定转速并稳速后，给磁悬浮线圈通电，敏感元件顶部的球头衔铁受到磁力吸引，带动敏感元件向上运动，位置传感器感知其上浮的位置，经磁浮控制电路控制磁悬浮线圈中的电流，构成磁悬浮反馈系统，最终使敏感元件所受磁悬吸力与重力平衡，并悬浮于平衡位置。敏感元件悬浮后，受地球自转影响而产生进动，进动力矩与陀螺主轴和北向夹角的正弦值成比例。通过敏感元件下方的力矩阻尼器施加与陀螺力矩反向的阻尼力矩，并由光学传感器感知陀螺主轴的位置，经力矩反馈控制电路改变力矩阻尼器电流的大小，从而使陀螺主轴指向随动壳体参考位置不动，然后通过A/D采样检测力矩阻尼电流大小，间接解算出陀螺主轴与子午面的夹角。随动壳体可由随动壳体驱动机构带动相对外层壳体可以旋转，随动壳体参考位置与外层壳体最终的参考基准方向之间的夹角可由高精度测角系统给出，这样可最终计算外层壳体上参考基准方向的方位角［2］。

2 相关的坐标系介绍

2.1 地理坐标系 onxnynzn［3］

图1 磁浮陀螺寻北仪结构原理示意图Fig 1 Principle diagram of magnetic suspension gyro north-seeking’s structure

地理坐标系取为“东、北、天”坐标系，即原点on位于寻北仪架设所在的点;xn轴沿当地纬线指东，yn轴沿当地子午线指北，zn轴沿当地地理垂线指上并与xn，yn轴构成右手直角坐标系。其中，xn轴与yn轴构成的平面即为当地水平面，yn轴与zn轴构成的平面即为当地子午面，所谓“寻北”即是确定子午面位置，如图2所示。

2.2 载体坐标系 obxbybzb［4］

载体坐标系的原点取在敏感元件的悬挂中心;zb轴为陀螺寻北仪纵轴，指向上方为正;yb轴平行于测角系统零位方向;xb轴与yb，zb轴构成右手直角坐标系，如图3所示。当仪器精确调平时，载体坐标系的xbobyb平面与当地水平面平行，载体坐标系随着壳体的变化而变化。

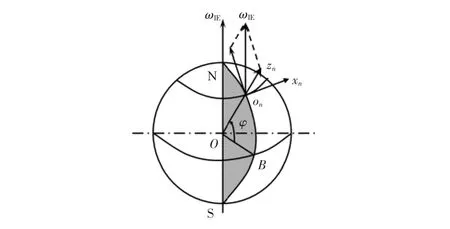
图2 地理坐标系onxnynznFig 2 Geography coordinate onxnynzn

设载体参考方向的方位角为α，由方位角定义（以正北为起始方向，顺时针转至参考方向）可知，α以绕zb负方向旋转为正。载体没有调平时，绕xb轴旋转产生的角度为纵倾角（即俯仰角），记作θ，绕yb轴旋转产生的角度为横倾角（即横滚角），记作γ，正负号规定为:产生倾角的旋转方向与坐标轴指向相同时，为正，否则，取负，即参考方向朝北时，载体北高南低纵倾角θ为正，西高东低横倾角γ为正。则由地理坐标系onxnynzn到载体坐标系obxbybzb的转换关系Cbn表示为

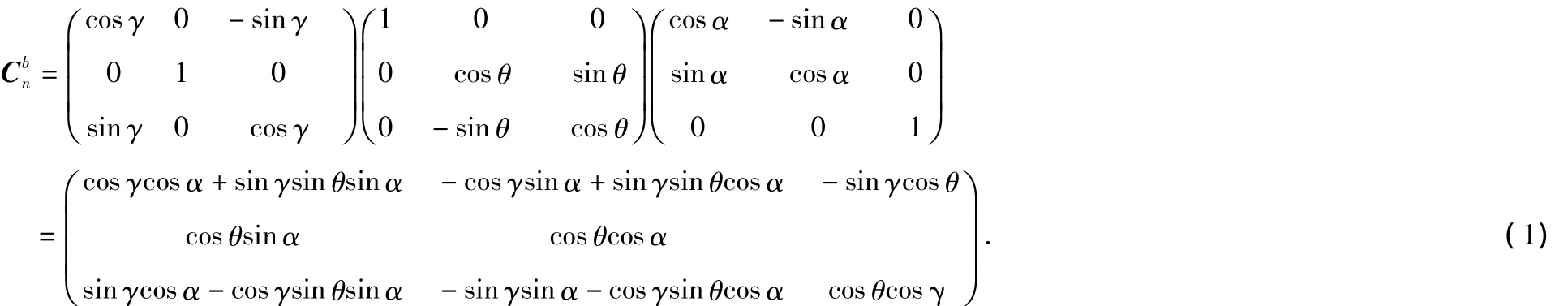
在使用时，仪器一般情况下是精确调平的，即载体坐标系的xbobyb平面与当地水平面平行，即载体坐标系的xb，yb轴均在水平面内，γ和θ为0。

2.3 陀螺坐标系ogxgygzg

陀螺仪在惯性空间的运动用陀螺坐标系的运动角速度变化来描述。陀螺坐标系的原点og取在敏感元件的悬挂中心;yg轴与陀螺自转轴重合，方向指向角动量方向;zg轴是转子中心与回转中心连线方向，指向上方为正;xg轴平行于赤道平面并与yg，zg轴构成右手直角坐标系，如图3所示，陀螺坐标系随着陀螺仪的运动而变化。

由于陀螺灵敏部上部受球头衔铁与底部磁悬浮轴承的限制，在寻北过程中，受到力矩器施加的阻尼力矩的驱动，陀螺坐标系ogxgygzg只相对载体坐标系obxbybzb的zb转动，且通过力矩反馈电路尽可能使yg轴指向光学传感器准直零位，假设陀螺坐标系ogxgygzg相对载体坐标系obxbybzb的转角为A，以绕zb负方向转动为正，则由载体坐标系obxbybzb到陀螺坐标系ogxgygzg的坐标变换矩阵为

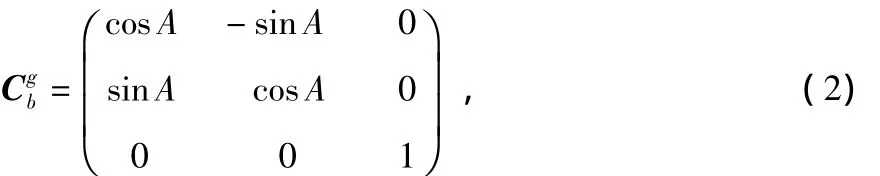
则在陀螺坐标系中地球自转角速率分量为［3］

其中，ωie为地球自转角速度，φ为陀螺架设点的纬度。

图3 载体坐标系与陀螺坐标系Fig 3 shell reference frame and gyro reference frame

3 转动机构转位误差对寻北精度的影响

磁悬浮陀螺寻北仪在精寻北时，在相差180°的2个位置上寻北，在第一位置对敏感器件输出采样完成后，由转动机构带动陀螺组件旋转180°，再次进行测量，这样可以抵消陀螺常值漂移的影响，提高寻北精度［5］。而在由第一位置转到第二位置时，如果没有精确地转动180°，转动结构的转位误差会给寻北带来一定的误差。

在第一位置，即陀螺坐标系ogxgygzg相对载体坐标系obxbybzb的zb轴转角A=0，根据式（2），此时载体坐标系obxbybzb到陀螺坐标系ogxgygzg的坐标变换矩阵为

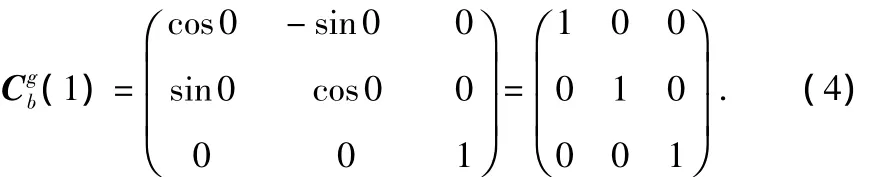
将（1）和公式（1）中的代入公式（3）可求出第一位置陀螺坐标系xg轴和yg轴上的输出为

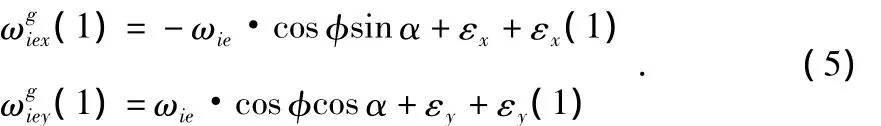
在第一位置对敏感器件输出采样完成后，由转动机构带动陀螺组件旋转180°至第二位置，如果没有精确地旋转180°，存在转位误差 Δψ，多转为正，少转为负，即A=180°+Δψ，则公式（2）变为［6］

在第二位置，陀螺坐标系x，y轴敏感到的地球自转分量为

其中，Δψ为转动机构转位误差，εx（2），εy（2）为陀螺坐标系x轴和y轴在第二位置的随机漂移。根据公式（5）和式（7），陀螺在两位置的输出为

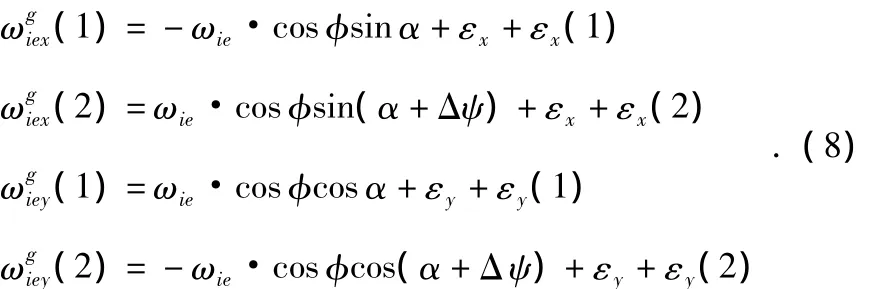
假设忽略随机漂移误差εx（1），εy（1）和εx（2），εy（2），由转动机构的转位误差Δψ引起的寻北误差记为Δαψ，根据公式（8）有

所以，有

由式（10）可以看出

公式（11）表明:由转动机构转位误差Δψ所引起的寻北误差Δαψ是转位误差的一半。这说明，如果转位误差为20″，则由它引起的寻北误差就是10″。所以，提高转动机构转动位置的测量精度，并对转位误差进行精确补偿，可以提高寻北仪的寻北精度［7］，这也是需要进一步研究的内容。为了比对存在转位误差前后陀螺输出信号的变化，首先将陀螺寻北仪架设在实验室的隔振基座上，在基座精确调平，无转位误差和准直误差，并且周围扰动比较小的情况下对基准棱镜进行准直测北，测得陀螺输出信号10组数据，采样时间为10ms，每组采样数据为1000个，取其中的任意一组，如图4（a）所示，陀螺输出数据有微小波动，主要是由于电路白噪声引起的，该组信号的标准方差为2.496 8×10－5。

还是将寻北仪架设在隔振基座上对基准棱镜进行准直测北，当存在转位误差30″时，测得陀螺输出信号10组数据，采样时间为10 ms，每组采样数据为1000个，取其中的任意一组，如图4（b）所示，发现陀螺输出数据有较大波动，该组信号的标准方差为7.6484×10－5，存在转位误差时的标准差是无转位误差时的近3倍。显然，转位误差会影响陀螺的输出，进而影响寻北精度。

在无误差的理想情况下，寻北计算的公式为

式中id（1），iz（1）和id（2），iz（2）分别为在第一位置和第二位置时对力矩阻尼器定转子工作电流的采样值，K为陀螺寻北仪的定向系数，是与力矩器的力矩系数、陀螺动量矩Hg和采样电路放大倍数有关的常数。

图4 无转位误差和存在转位误差时陀螺输出信号的对比Fig 4 Comparison of gyroscope output signals under no position transformation error and existing position transformation error

已知基座棱镜的方位角为1280527.2″，在无转位误差的理想情况下，利用采样数据，根据寻北公式计算棱镜的方位角为1280524.5″，微小误差 2.7″是由电路白噪声引起的。在存在转位误差30″的情况下，如果不进行补偿，直接利用公式（12）计算得到的方位角为1 280 504.5″，误差为22.7″，如果将测得的转位误差角30″带入公式（11），计算出寻北误差再进行补偿，则方位角为1 280 519.5″，误差为7.7″。

表1是对基座棱镜进行5次寻北测量，在存在转位误差时，补偿前后的数据对比。

4 结论

在研究转位误差所引起的寻北误差和相应的补偿措施时，提高测角的精确度是转位误差补偿的前提。此外，由于陀螺的输出会受到许多因素的影响，如基座的水平度，车辆、大风及人员走动所引起的基座扰动，环境温度的剧烈变化等，因此，首先要对陀螺的输出信号进行适当的滤波处理，减小外界的干扰，只有这样才能真正减小寻北误差，提高寻北精度。