综合孔径辐射计可见度函数预处理算法及时域仿真研究

李慧玲 刘 浩 吴 季 牛立杰 张 成

①(中国科学院微波遥感技术重点实验室，中国科学院空间科学与应用研究中心 北京 100190)

②(中国科学院研究生院 北京 100049)

1 引言

干涉式综合孔径技术实现地球静止轨道的微波大气探测成为近年的研究热点，其中包括美国的Geo STAR[1]、欧空局的GAS[2]。为支持微波系列在风云四号静止轨道气象卫星上的实施，中国科学院空间科学与应用研究中心开展了对“地球静止轨道毫米波大气温度探测仪”的项目研究[3-5]。本文以该项目为依托进行综合孔径辐射计可见度函数预处理算法的研究。

综合孔径辐射计的数据处理过程包括两步：首先由数字相关器的原始输出得到可见度函数，然后再由可见度函数反演为亮温分布。本文所做的工作主要针对第1步，即将三阶量化数字相关器的原始输出处理为可直接用于图像反演的可见度函数。

三阶量化数字相关器之前在射电天文学中得以应用，而目前在对地观测领域内，三阶量化数字相关结果的校正算法是首次应用。早期综合孔径辐射计采用的是模拟复相关器，为了达到星载综合孔径辐射计对功耗、重量等指标的要求，数字相关器得以应用。目前国际上综合孔径辐射计系统大多采用1 bit二阶量化数字相关器(如SMOS及GeoSTAR地面样机[6,7])，对应的处理方法较为成熟并已获得实际验证。在相同的精度下三阶量化比二阶量化所需的积分时间更少，灵敏度更高。本文所做工作针对三阶量化数字相关结果进行了定量化的分析。

从仿真手段来看，由于综合孔径辐射计系统复杂度高，目前综合孔径辐射计的仿真均是在空间频率域和空间域所作的基于傅里叶关系的系统仿真，如SMOS的系统仿真软件SEPS等[8]。然而辐射计本身进行的是随机噪声的测量，这种仿真有局限性，特别是无法对量化过程进行仿真，也无法对辐射灵敏度、辐射测量精度等指标进行分析。对综合孔径辐射计的基本构成单元二元干涉仪进行时域的蒙特卡罗仿真，可对构成系统的组件进行误差分析。

本文首先给出了可见度函数预处理的校正算法，然后利用 MATLAB建立了一个对二元干涉仪进行时域蒙特卡罗仿真的平台，特别利用该平台研究了三阶量化对相关性的影响，并验证了可见度函数预处理的校正算法。最后将该算法应用于“地球同步轨道毫米波大气温度探测仪”系统的实验数据处理，并与仿真结果进行对比，验证了该算法的准确性。

2 综合孔径辐射计的误差模型

综合孔径辐射计的基本单元是二元干涉仪，综合孔径辐射计测量的主要目的是通过复相关运算，获得两个接收天线的干涉输出，也就是一个可见度函数的采样值。由数字相关输出得到可见度函数为[9]

其中(u,v)=(Dx/λ0,Dy/λ0)为两天线单元以波长为单位的距离向量，D为天线的方向性系数，F(ξ,η)为归一化的天线复电压方向图，(ξ,η)=(sinθcosφ,sinθsinφ)为入射电磁波的方向余弦，TB(ξ,η)为地物及目标的辐射亮温，为 fringe-washing函数。由于实际天线、接收机与相关器的不理想性导致测量的输出信号相关性相对于输入信号的相关性有所改变，为了校正该误差，其可见度函数预处理过程的框图如图1所示。

图1 可见度函数预处理流程

本文的校正算法主要包括：A/D偏置校正，三阶数字相关至模拟相关值的校正，IQ非理想特性校正，fringe-washing函数校正。校正后得到的模拟相关系数可用于亮温反演算法。

2.1 AD偏置校正

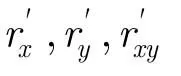
2.2 三阶数字相关至模拟相关值的校正

三阶数字相关器与高阶数字相关器相比易于实现，并且与1 bit的数字相关器相比，在相同的精度下需要的积分时间更少，对于高采样率的信号，三阶量化技术有着很多的优点，所以在本系统中应用三阶数字相关器。三阶量化函数如式(3)所示。此处只讨论c=-a的情况。

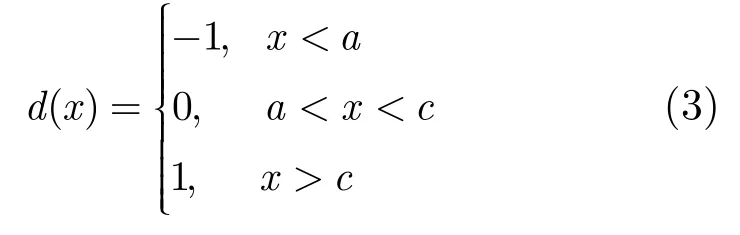
复相关输出结果与量化阈值有密切关系，所以数字相关结果需要修正。为了校正该误差，寻求数字相关与模拟相关之间的关系，文献[10]给出其关系公式如式(4)所示。

其中r11为数字相关系数，ρ为模拟相关系数。v0为量化阈值，σ为输入信号的均方根。当v0/σ=0.6120时为最佳阈值。该积分公式是在模拟相关系数已知的情况下计算三阶数字相关。但是实际应用中，希望通过数字相关来寻求模拟相关结果。文献[11]给出了从数字相关到模拟相关之间的关系的估计算法[11]。文献[11]将积分公式进行泰勒级数展开，取前两项得到该估计算法。如果将积分公式的泰勒展开取到五级幂级数项，可获得更高的精度[12]。

其中

2.3 IQ非理想特性校正

信号的相位是一个非常重要的参数，理想的IQ信号是正交的。但由于IQ双通道存在幅相不平衡或物理器件的不理想性，产生非正交误差。采用IQ自相关校正方法[13,14]校正该误差。同一通道的IQ相关系数rIQ如式(6)所示。

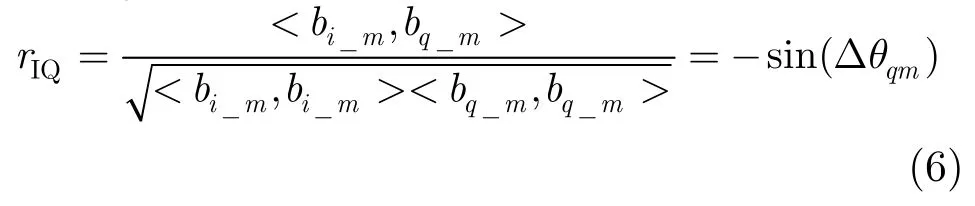
复相关校正公式为

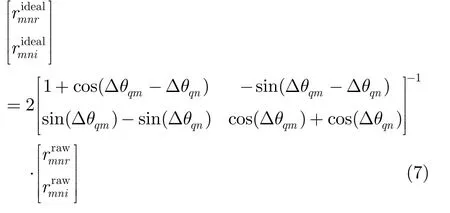
2.4 fringe-washing函数校正

当信号在到达最长基线的延时大到与信号的相关时间(也就是 1/B)具有可比性时，fringe-washing函数对结果产生影响。若接收机频率响应为矩形函数，并且所有接收机频率响应一致，则 fringewashing函数为：rij(τ)=s inc(Bτ)。然而实际上接收机的频率响应不可能完全一致，也不是理想的矩形函数，这意味着fringe-washing函数不是sinc函数[15]。对fringe-washing函数应用Three-delay定标算法：以sinc函数近视fringe-washing函数的幅度，用二阶多项式来估计 fringe-washing函数的相位，其公式如式(8)所示。

2.5 可见度函数的归一化

在完成所有的预处理校正后，将所有的预处理过程结合到一起考虑，对得到的相关结果进行可见度函数归一化。文献[16]给出了可见度函数归一化的公式。

其中MMN是数字相关结果，rMN是 fringe-washing函数，TSYSMTSYSN是通道M,N系统温度。

为了验证以上算法，利用 MATLAB设计一个仿真平台，模拟综合孔径辐射计的一个二元干涉基线，研究了对可见度函数预处理的算法。这里我们主要讨论算法仿真的过程与结果。

3 二元干涉仪的仿真模型

采用蒙特卡洛方法，对一个基线的二元干涉仪进行仿真。在该时域仿真模型中，两路接收机注入同一噪声，并考虑接收机本身等效噪声。每个通道的接收机综合模型(物理器件上的各级放大器与各级滤波器的综合模型)化为低通滤波器。注入噪声和接收机噪声叠加后的噪声，经过滤波器滤波后，进行IQ混频。混频后得到了输入的I, Q复信号，对结果进行复相关运算得到相关输出。二元干涉仪的仿真模型流程框图如图2所示。

图2 二元干涉仪的仿真模型流程

注意：本仿真平台的所有的信号处理都是对基带信号的处理，这是由于基带信号携带了所需的信息且易于处理。以下示例考虑了一个最简单的二元干涉仪，以验证仿真系统的正确性。

示例：假定注入的噪声温度设置为 100 K，接收机等效噪声分别为400 K和625 K(所有噪声均假定是高斯噪声)，采样频率为500 MHz，模拟点数为106个点(对应积分时间为2 ms)，假定两路接收机的滤波器是完全相同的，由巴特沃斯求出数字低通滤波器截止频率为160 MHz。取100个点对理想相关输出结果进行观察，得到接收机输出结果如表1所示。其中，其灵敏度是根据理想灵敏度公式算出的。从以上的结果可见该仿真过程的正确性。

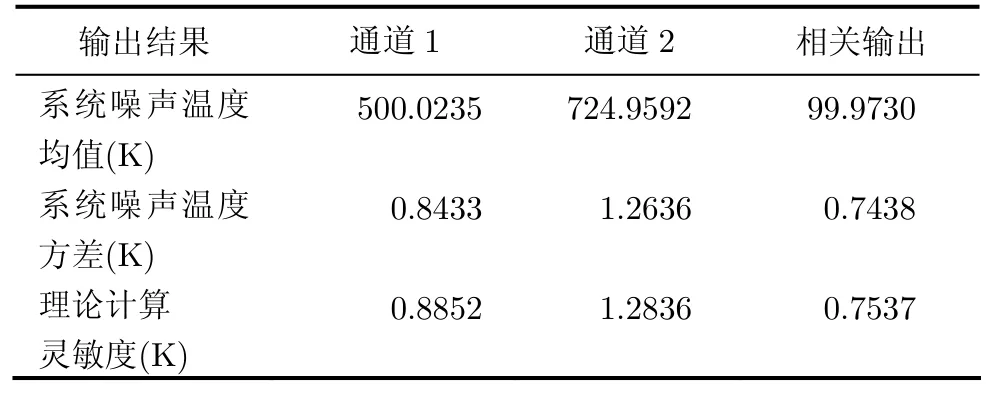
表1 示例的结果

4 可见度函数预处理的时域仿真研究

4.1 三阶量化及校正算法对相关结果影响的分析

复相关输出的结果与量化阈值有密切的关系，所以对信号进行三阶量化时，要考虑到量化电平的选择问题。尽量减小由量化门限引起的误差[11]。

实际应用中，希望在寻求数/模相关系数之间的关系时，了解估计算法所引进的误差。在最佳量化阈值下，利用估计算法得到模拟相关系数估计值与真值之间的关系如图 3所示。当模拟相关系数ρ≤0.5时，量化阈值设置为0.61±10%，从数字相关到模拟相关的估计结果的绝对误差的量级大约是10-5左右。由这两个估计算法引起的误差在我们可接受的范围内。

4.2 仿真模型中应用算法的结果

为了验证可见度函数的预处理算法，在以下的建模仿真中设置参数为：注入噪声温度为 100 K，接收机等效噪声分别为400 K和625 K，积分时间为2 ms，模拟点数为106个点。考虑了AD偏置的影响，三阶量化对复相关输出结果的影响，IQ非正交的影响，空间去相关的影响。首先，只测试每种校正算法的定标效果；然后，将所有偏置综合到一起，进行校正。

(1)AD 偏置校正的实验结果 设两个通道的AD偏置电平分别为量化后信号的累积平均，得到了初始相关结果后，对模型中AD偏置进行校正，可以得到理想的相关输出结果，结果如图4所示。可以看到，数据经过AD偏置校正后，有了明显的改变，便于进行后续处理。

(2)1.5 bit量化校正仿真结果 在上述AD仿真模型基础上，对接收机相关输出进行数/模相关系数的校正，图5画出了理想的模拟相关系数和通过校正得到的模拟相关系数之间幅度和相位的比较。校正得到结果与理想结果一致性良好，这也从侧面证明了上述AD偏置校正结果的正确性。

(3)IQ非正交校正结果 在示例的基础上，设置IQ非正交误差Δθ的值为0°～5°之间。对输出的相关结果进行校正，得到理想的复相关结果以及实际校正得到的复相关结果的 IQ两路的比及其误差如图6所示。从图中可见，校正后的误差小于0.1%。

图3 最佳量化阈值下实际和估计的模拟相关之间的关系

图4 AD偏置校正

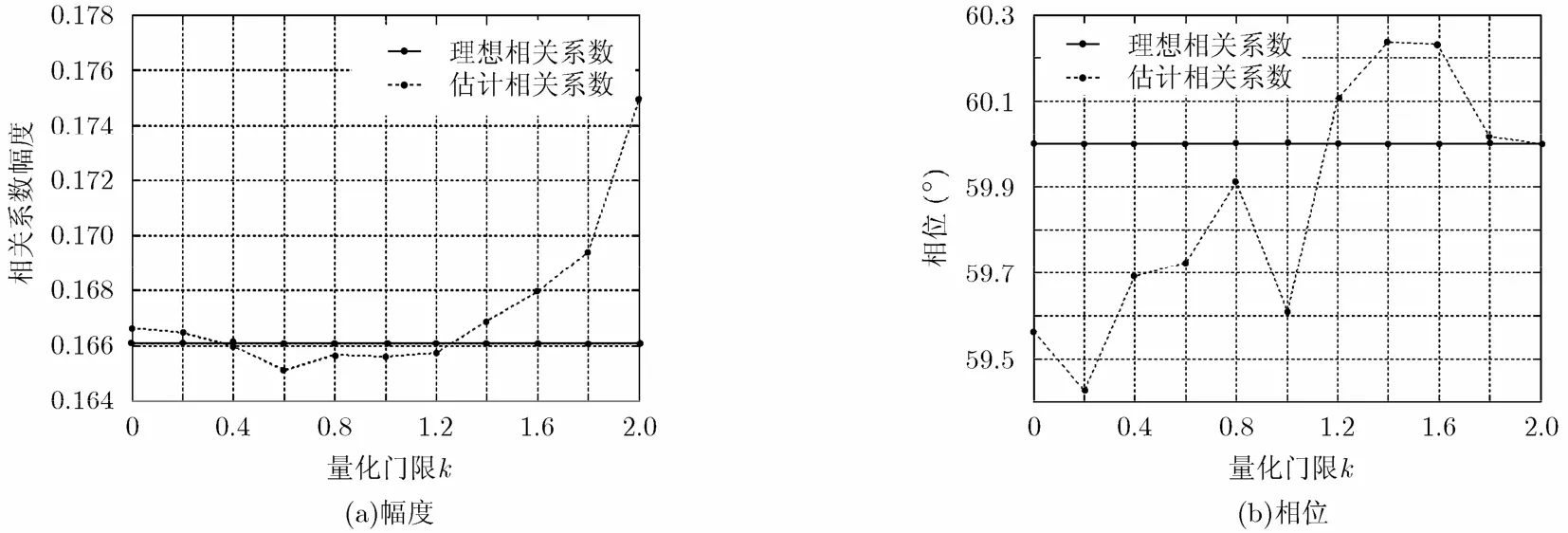
图5 校正后的模拟相关系数

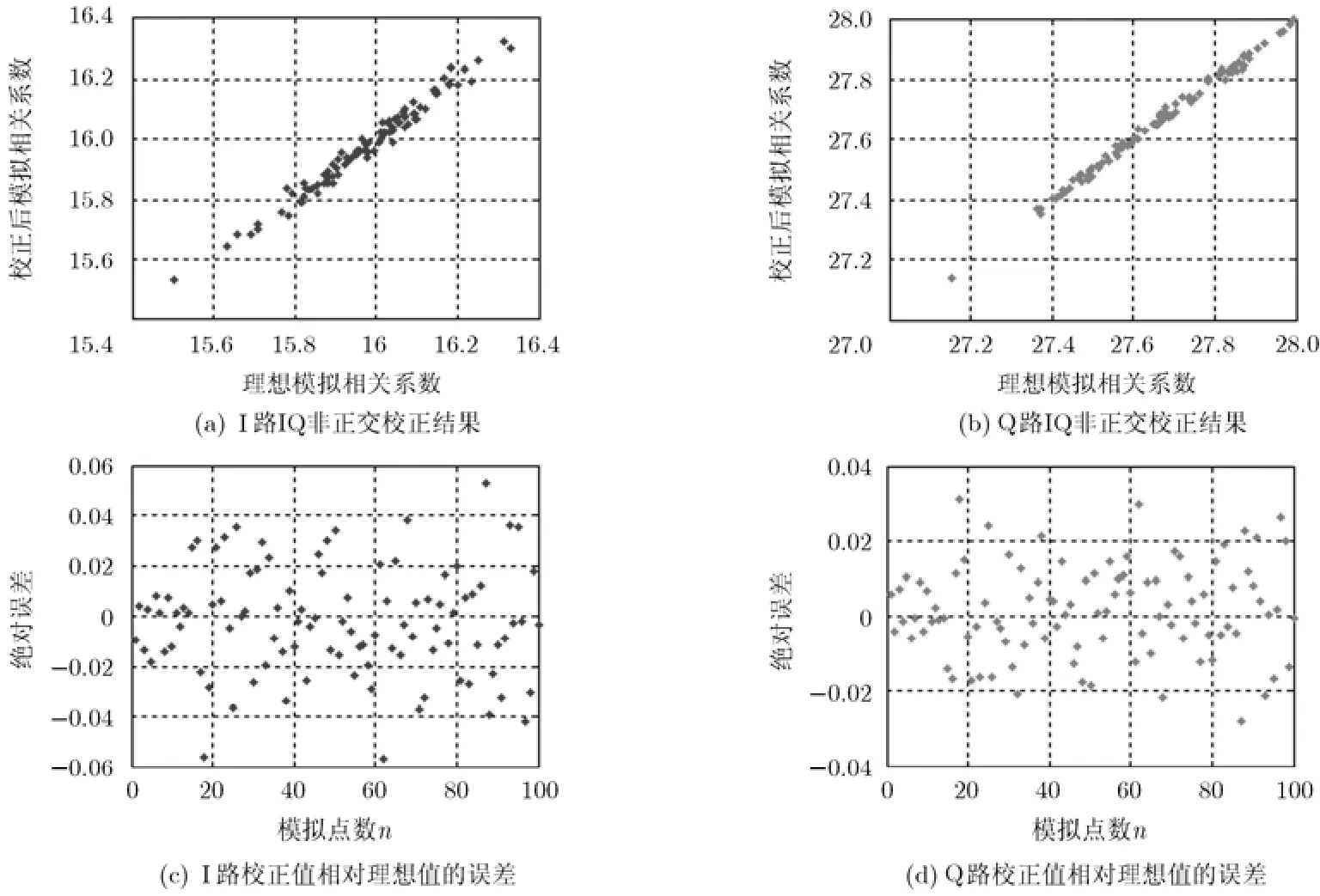
图6 IQ非正交校正结果

(4)Fringe-washing函数的校正结果 在示例基础上，将两套接收机的频率响应分别设置为五、六阶巴特沃斯低通滤波器，截止频率均为160 MHz。对两套接收机进行延时互相关，时延为-20～20 ns。利用three-delay方法测量fringe-washing函数，得到的校正结果如图7所示。从图中可见，利用threedelay方法，fringe-washing函数得到了较好的校正结果。两套接收机之间的延时相关输出仍然近似为sinc函数曲线形状。相关输出幅度和相位不理想的原因是两个接收机频率响应的幅度和相位的不理想性，以及幅度和相位信息不一致性。

图7 利用three-delay方法校正fringe-washing函数

(5)可见度函数预处理最终结果 将上述一系列定标进行综合，参数设置与之前一致(其中AD偏置电平为量化后信号的累积平均，量化阈值为最佳阈值，IQ非正交误差为 1°，接收机的频率响应分别为160 MHz截止频率的五、六阶巴特沃斯低通滤波器)，得到最终的校正结果如图8所示。同时为了对比该结果，得到了接收机的频率响应均为五阶巴特沃斯低通滤波器时的相关结果。从图中可见，当两个接收机频率响应一致时，理想的模拟相关系数值和校正后相关系数的峰值均为0.166；当两个接收机频率响应不一致时，理想的模拟相关系数值为0.166(其中，理想的模拟相关系数没有考虑 fringewashing函数的影响)，校正后相关系数的峰值为0.154，这是因为通道的频率响应不一致使相关结果产生了一个fringe-washing函数的相关因子。

5 地面样机实验对算法的验证

除了对可见度函数预处理算法进行了时域仿真的研究，本文利用“地球同步轨道毫米波大气温度探测仪”的地面样机系统搭载了两个实验，以验证可见度函数的预处理算法。其搭载的实验平台如图9所示。

在该实验平台中，利用接收机7输出的I路作为公共噪声注入到两路通道，接收机6、接收机8输出I路作为两个通道自身的信道噪声。调节3个通道的衰减，控制相关度改变。在数据处理上，由3个途径来得到模拟相关系数：功率计直接测量的结果估计模拟相关系数ρ；由8 bit自相关估计模拟相关系数ρ8bit；数据包输出的经过数字相关系数到模拟相关系数的校正得到的结果ρ'。其中以功率计直接测量噪声功率进而估计出的模拟相关系数可以作为一个较为可靠的参考。得到由这3种方法算出的模拟相关系数如图10所示。从图中可见，在改变其相关性后，5次不同设置得到的3种结果一致性良好。由此可见，该可见度函数的预处理算法的正确性。

图8 可见度函数预处理最终结果

图9 实验搭建模型框图

图10 3种方法算出的相关系数

6 结束语

干涉式综合孔径技术实现地球静止轨道的微波大气探测是该领域的发展前沿。本文所做工作是将三阶量化数字相关器的原始输出处理为可直接用于图像反演的可见度函数，即可见度函数的预处理。本文首先给出了可见度函数预处理的校正算法。然后利用MATLAB建立了一个仿真平台，对二元干涉仪进行时域的蒙特卡罗仿真，验证了可见度函数预处理校正算法的准确性。最后将该校正处理方法应用于“地球同步轨道毫米波大气温度探测仪”地面样机的成像实验，进一步验证了该算法的有效性。本文在时域对辐射计随机噪声的测量过程进行仿真，可以对三阶量化过程进行模拟。由此，可以通过其仿真结果为系统的优化设计及性能指标的定量化分析提供技术手段。

[1]Tanner A B,et al.. Initial results of the geostationary synthetic thinned array radiometer(GeoSTAR)demonstrator instrument[J].IEEE Transactions on Geoscience and Remote Sensing, 2007, 45(7): 1947-1957.

[2]The GAS team of ESA. Prototype mm-wave sensor to offer new view of Europe’s weather[OL]. http://www.esa.int/esaMI/Technology/SEMGS25NL9G_2.html. 2011, 9.

[3]Liu H, Wu J, Zhang S,et al.. The geostationary interferometric microwave sounder(GIMS): instrument overview and recent progress[C]. Proceedings of IEEE International on Geoscience and Remote Sensing Society’2011, Vancouver, Canada, 2011: F 24-29.

[4]Liu H, Wu J, Zhang S,et al.. Development of a three-element interferometer at 50～56 GHz for Geostationary Interferometric Microwave Sounder(GIMS)[C]. Proceeding of IEEE International on Geoscience and Remote Sensing Society’ 2010, Hawaii, USA, 2010: F 25-30.

[5]Liu H, Wu J, Zhang S,et al.. Conceptual design and breadboarding activities of Geostationary Interferometric Microwave Sounder(GIMS)[C]. Proceedings of IEEE International on Geoscience and Remote Sensing Society’2009, Cape Town, South Africa, 2009: F 12-17.

[6]Piles M, Camps A, Vall-llossera M,et al.. Downscaling SMOS-derived soil moisture using MODIS visible/infrared data[J].IEEE Transactions on Geoscience and Remote Sensing, 2011, 49(9): 3156-3166.

[7]刘浩. 干涉式全极化宽谱成像微波辐射计系统研究[D]. [博士论文], 中国科学院空间科学与应用研究中心, 2011.

Liu Hao. System study on the interferometric synthetic aperture radiometers with polarimetric and spectral observation capabilities[D]. [Ph.D. dissertation], Institute of Center for Space Science and Applied Research Chinese Academy of Sciences, 2011.

[8]Camps A, Corbella I, Vall-llossera M,et al.. The SMOS end-to-end performance simulator: description and scientific applications[C]. Proceedings of IEEE International on Geoscience and Remote Sensing Society’03,Toulouse, France,2003, 1: 13-15.

[9]Corbella I, Torres F, Duffo N,et al.. Interferometric radiometry measurement concept: the visibility equation[C].Proceedings of IEEE International on Geoscience and Remote Sensing Symposium’2011, Barcelona, Spain, 2011:3491-3494.

[10]Hagen J B, Farley D T,et al.. digital-correlation techniques in radio science[J].Radio Science, 1973, 8(9): 775-784.

[11]KulKarni S R, Heiles C,et al.. How to obtain the true correlation from a 3-level digital correlator[J].TheAstronomical Journal, 1980, 85(10): 1413-1420.

[12]Piepmeier J R, GasiewsKi A J,et al.. Digital correlation microwave polarimetry analysis and demonstration[J].IEEE Transactions on Geosciences and Remote Sensing, 2001,39(11): 2392-2410.

[13]赵锋, 苗俊刚, 万国龙, 等. 二维综合孔径微波辐射计接收机误差模型与校正方法研究[C]. 2009年全国微波毫米波会议,西安, 2009: 1630-1635.

Zhao Feng, Miao Jun-gang, Wan Guo-long,et al.. Error model and calibration method of 2D synthetic aperture microwave radiometer’s receivers[C]. 2009 National Conference on Microwave and Millimeter Wave, Xi,an, 2009:1630-1635.

[14]Torres F, Camps A, Bara J,et al.. On-board phase and modulus calibration of large aperture synthesis radiometers:study applied to MIRAS[J].IEEE Transactions on Geosciences and Remote Sensing, 1996, 34(4): 1000-1009.

[15]Butora R,et al.. Fringe-washing function calibration in aperture synthesis microwave radiometry[J].Radio Science,2003, 38(2): 1032-1046.

[16]Torres F,et al.. Denormalization of visibilities for in-orbit calibration of interferometric radiometers[J].IEEE Transactions on Geosciences and Remote Sensing, 2006,44(10): 2679-2686.