TPC自适应迭代译码方法

陈海飞，权进国，林孝康

(清华大学深圳研究生院现代通信实验室，深圳518055)

1 引言

1994年，Pyndiah等人［1］在 Chase算法的基础上提出了一种线性分组码的软输入软输出迭代译码算法，并将它应用于乘积码译码中，获得了很好的编码增益。由于其性能与Turbo卷积码较为相近。基于Chase算法的TPC迭代译码算法是一种通过缩小码字搜索范围的次最优译码算法。在译码时，将码元的对数似然比(Log-Likelihood Ratio，LLR)作为译码器的软输出，并将软输出信息减去软输入信息，作为下次迭代的外信息。通过这种方式不断修正码元的软信息，增大其可靠度，获得较好的译码性能。但是传统的迭代译码方法都是采用固定的迭代因子以及迭代次数，在信道的信噪比变化比较大的情况下，固定的迭代译码方法不能灵活的选择最优的迭代因子以及迭代次数，并且在低噪声信道环境下，较大的迭代次数会带来不必要的功耗浪费。针对以上问题提出一种自适应迭代译码算法，估算信道的信噪比，灵活地选择最适合的迭代因子，并根据译码的结果自动终止迭代译码。

2 TPC简介

2.1 TPC编码原理

以二维乘积码为例来讲述乘积码的构成。设分组码:C1(n1，k1，d1)和 C2(n2，k2，d2)。其中 n 表示编码长度，k表示信息比特长度，d表示最小汉明距离。二维乘积码P=C1⊗C2的构造方式如图1所示。

2.2 TPC SISO译码算法

Turbo乘积码是一种串行级联码，所以采用软判决迭代译码能提升Turbo乘积码的性能。最常用的就是Chase译码迭代算法。Chase算法是一种软输入硬输出的译码算法，其输出为硬判决信息，1998年 Pyndiah［2］针对 Turbo 乘积码提出一种基于修正的Chase译码算法的迭代译码算法。迭代译码结构由行、列译码器串行级联而成，结构如图2所示。

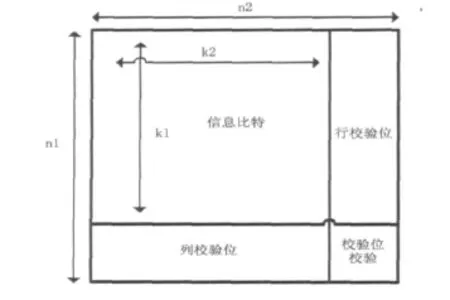
图1 二维TPC编码框图

图2 SISO迭代译码图

每一次迭代译码输入外信息W［m］，经过软译码单元计算输出外信息W［m+1］。如图2所示，在单元译码器中α［m］表示第m次迭代时的加权因子，β［m］表示第m次迭代时的可靠度因子。它们的值都是通过经验获得，在迭代初始阶段信噪比较大时，α［m］一般取值较小，主要用于抑制了外信息W［m］的作用，在迭代的后期，信噪比较小时，其值可以逐渐增大。β［m］主要用于控制软输出信息的输出峰值范围。

3 自适应迭代译码方法

大量实验表明，不同的迭代因子{α，β}在不同的信噪环境下对TPC迭代译码的收敛速度以及误码率影响很大。经典的Turbo乘积码译码算法采用固定的迭代次数和固定的迭代因子{α，β}，没有充分考虑到信道环境给译码器性能带来的影响，并且在低噪声信道环境下，较大的迭代次数会带来不必要的功耗浪费。

提出一种自适应Turbo迭代译码算法，针对不同的信道环境选择最优的迭代因子，并根据译码结果自动终止迭代译码。整个译码的原理框图如图3所示。

首先根据解调端输出的软信息R估算信道的信噪比，针对不同的信道环境选择合适的迭代因子，然后将软信息R及迭代因子送入Turbo码SISO迭代译码器，迭代终止判断单元检测每次译码的码字，并和上一次译码的码字做比较，当满足迭代终止条件时，结束译码并输出码字。

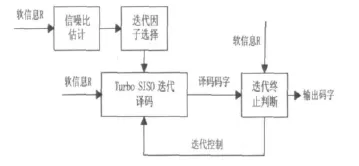
图3 自适应迭代译码框图

其中SISO迭代译码单元采用经典的Turbo乘积码迭代译码算法，在这里不详细介绍。论文的重心在于:信噪比估计单元、迭代因子单元、迭代终止判断单元。

3.1 信噪比估算单元

信噪比的计算公式复杂，不直接给出信噪比的计算公式，用一个与信噪比正相关的量S来表示信道的信噪比大小。设接收的软信息 Rn×m是一个n×m的矩阵，首先对R的每一个元素做硬判决得到矩阵K

然后根据行、列编码规则C1、C2对矩阵K做硬译码:硬译码可以先对K的行进行译码，再对K的列进行译码。得到译码码字Dhard。最后根据硬译码码字Dhard与软信息R估算信道环境。信道环境的好坏，表现为信道信噪比的大小，信噪比估算单元不直接计算信道信噪比，而用Dhard与R之间的距离来表示信道信噪比的大小:

3.2 迭代因子选择单元

迭代因子选择单元根据信噪比估计单元输出的信噪比S选择最合适的迭代因子α、β，作为SISO译码器的迭代因子。S与α、β的对应关系事先由MATLAB仿真获得。

3.2.1 S与α、β的对应关系

MATLAB仿真流程图如图4所示。

(1)生成一组信噪比测试向量SNR={snr1snr2...snrn}，预先设定一组备选迭代因子向量{α1，α2，α3，...，αn}，{β1，β2，β3，...，βn}

(2)选择信噪比snrk

(3)用MATLAB里生成信噪比为snrk的噪声序列n，生成发送码字c，则接收的软信息:r=c+n

根据公式2估算S

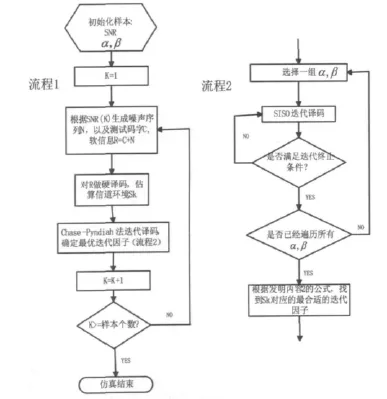
图4 MATLAB确定最优迭代因子流程图

(4)将软信息 R和每一个组合{αi，βj}送入SISO迭代译码器，找出信噪比Sk下最优的迭代因子。迭代因子好坏的评价标准为公式4。两个评价因子:误码率和迭代次数。

其中c是权重，f1(·)，f2(·)是归一化函数，将误码率和迭代次数映射到一个可比较的空间里。

(5)k=k+1，重复步骤(2)直至k=n。

(6)得到信噪比{S}与迭代因子{α、β}的对应关系。在这里设Sk对应的迭代因子为{αk、βk}

3.2.2 选择合适的迭代因子

仿真得到的信噪比{S}与迭代因子{α、β}的对应关系点数有限，是离散的集合。实际应用中信噪比估算单元输出的可能不属于仿真集合{S}，为了得到合适的迭代因子{、}，可以对离散的{S}与{α、β}的对应向量进行线性插值，插值的公式如下:

设Sk≤＜Sk+1，则线性插值得到的迭代译码因子{α=、β=}为:

3.3 迭代终止单元

最大似然译码是在许可码字空间找到与输入软信息R距离最小的码字作为译码输出。随着迭代次数的增加，信噪比逐渐减小，但是迭代次数达到一定程度之后，进一步的迭代译码并不能更进一步降低误码率。迭代终止单元给出一种低复杂度的迭代终止判断方法，自适应的选择迭代次数。根据迭代译码输出的码字Dn与上一次译码输出Dn-1的距离来判断译码器是否继续迭代。距离的计算方法如下:

判断依据为:若dis(n)≤H终止迭代，否则继续迭代。其中H是迭代门限，迭代门限的值与TPC编码方案有关，一般根据实际的应用取经验值。

4 仿真

以二维TPC为例，采用经典的Chase-Pyndiah作为迭代译码单元，仿真自适应迭代译码器的性能。TPC信息矩阵每行的编码 C1为 hamming(63，57，3)，每列的编码 C2为 hamming(63，57，3)。

由仿真图5所示，随着性噪比增加，译码器迭代次数减少。仿真图6是固定迭代译码算法与自适应迭代译码算法的误码率比较，结合图5与图6可见，在低信噪比信道里，自适应迭代译码的迭代次数比较高，误码率比固定迭代译码算法低，这保证了在低信噪比信道里自适应迭代译码器的性能。在信噪比较高的情况下，自适应迭代译码器的迭代次数很小，这样有效降低了译码功耗。

图5 迭代次数与信噪比仿真图

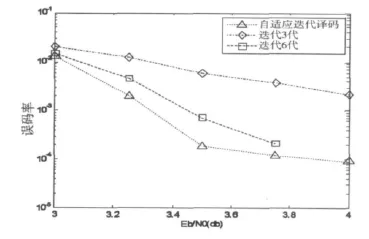
图6 不同的迭代译码器误码率比较

5 结束语

对传统的TPC迭代译码算法提出改进，提出了一种自适应迭代译码算法。与传统的TPC迭代译码算法相比自适应迭代译码算法更加灵活，适用于信道环境多变的应用场景。

详细介绍了自适应迭代译码器的核心单元:信噪比估计单元、迭代因子单元、迭代终止判断单元，最后以 C1=C2=Hamming(63，57，3)的二维 TPC 编码方案进行了仿真。实验结果表明自适应迭代译码在低信噪比信道环境下误码率较低;在高信噪比信道环境下迭代次数较小，有效的降低了功耗。

［1］ PYNDIAH R，GLAVIEUX A，PICARTA，et al.Near optimum de-coding of product codes［C］.//1994 IEEE GLOBECOM.NewYork:IEEE，1994:339-343.

［2］ Pyndiah R.Near-Optimum Decoding of Product Codes:Block Turbo Codes［J］.IEEE Trans.on Communications，1998，48(8):1003-1010.

［3］ Pyndiah R，Combelles P，Adde P.A very low complexity block turbo decoder for product codes［C］.//Communications:The Key to Global Prosperity，1996:101-105.

［4］ Chase D.A Class of Algorithms for Decoding Block Codes with Channel Measurement Information［J］.IEEE Trans.Inform.Theory，1972，18(1):170-182.

［5］ Hirst Simon A，Honary Bahram，Markarian Garik.Fast Chase Algorithm with an Application in Turbo Decoding［J］.IEEE Trans.on Communications，2001，49(10):1693-1699.