区间人口数据插值/调整方法及其应用
2012-07-25王桂新
王桂新
1 区间人口数据缺损插值方法及步骤
1.1 区间人口数据缺损插值的基本方法
对两时点之间缺损(或异常)人口数据的插值(或调整),实质上也是一种人口预测,所以人口预测方法同样适用于两时点之间时间系列缺损人口数据的插值。关于两时点之间时间系列缺损人口数据的插值,包括人口数量、年龄结构数据插值等多方面的内容。适用于区间时间系列人口数据插值的人口预测方法,主要有数学方法和人口增长因素分解法。限于篇幅,本文只介绍区间人口数量插值的数学方法。
所谓区间人口数量插值的数学方法,即根据数学方法和人口静态统计数据,在分析和模拟已有人口数据变化趋势的基础上建立人口增长模型,并用以推算区间某一缺损值的方法。用于区间人口数量插值的数学方法,主要有以下几种:
(1)假定以算数级数增长的直线插值方法
根据对已有人口数据(或样本数据)变化趋势的考察分析,如果判断人口数量变化基本按算术级数增长,那么就可以用按算数级数增长的直线模型推算的方法进行插值,其插值推算模型为

其中,Pt为需要插值的t时点的人口,P0为期初人口,PN为期末人口。这种方法适用于时间较短、人口数量增长规模相对比较均匀的区间人口插值,在正常情况下以年度数据推算年内各月人口数据时多采用在这种方法。
(2)假定以几何级数增长的曲线插值方法
如果根据对已有人口数据(或样本数据)变化趋势的考察分析,发现人口数量变化基本按几何级数增长,那么就需要用以几何级数增长的曲线模型推算的方法进行插值。这种插值方法,对已有人口数据多用指数曲线(即复利曲线)进行拟合,较适用于封闭地区时间较短、人口增速比较均匀的区间人口插值,其基本模型为
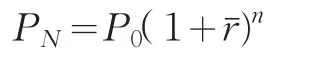
其中,P0为期初人口,PN为期末人口为人口年均增长率,n为考察期间的年数。这种方法,关键是通过变换

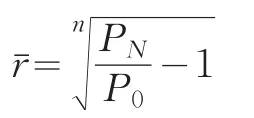

然后再根据公式推算出需要插值的t时点的人口数Pt。
(3)根据一般趋势曲线模型的插值方法
如果根据对已有人口数据(或样本数据)变化趋势的考察分析,发现人口数量变化曲线并非符合几何级数,这时可根据已知人口数据拟合建立一般趋势曲线模型进行插值。采用一般趋势曲线模型进行插值,通常使用2次曲线、3次曲线、指数曲线等趋势线模型,但有时也用其他趋势线模型。究竟使用哪种趋势线模型更合适,可通过多次模拟结果做出判断和选择。这种方法比较适用于时间较短、人口呈加速增长态势的区间人口插值。
例如,可对已有人口数据用2次多项式进行回归分析,由此建立的基本曲线模型为

其中,Pt为需要插值的t年的人口数,a、b、c均为参数。
如果人口的加速增长曲线比2次多项式曲线还陡峭,可选用3次多项式曲线进行拟合,并建立相应的趋势曲线插值模型

同样,式中Pt为需要插值的t年的人口数,a、b、c、d均为参数。
当然,如果发现人口呈指数增长趋势时,就要用指数曲线式进行回归建模。
(4)根据极限增长曲线的插值方法
对一定区域来说,在一定约束条件下,人口数量增长往往会存在一定的极限规模,这时就需要用存在一定极限的增长曲线模型进行插值。存在一定极限的增长曲线主要有变形指数曲线、冈巴兹曲线(Gompertz curve)和逻辑斯特曲线(Logistic curve)。关于拟合建立变形指数曲线模型、冈巴兹曲线(Gompertz curve)模型和逻辑斯特曲线(Logistic curve)模型的具体方法可参阅笔者拙著《区域人口预测方法及其应用》(华东师范大学出版社,2000年出版),在此不再赘述。
1.2 区间人口数据缺损插值的一般原则和步骤
1.2.1 区间人口数据缺损插值的基本原则
由前述可以看出,对区间缺损人口数据进行插值,关键是建立一个插值模型;而要建立插值模型,关键又是需要获得数量足够、质量可靠的样本数据(已有数据),而且建立的模型及其参数都要通过统计检验,最后计算的插值模型值与实际值的相对误差率都不能太大。具体地说,进行区间人口数据缺损插值,一般应遵循以下原则:
首先,用于建立插值模型的样本数据,数量要充足,质量要可靠。根据回归分析建模,样本数据一般应在10个以上。而进行区间缺损人口数据插值,多属在两次人口普查、即10年之间插值,所以要求的样本数据可以少一些,但最好也不能少于六、七个,至少不能少于要插值的个数。
其次,建立的插值模型及其参数都要通过统计检验。对模型来说,说明系数R2最好达到95%以上。如果模型精度达到95%以上,其参数一般也都会通过检验。
第三,建立插值模型以后推算的年度人口模型值与实际人口值(已有样本数据值)的相对误差率一般应控制在95%以上,最好能达到1%以内。这样才能保证模型插值更逼近于实际人口值。
1.2.2 区间人口数据缺损插值的一般步骤
第一,要收集数据,并评估数据质量。如对尚未进行常规年度统计的常住人口进行区间插值,要收集足够数量的常住人口样本数据,并对收集的常住人口样本数据进行质量评估。评估常住人口样本数据的质量,最简单、有效的方法,就是通过绘制样本数据的点子图,看其样本数据的分布有没有突变的异常数据,如果样本数据的分布都很有规律,即说明样本数据的质量是比较可靠的。
第二,建立区间缺损数据插值模型。根据上面绘制的样本数据点子图形状,确定选用怎样的曲线模型模拟更合适。如果点子图显示人口数量基本呈均匀增长态势,可选用模型(1)模拟建模;如显示人口数量基本呈加速增长态势,可选用其他几种趋势曲线模型进行模拟建模。模拟建模可以直接用EXCEL或SPSS等软件实现。在模拟建模时,可以建立几个插值模型供比较选用。
第三,检验模型。检验模型包括三个方面。一是进行统计检验。如果对样本数据用EXCEL或SPSS等软件进行模拟建模,可以直接给出对模型的统计检验结果。二是计算和比较所建插值模型理论值与实际人口值的相对误差率,选用各年相对误差率都普遍较小的插值模型。实际上,以上这两种检验在效果上是一致的。三是间接检验,如已有研究证明年度人口数量与GDP规模密切相关,所以也可以根据已知的GDP规模变化趋势检验根据插值模型计算的年度人口数量的变化是否合理。
第四,对模型和插值进行解释。也就是对为什么采用某个插值模型及其插值做出客观解释。如对上海“五普”与“六普”之间常住人口数量变化建立的插值(或调整)模型,可结合宏观经济形势及上海城市发展与人口发展政策等给出客观、合理的科学解释。
2 区间人口数据缺损插值方法应用——以上海为例
上海统计部门根据人口普查及相关调查数据,每年都发表全市常住人口数,表1即为统计部门发表的2000~2009年间每年的常住人口数。2011年4月市计划生育部门率先发表了上海2010年常住人口数为2221(2220.83)万人,此后统计部门又发表了2010年上海人口普查的常住人口数为2302(2301.91)万人,比计生委部门发表的年末常住人口数还多81万人。不管是计生委部门发表的年末常住人口数,还是统计部门发表的10月末人口普查常住人口数,与以前发表的1999年的常住人口数比较,分别增长了300万和381万人。表1显示,上海年末常住人口连续多年年增数基本都在三、四十万人左右,而2010年甚至不到1年就增长了380多万人,这显然是超越常规、令人质疑的。为了获得上海相对较能反映实际的常住人口数,必须对其2000~2010年间的年末常住人口数进行适当地调整和整合。看起来这属于数据调整,但其实质与缺损数据插值原理及方法是一致的。
由于常住人口数据主要来源于每10年进行一次的人口普查及中间每5年进行一次的人口抽样调查。尽管对常住人口(主要是外来常住人口)调查比较困难,统计误差较大,但相对其他来源的常住人口数据,每10年进行一次的人口普查所获的常住人口数据仍然被认为信赖度最高,并仍被作为评价其他数据可信性的参照依据。因此,本文对2000~2010年间的年度常住人口数进行调整,也将以2000年和2010年人口普查获得的常住人口数为基准。
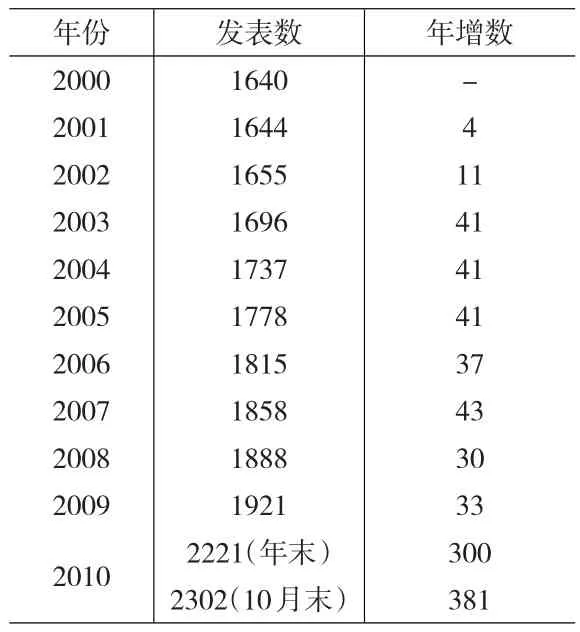
表1 上海市发表常住人口数 (万人)
2.1 数据收集、评价及调整模型建模
2.1.1 数据收集和评价
根据前述步骤,首先要收集和评价现有数据。收集的上海常住人口数据已如表1所示。对此,有几个问题需要讨论和评估。
一是上海2010年一年常住人口是否能暴增三百多万人甚至更多。根据作者多方面的调查,对此概括起来主要有两种看法:一种看法是2010年上海常住人口的增长受到世博会很大影响。他们认为由于世博会的举办,吸引了更多的外来人口到上海务工经商,从而使上海外来常住人口显著增长。尽管在人口普查时已注意尽量减少世博会的影响,但这种影响很难消除。这种看法实际上就是认为上海2010年常住人口由于受世博会的影响而暴增,但人口普查的常住人口数未能剔除因世博会影响而引起的常住人口的非正常增长;另一种看法是上海2010年的常住人口数量基本没有受世博会的明显影响,世博会对上海常住人口增长的影响在世博会举办之前的建设期即已表现出来。这种看法实际上就是认为上海2010年常住人口因世博会影响一年暴增三百多万人是不可能的,人口普查的常住人口数基本反映了上海常住人口规模,但它是2010年及之前多年增长的结果。根据对人口普查获得的上海全市不同年份“离开户口登记地时间(R8)”的外来常住人口的参考性分析,结果并不支持第一种看法,但能佐证第二种观点。对杨浦区人口普查数据的分析结果也同样如此。
二是在包括2010年的“十一五”期间上海常住人口呈怎样的增长态势。根据上海市有关部门调查,上海近年外来常住人口呈加速增长趋势,如嘉定区“十一五”期间来沪人员总量从2006年的58万增长到2010年底的79万(居住六个月及以上者为73.1万),平均每年增加8~10%。普陀区外来常住人口也呈同样的加速增长趋势,如其2006年、2008年和2010年来沪常住就业人口分别为46.83万人、74.50万人和101万人。有关部门对上海郊区四区的调查还发现,在“十一五”期间外来常住人口呈倍增趋势。这说明,表1中“十一五”期间2010年之前几年的常住人口规模及其增长,并未真正反映上海常住人口的实际增长变化。
三是2005年全国1%人口抽样调查时上海的抽样比为3.18%,一般来说至少在人口总量层次上按此推算的常住人口规模应该具有相当的代表性。但推算结果显示,以当时的调查样本人口和抽样比推算的常住人口数为1646万人,几乎与2000年人口普查数据相等,这显然是偏小的。表1中发表的2005年常住人口数为1778万人,说明统计部门已经根据当时的实际情况对包括2005年的“十五”期间每年的上海常住人口数据进行了调整。该发表数据已得到广泛应用,而且也没有相关调查说明其不符上海当时常住人口的增长情况,所以可以认为上海“十五”期间年度常住人口数据是比较符合实际的,可以用作本次常住人口数据调整的样本数据。
基于以上可得结论:第一,2010年上海常住人口数量并未因世博会影响而出现骤然暴增现象,而是2010年及之前多年增长的结果;第二,表1中“十一五”期间2010年之前几年的常住人口规模及其增长未能反映上海常住人口的实际增长变化,需要进行调整处理;第三,“十五”期间常住人口数据则相对比较符合实际,可作为调整“十一五”期间2010年之前几年常住人口数据的基础样本数据。所以,对上海“五普”、“六普”两次人口普查(2000~2010年)之间年度常住人口数据调整插值,可把上海“十五”期间5年和2000年、2010年等年份的常住人口数据作为基础样本数据,以此建立拟合调整模型,计算“十一五”期间2010年之前几个年份常住人口的调整值。
2.1.2 调整模型选择与建模
基于以上调查和分析,通过对上海常住人口多种数据的尝试,以及采用多种方法的探索性拟合,发现上海常住人口数量的增长,可用前述的多项式曲线模型进行拟合。事实也说明用该曲线模型拟合效果较好,尤以3次多项式模型拟合效果最好。
为了建立拟合调整模型,并为避免引发更大的人口规模“恐大症”和简单起见,本文首先把2000年人口普查的1640万人和2010年人口普查的2302万人分别作为当年年末的常住人口数①现有统计年鉴已把1640万人作为2000年的年末常住人口数。。这样就可直接根据表1中的历年常住人口数据,采用逐步去掉“十一五”期间2010年之前几年常住人口“异常”数据的方法进行反复拟合,直到建立满足目标精度的拟合模型。当然,在达到目标精度的前提下,去掉的年度数据应该尽量少,这样可以保留更多的数据以满足回归分析的样本要求。拟合分析结果显示,去掉3到4年的“异常”数据即可建立高精度的2次曲线和3次曲线拟合调整插值模型。根据拟合分析结果,本文对上海2000~2010年间年度常住人口的调整提供了以下2个方案。
2.2 上海2000~2010年间年度常住人口调整结果
2.2.1 调整方案Ⅰ
该方案假定表1中2009年、2008年、2007年3年的常住人口数为需要调整的“异常”数据。因此,根据2000~2006年和2010年共8年的常住人口数据进行拟合分析,建立相应的2次曲线模型1和3次曲线模型2,据其计算的2009年、2008年、2007年的常住人口调整值分别如表2和表3所示。
模型1
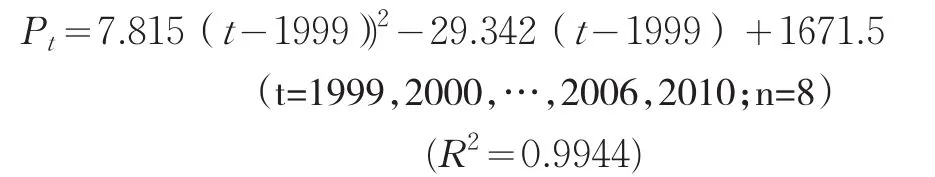
模型2
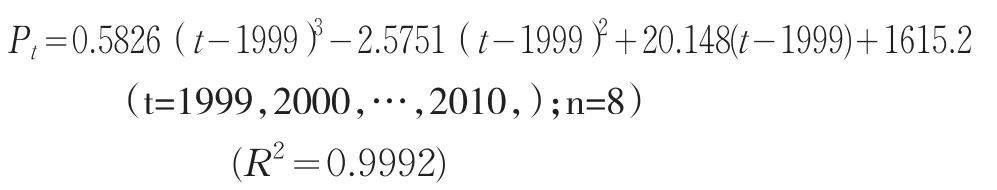
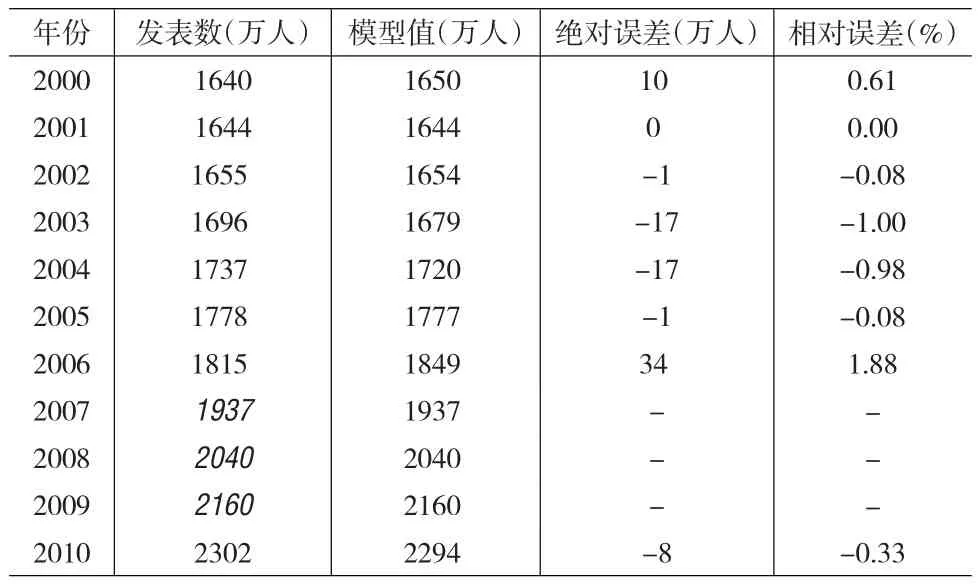
表2 根据模型1的拟合计算结果
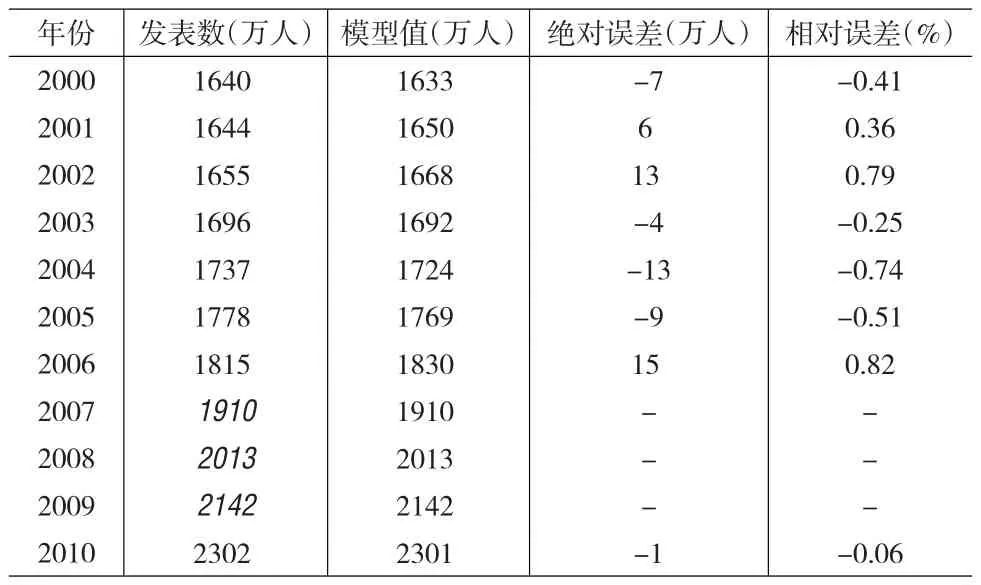
表3 根据模型2的拟合计算结果
2.2.2 调整方案Ⅱ
该方案假定表1中2009年、2008年、2007及2006年4年的常住人口数为需要调整的“异常”数据。因此,根据2000~2005年和2010年共7年的常住人口数据进行拟合分析,建立相应的2次曲线模型3和3次曲线模型4,据其计算的2009年、2008年、2007年及2006年的常住人口调整值分别如表4和表5所示。
模型3
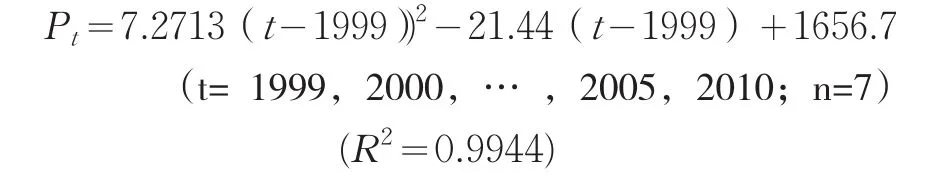
模型4


表4 根据模型3的拟合计算结果
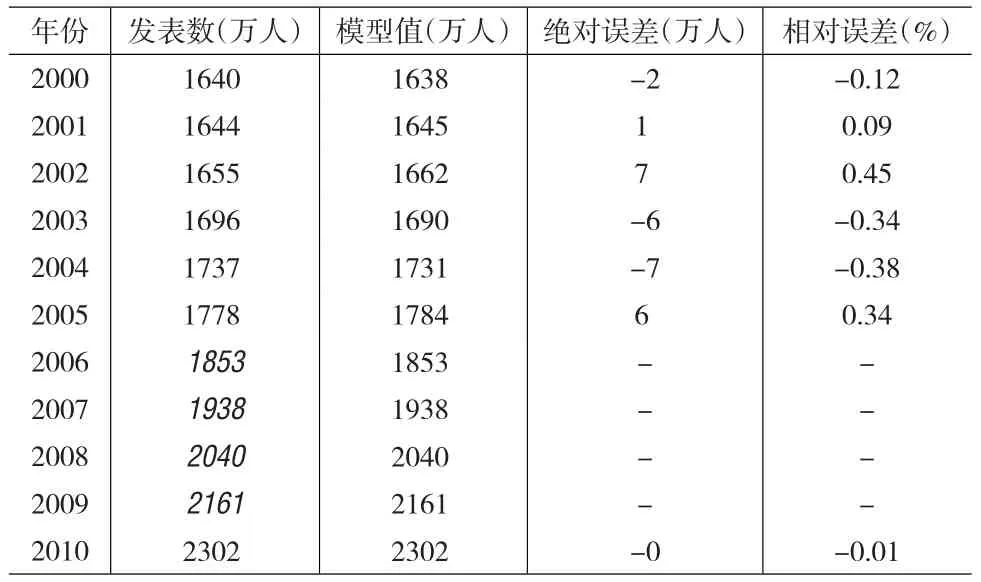
表5 根据模型4的拟合计算结果
2.3 两种调整方案的比较与讨论
根据以上拟合分析结果可知,两种方案的4个拟合调整插值模型,说明系数R2都在99%以上,具有很高的精度。但从4个模型计算模型值与实际值的误差看,模型1计算模型值与实际值的相对误差率最大年份达1.88%,其他3个模型的计算结果,年度常住人口数的绝对误差都基本小于15万人,相对误差率都基本在0.8%以下,其中尤以模型4的拟合效果最佳,模型值与实际值的绝对误差都在7万人以下,相对误差率都小于0.45%。所以,对上海2000~2010年间各年末常住人口数的调整插值,可优先考虑采用模型4的计算调整结果。
根据模型1~模型4计算调整后的上海2000~2010年每年的常住人口数和户籍人口数(表6),可计算出每年的外来常住人口数(表7)。由此可以看出,根据模型2、模型3、模型4计算调整的上海“十一五”期间常住人口数量均呈加速增长趋势(图略),而且也都基本呈倍增态势。该结果与前述的调查分析结论相同。这也从一个方面说明了本文调整插值方法的科学性和调整插值结果的合理性。

表6 根据模型1-模型4调整计算后的上海常住人口数
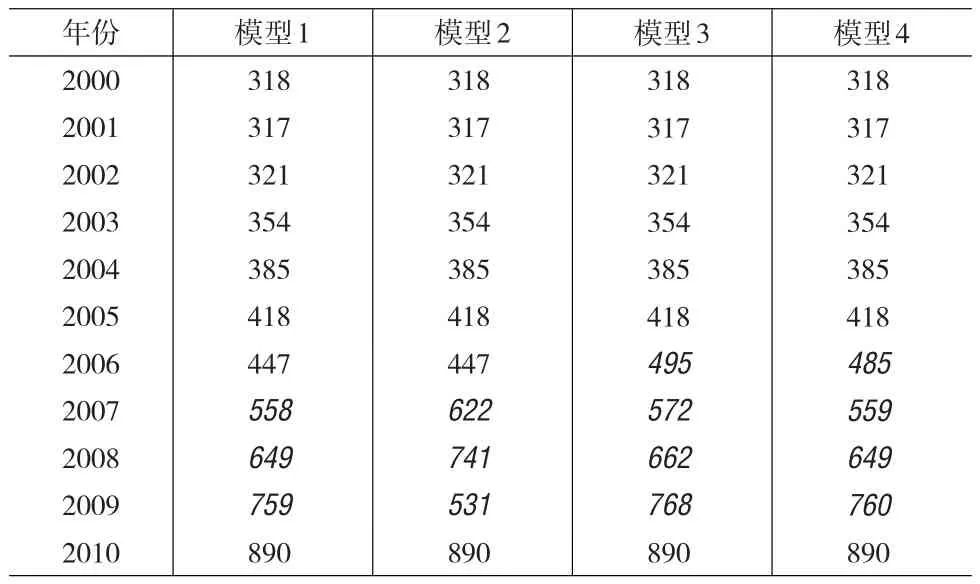
表7 根据模型1-模型4拟合计算的上海外来常住人口数
[1] 王桂新.区域人口预测方法及应用[M].上海:华东师范大学出版社,2000.
