汽车座椅安全带固定点强度试验仿真模型改进

曹 奇 成艾国 周 泽 吴 飞

湖南大学汽车车身先进设计制造国家重点实验室，长沙，410082

0 引言

《汽车座椅安全带安装固定点》是汽车被动安全中要求必须通过的重要法规。本法规试验是一种破坏性试验，即一台白车身仅能进行一次试验。重复的实车试验必然造成大量的物资和时间浪费，因此在实际中多采用CAE仿真的方法来模拟这一试验过程。目前国内类似的准静态仿真主要基于隐式［1］和显式［2－6］两种有限元方法，但是隐式方法存在较大收敛性问题，需要花费大量时间进行前处理，而显式分析模型计算精度通常低于隐式分析模型的计算精度。许多设计机构采用的仿真模型精度和稳定性有限，不能很准确、可靠地预测试验结果，导致在节省成本和缩短时间上效果有限，从而缺乏说服力。本文通过考察常用的两种仿真方法的优劣，选用较为合理的显式有限元方法，并根据多次仿真和试验对比，对传统仿真模型中的关键参数进行逐步修正，最终得到与试验高度吻合的结果。经多次重复试验验证表明，本文得出的结论能够可靠地提高仿真精度，切实减少人力、物力和时间浪费。

1 显式分析与隐式分析理论

对于一般的物理模型，总是可以建立下面的运动方程：

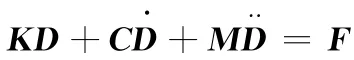
式中，K为刚度矩阵；C为阻尼矩阵；M为质量矩阵；D为节点位移；F为载荷。

任何一个物理过程，在仿真软件中总是被抽象为上述运动方程。在求解这一物理模型的过程中，显式分析和隐式分析都率先计算模型节点加速度，然后通过节点加速度积分依次求得节点速度和位移，两者区别在于求解加速度的方法上。

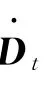
隐式分析采用迭代法，以常见的NewMark法为例。首先假设

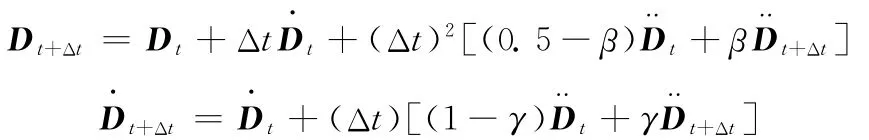
其中，β、γ是分析者根据系统特征人为设定的系数。上述假设在γ≥0.5且β≥（2γ＋1）2/16时是无条件稳定的。经过推导，得到

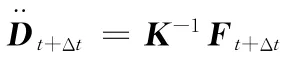
其中K矩阵求逆的过程很复杂，这就使得隐式分析耗费大量的计算资源。

隐式算法可以设置较大的时间步长，但是在面对复杂接触和非线性问题时，大的时间步长会使解的收敛异常困难，因此不得不减小时间步长以获得稳定合理的结果，甚至减小到与显式算法时间步长等同的程度，此时将耗费巨大的计算资源，而显式积分法能够简单有效地描述这些问题。因此，在模拟高速动力学事件、复杂接触问题、非线性准静态问题时，选用显式积分方式更有优势，这也是国内外主流技术机构越来越多采用显式方法的原因。

2 安全带拉伸试验简介

安全带拉伸试验用来验证车载安全带系统在车辆紧急减速时是否具备足够的强度为乘员提供保护。通过图1所示的上下人体模块，沿车辆纵向中心平面与水平方向成向上（10±5）°的方向施加力载荷，以尽可能快的速度加载至规定值，并至少持续0.2s。通常整个实车试验过程持续15s左右。对于三点式安全带，上下人体模块规定值均为（13500±200）N，对于两点式安全带，上车体模块为（13500±200）N，下车体模块为（22250±200）N。此外，如果有安全带安装点位于座椅上，还应加入相当于20倍座椅重力的力。

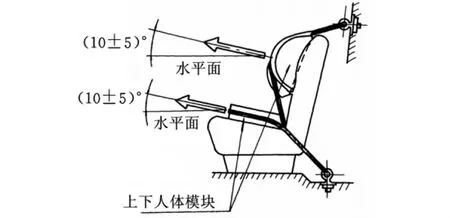
图1 安全带试验加载示意图

3 分析模型

利用有限元前处理软件Hypermesh建立如图2所示的安全带试验仿真模型。取D柱安全带安装点螺栓附件位置上一点，通过比较仿真与实际试验中该点的位移，来判断仿真模拟的精确程度。在仿真模型中，该节点号为2107497。

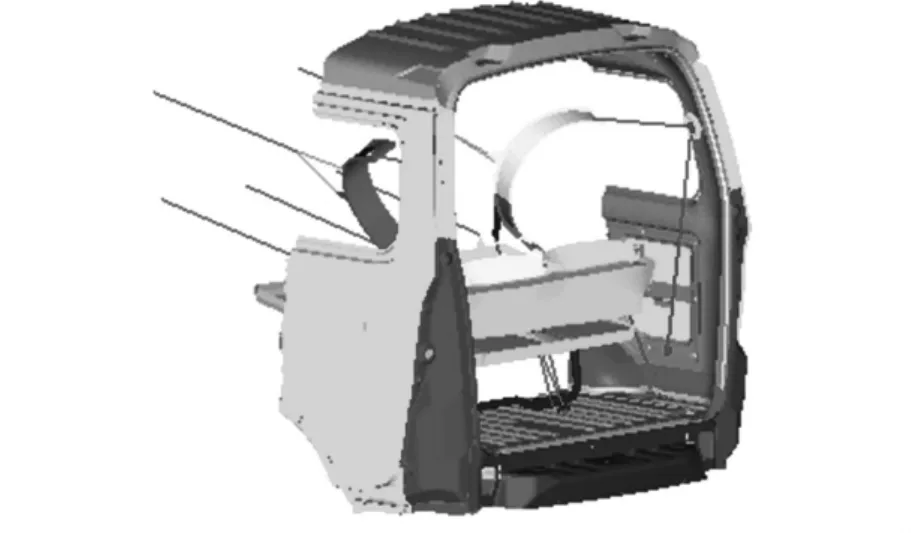
图2 安全带试验仿真分析模型

图3所示为初步建立的模型仿真结果与实车试验结果，对比可见，两者有较大差距。

图3 实车试验与初步仿真结果对比

实际试验中，所选参考点位移为96.5mm，而在初步仿真模型中，这一参考节点位移达到127.256mm，后者比前者大31.6%。这一仿真结果低估了结构的强度，因而，在此仿真技术基础上设计出的结构强度太过保守，从而提高了整车成本。下文将对单元类型、加载速度、加载方式、网格优化四个方面逐步进行分析调整，提高仿真精度。

3.1 单元类型选取

3.1.1 HL单元

HL单元基于薄壳单元的两点基本假设：①垂直于中面的线应变可以忽略；②与中面平行的截面上法向应力可以忽略。

HL单元是从8节点体单元通过压缩降级得到的，因此与体单元兼容性非常好。这样，可以沿用LS－DYNA之前为体单元开发的各种技术。由于上述两点假设只有在大位移和大应变条件下才认为是成立的，因此，HL单元适用于大位移和大应变问题的研究，但其缺点表现为需要耗费大量的计算时间。

3.1.2 BT单元

由Belytschko和Tsay共同开发的BT单元于1981年在LS－DYNA中得到应用，其主要优势在于保证计算精度前提下有超高的计算效率。与HL单元相比，在采用厚度方向5点积分的情况下，BT单元仅需做725次数学操作，而HL单元需要做4050次数学操作，选择性缩减积分HL单元更是需要做35 350次数学操作。

BT单元算法之所以高效，是因为采用了如下两点简化处理手段：①通过嵌入一个基于节点的固定坐标系分离了旋转分量，避免了复杂的非线性力学特性；②在组集方程时，采用柯西应力矢量的形式，简化了计算应力分量的难度。

在单元节点共面的情形下，这两点简化不会对计算精度造成任何影响，且能大幅减少计算耗时。传统仿真模型中通常采用BT单元的形式进行计算。

3.1.3 BWC单元

由于BT单元局部坐标系是建立在平面几何上的，故对于单元节点不共面的情况，即所谓的扭曲梁问题，BT单元无法给出合理的答案。BWC单元通过新增一个单元翘曲变形刚度，加入了单元扭曲的计算，从而对这一缺陷进行了修正。

3.1.4 全积分单元

BT单元和BWC单元都采用了缩减积分的方式，在单元面内只使用一个积分点，减少了积分次数，从而进一步提高了计算效率，同时引入了沙漏模式来控制缩减积分带来的零能模式。全积分单元采用与BT单元相同的单元坐标系，但是在线性四边形单元平面内选择2×2个积分点，能够处理单元的弯曲问题。如今在计算机硬件条件已经大幅改进的情况下，使用全积分单元的计算时间已经变得可以接受，而且其计算结果更加真实、精确。

3.1.5 结果对比

表1列出了选取四种单元得到的节点位移和计算时间。可以看出，BT单元和BWC单元分析结果区别不大，而全积分单元虽然计算时间稍长，但与BT单元相比，节点位移减小了8%。HL单元计算时间和计算精度都处于居中的水平。因此采用全积分单元使仿真结果更准确。在后续分析中，将采用全积分单元取代BT缩减积分单元。

表1 选取四种单元得到的节点位移和计算时间

3.2 加载速度选取

对于准静态模拟而言，加载时间的确定是一个关键问题。对于一般的物理过程，如果按照其固有持续时间来加载，可以确定将获得一个准确的解。而在实际仿真中，为了缩短计算时间，需要人为地提高载荷速率，只要能够控制模型的动态效应，使结果受到惯性效应的影响很小，就可以认为等同于准静态情况。由文献［3］可知，加载速率在40km/h以下时显示计算结果与准静态结果非常接近。而本试验并不以速度为输入条件，因此加载速度难以控制。事实上，结构的最低模态，决定了其动态效应被激发的临界点［7］。本文首先计算仿真模型的局部模态，然后以其最低模态为参考，确定合适的加载速度。

对安全带固定点局部模型进行模态计算，得到一阶模态仿真结果如图4所示。

图4 安全带试验仿真模型模态分析结果

根据仿真结果，该安全带固定点局部结构的最低模态为76.1Hz，对应周期为12.5ms。当载荷周期为12.5ms时，顶盖位置将发生共振，产生严重的动态效应。为了避免这种情况发生，应使载荷周期大于12.5ms。为此，加载时间分别取50ms、75ms、100ms、125ms，并分别保持20ms。

表2列出了在不同加载时间的情况下计算得到的节点位移及计算时间，其中，ts为实车试验的加载时间，模型单元采用全积分单元。

表2 不同加载时间下的节点位移和计算时间

结果表明，加载时间从50ms增加至75ms时，模型计算结果有较大改进，节点位移的改进量约为17%，在加载时间为75ms时，节点位移的计算结果最接近实车试验结果。继续延长加载时间，仿真节点位移比实车试验值逐渐偏小。因此，加载时间为75ms，即等同于模型最低模态对应周期的6倍时，仿真结果与试验值最为接近。

3.3 加载方式选取

突变的加载会在模型中产生非真实的应力波，从而激发模型的振动，在准静态分析的加载方式中，应尽量使加载力平滑。在LS－DYNA的关键字中，有两种加载曲线定义方式，分别为斜坡加载和平滑加载，如图5所示，其中上人体模块施加力为13 700N，下人体模块施加力为22 700N。

平滑曲线在整个加载过程中呈S形，其加速度曲线的二阶导数连续，避免了加载初期和末期的加速度突变，也就避免了突然加载和突然卸载造成的冲击振荡。定义＊DEFINE＿CURVE＿SMOOTH中各参数值，就可以非常容易的得到平滑加载曲线。

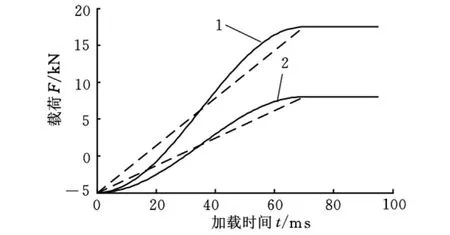
图5 斜坡加载和平滑加载曲线

由斜坡加载和平滑加载得到的节点位移分别为96.7mm和98.4mm。结果表明，两种加载方式对最终参考节点位移的影响不大，但是平滑加载能更快更平稳地达到稳定状态。

3.4 网格局部优化

在某些较窄的焊接翻边区域，往往有较大变形。传统仿真模型没有对这类区域进行特殊处理，翻边只有1～2层网格，意味着此时宽度方向仅有2～3个节点，这将无法准确描述复杂的曲面变形。而且较少的节点也导致接触搜索失效，该区域则会出现失真的穿透和毛刺现象。本文对这些区域网格进行了局部细化，其结果如图6所示。图6是细化前后的仿真结果对比。图6a中，网格变形尖锐，不同部件之间甚至出现了交叉现象，这是非真实的。图6b是经过细化网格后的仿真结果，局部变形更加光顺，也没有出现部件交叉的现象，细化网格后的仿真结果更加真实。

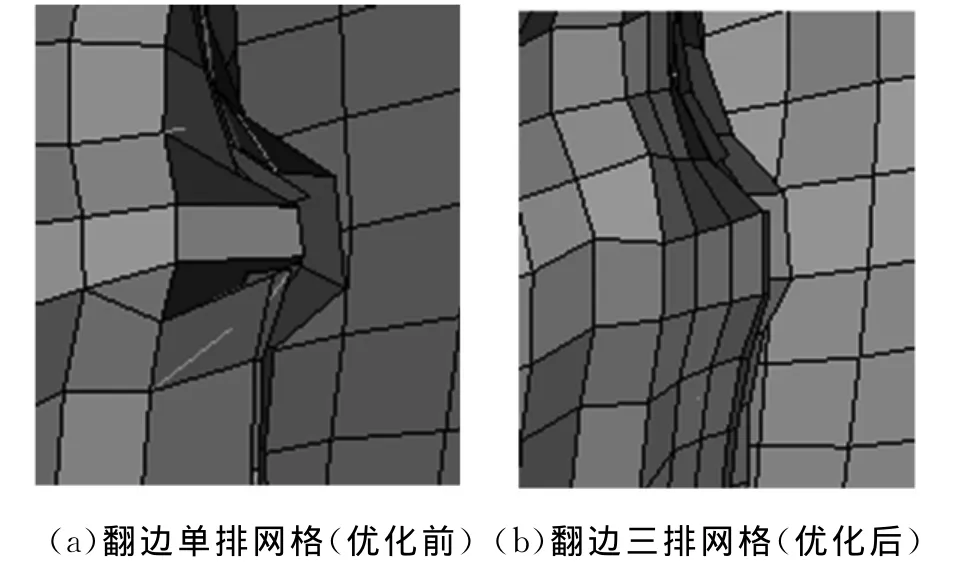
图6 网格局部优化结果对比

3.5 最终结果及验证

将优化的模型与最初模型对比，其结果如表3所示。

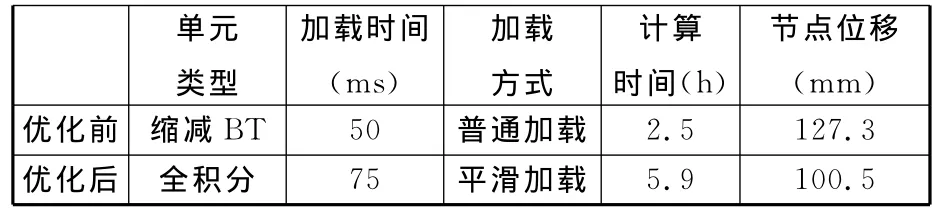
表3 模型优化前后的结果对比

由表3可见，对比模型优化前后的计算结果可见，优化后的局部变形光滑而真实。模型优化前后的仿真结果节点位移改进幅度达21%，实车试验中该节点位移为96.5mm，模型优化后的节点位移误差仅为4.1%。满足工程应用需求。

从图7的仿真与试验对比中也容易看到，优化后结果变形与实车试验变形结果接近度相当高。

图7 实车试验与优化后仿真结果图

这种经过优化的模型已在多款国产微客的座椅安全带仿真中得到使用，表4列出了其中三款车型共7次试验的数据。可以看出，仿真误差基本控制在试验值的5%以内，其精度较高，稳定性较强。

表4 7次试验与仿真结果节点位移表 mm

4 结束语

对于汽车座椅安全带固定点试验的仿真分析，使用基于显式算法的计算模型，能够较方便地模拟真实试验过程。在此基础上，通过改进模型关键参数和局部细节处理方法，使得仿真结果精确度和稳定性大幅提升，计算结果可以准确反映实际试验结果，可靠的用于设计指导和性能评判依据，从而取代成本高、周期长的实车试验过程，成为工程师结构设计的有力工具。

［1］徐中明，郝炜雅.汽车座椅强度及碰撞仿真分析［J］，重庆大学学报，2009，32（5）：512－515.

［2］胡玉梅.汽车正面碰撞设计分析技术及应用研究［D］.重庆大学，2002.

［3］苗强，葛如海，高卫民.车用儿童约束装置建模与仿真分析［J］.上海汽车，2007（4）：20－24.

［4］朱静.大客车顶部结构强度分析及翻滚碰撞性能研究［D］.西安：长安大学，2008.

［5］王青春，范子杰.利用LS－DYNA计算结构准静态压溃的改进算法［J］.力学与实践，2003，25（3）：20－23.

［6］许早龙，范朝兵.基于LS－DYNA的汽车安全带固定点强度研究［J］.力学与实践，2010，32（3）：105－110.

［7］庄茁，ABAQUS/Standard有限元软件入门［M］.北京：清华大学出版社，1998.