数控位置伺服系统控制策略研究

张礼兵 游有鹏 吴 婷

1.南京航空航天大学，南京，210016 2.嘉兴学院，嘉兴，314001

0 引言

数控系统朝向高速高精度发展，是数控机床适应现代先进制造技术发展的必然趋势。高速高精度加工技术对数控机床的数控系统和伺服控制的性能提出了更高的要求。高性能的数控系统和高精度的位置控制策略是提高数控机床加工精度和加工效率的关键要素。高精度的位置伺服控制系统既要有良好的动态响应能力和静态稳定性，又要有很强的抗干扰能力，即鲁棒性［1］。传统位置伺服控制通常采用PID控制方法［2］，但是在数控机床高速加工过程中，位置伺服控制系统是一个多变量、非线性、强耦合的控制对象，基于经典控制理论的控制方法，在参数匹配良好的情况下可以获得较好的性能，一旦系统参数发生变化或者受到内在或外界的干扰，将导致控制性能下降［3］。因此，单纯的PID控制方法，不适合应用于高速高精度数控机床的位置伺服控制系统。为了提高位置伺服控制的性能，文献［4］使用了一种神经网络IP位置控制器，有效地改进了IP控制器的抗干扰性，取得了较好的控制效果；文献［5］结合神经元的自学习能力，设计了一种神经元离散滑模结构的位置伺服控制算法，削弱了常规滑模结构控制中的抖振现象，使得系统性能得到了提高；文献［6］提出一种神经网络与变结构相融合的控制策略并用于非线性机器人控制，提高了系统的鲁棒性。虽然这些方法对系统的性能有了一定的改善，但是这些方法存在控制复杂、计算量大和实时性较差等缺点，因此不能很好地满足高速高精度数控机床位置伺服控制的实时性要求。

近年来，许多研究人员致力于预测控制和模糊逻辑控制的研究，它们已成为智能控制领域的研究热点之一。文献［7］提出了一种多电机多模型动态矩阵预测控制算法，对多电机的同步控制效果较好。文献［8］采用阶跃响应法建立控制对象的数学模型，将预测控制的思想用于位置跟踪系统的控制，所设计的控制器具有较好的跟踪性能和鲁棒性能。文献［9］针对永磁同步电机交流伺服系统，采用模糊控制方法进行控制，与常规PID控制的交流伺服系统相比，具有良好的动态响应能力、稳态性能以及较强的鲁棒性。文献［10］针对永磁直线同步电机伺服系统参数不确定性设计了一种自构式反馈模糊神经网络控制器，结果表明控制系统具有较强的鲁棒性。因此，预测控制和模糊逻辑控制具有良好的控制性能。

本文采用模糊推理和预测控制相结合的控制策略，提出一种基于模糊推理的广义预测控制方法对数控位置伺服控制系统进行控制。采用广义预测控制方法对数控位置伺服控制系统设计位置广义预测控制器，根据实际反馈偏差及其变化率，采用模糊逻辑推理方法进行自适应的调整控制量，从而有效地提高了位置伺服控制系统的动态响应能力、稳态性能和鲁棒性。

1 数控位置伺服控制模型

数控位置伺服控制系统由位置环、速度环和电流环等组成，其结构如图1所示。由于控制对象的结构、参数和环境具有不确定性，往往很难从机理上获得系统的精确的数学模型。为了建立特定应用场合的被控对象的数学模型，需要根据系统的输入和输出数据对控制系统的结构、参数和模型进行辨识，从而获得位置伺服控制系统的模型，模型表达式为

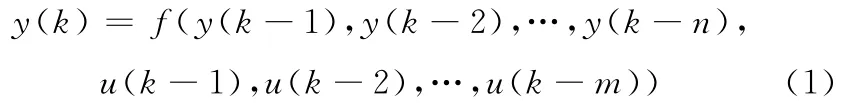
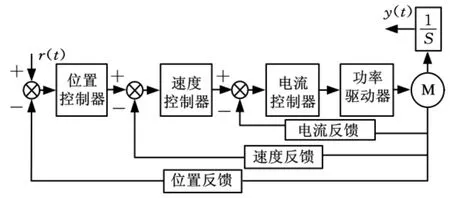
图1 数控位置伺服控制系统框图

式中，u和y分别为系统的输入和输出；n和m分别为系统阶次和输入阶次。

将式（1）进行时间序列离散化处理，可以得到系统的差分方程形式的表达式：

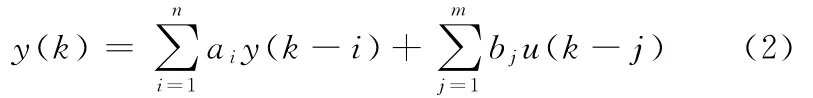
根据文献［11］和［12］中的利用输入和输出数据进行系统模型辨识的思想，本文采用网格搜索算法和递推最小二乘法相结合的思想对控制系统的模型结构和模型参数进行辨识，从而可以获取数控位置伺服控制系统的数学模型。

1.1 模型结构辨识

模型结构辨识主要是确定系统的系统阶次n和输入阶次m。采用网格搜索算法对控制系统的模型结构辨识就是将系统阶次n和输入阶次m分别取N个值和M个值，对N×M个（n，m）的组合利用递推最小二乘法的方法进行寻优求解，使目标函数值最小。以施耐德400W十字平台中的一个轴作为被控对象进行结构辨识，以辨识建立的数学模型表达式和输出数据的均方误差mse为目标函数，其表达式以及系统满足的条件如下：

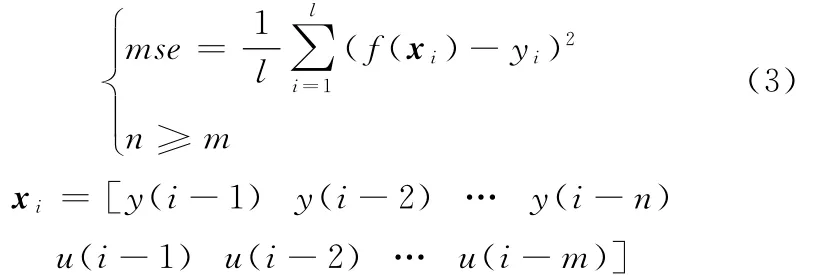
式中，f（xi）为辨识建立的数学模型；yi为采集的输出数据。

在MATLAB软件平台下导入输入和输出数据，并经过模型结构辨识算法得到的辨识结果为

1.2 模型参数辨识

经过模型结构辨识后，模型的表达式可以表示为

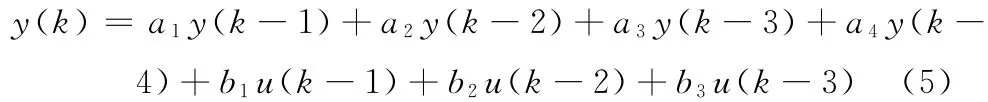
模型参数辨识就是确定式（5）中的未知量a1～a4和b1～b3的实际值。采用递推最小二乘法进行模型参数辨识，其基本思想为：新的估计值等于旧的估计值与修正值之和。递推最小二乘法的递推公式为［13］

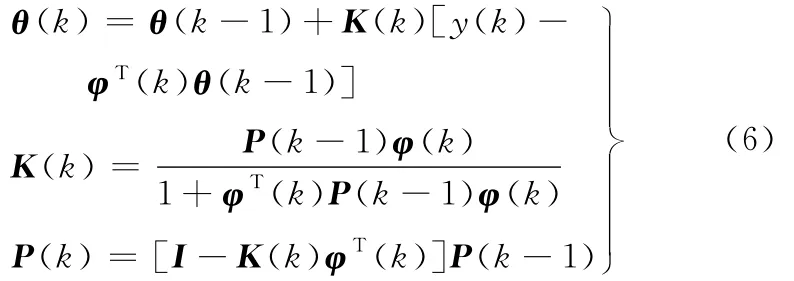
其中，φ（k）＝ ［y（k－1）y（k－2）y（k－3）y（k－4）u（k－1）u（k－2）u（k－3）］，θ（k）＝［a1a2a3a4b1b2b3］，当k＝0时，P（0）＝106I，θ（0）＝0，I为单位矩阵。

在MATLAB软件平台下导入输入和输出数据，采用递推最小二乘法算法得到模型参数辨识结果为

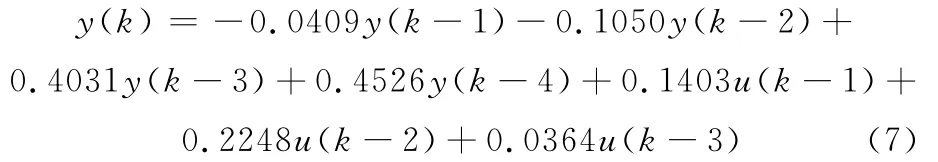
2 位置伺服控制策略

式（7）是一个理想模型，实际的位置伺服控制系统在运行过程中，由于受到干扰等因素的影响，系统具有不确定性，因此该模型不能很好地反映数控位置伺服控制系统的实际模型。实际的模型可以采用CARIMA模型来描述：

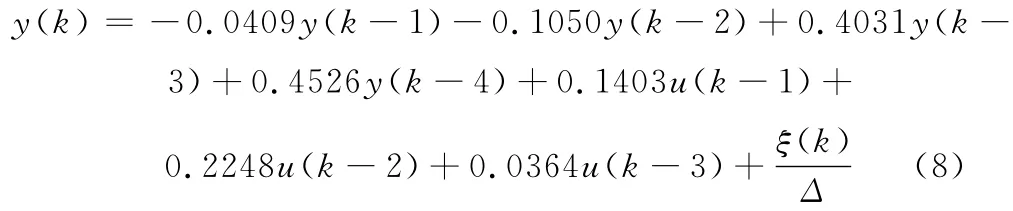
式中，ξ（k）为系统的白噪声；Δ为差分算子，Δ＝1－z－1。

2.1 模糊推理广义预测控制

式（8）实际上是一个线性模型，但位置伺服控制系统一般为复杂的非线性动态系统，采用线性模型作为预测模型，必然存在模型误差，当采用传统的广义预测控制策略时，如果模型严重失配可能破坏系统的稳定性。因此，在进行数控位置伺服控制时，为了有效地改善控制器的抗干扰能力和提高控制效果，采用基于模糊逻辑推理的广义预测控制策略，其中式（8）作为广义预测控制的预测模型，通过滚动优化计算系统的最优控制率，控制预测模型的输出；对模型失配或者其他干扰因素引起的输出偏差通过模糊逻辑推理在线反馈校正，进行非线性误差补偿，从而克服了传统的广义预测控制方法的缺点。其控制结构框如图2所示。

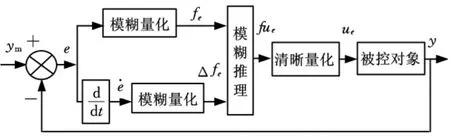
图2 模糊推理广义预测控制原理框图

2.2 广义预测控制

将式（8）进行变形，得到一般形式的表达式：

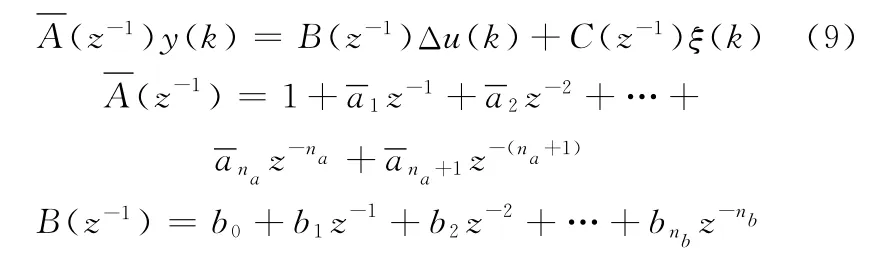
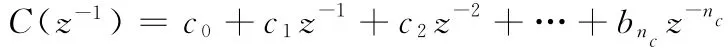
根据预测理论，为了预测前j步输出，引入Diophantine方程：

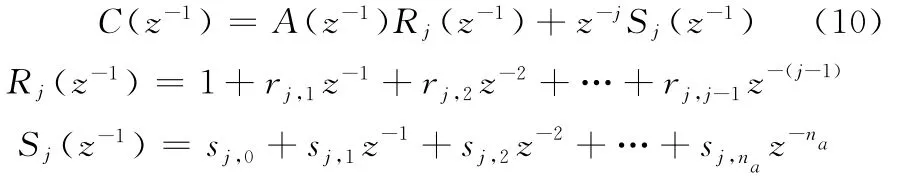
当C（z－1）＝1时，对式（9）和式（10）联立求解，可以求出前j步模型预测输出：

式中，Y、ΔU、ΔU（R－1）分别为未来的预测输出、当前和未来的控制增量、过去的控制增量。

采用对输出误差和控制增量加权的二次型性能指标作为控制条件，其性能指标可以表示为

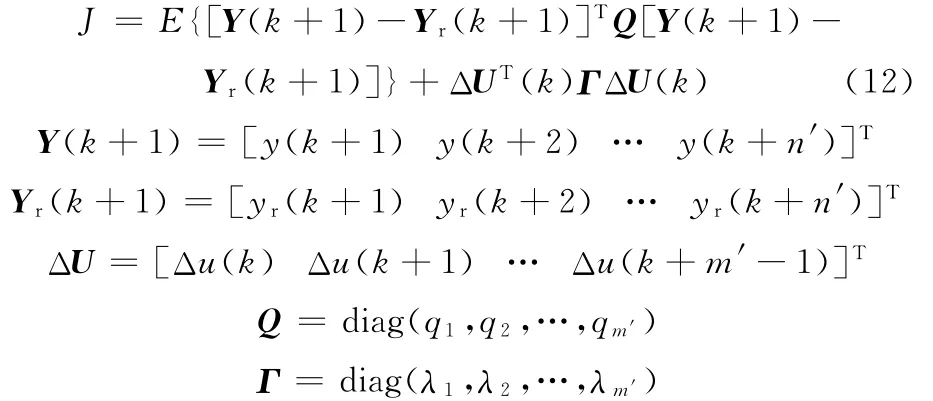
式中，n′为预测时域；m′为控制时域。

根据式（11）和式（12）可以计算出j步模型预测性能最佳的控制增量。

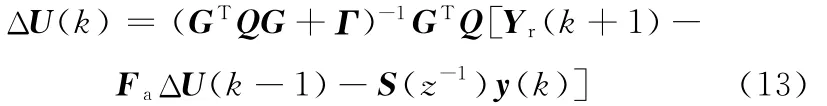
2.3 反馈误差的模糊推理

由于实际系统多为复杂的非线性系统，采用CARIMA模型进行建模存在建模误差，或者系统受到其他干扰等不确定性因素的影响，系统必然存在输出偏差。设k时刻数控位置实际输出为

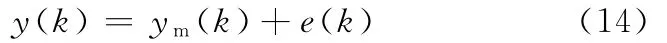
式中，ym（k）为k时刻的预测模型输出；e（k）为k时刻位置伺服系统实际位置与预测模型输出位置的偏差。

假定在输入控制量u（k）的作用下，k＋1时刻通过周期采样得到实际输出位置为y（k＋1），模型预测输出位置为ym（k＋1），定义实际位置输出与预测输出偏差和偏差变化率分别为

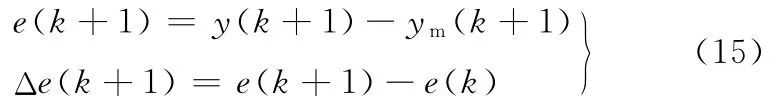
采用二维模糊控制对位置反馈偏差进行实时在线校正，模糊控制器以偏差fe和偏差变化率Δfe为输入变量，以偏差的控制量fue为输出量。模糊量的隶属函数采用等腰三角形。模糊控制规则可以表示为

iffe是AiandΔfe是Bi，则fue是Ci

其 中，Ai，Bi，Ci∈ ｛NB，NM，NS，ZE，PS，PM，PB｝＝｛负大，负中，负小，零，正小，正中，正大｝，i＝1，2，…，49。

清晰化计算采用加权平均法，表达式如下：

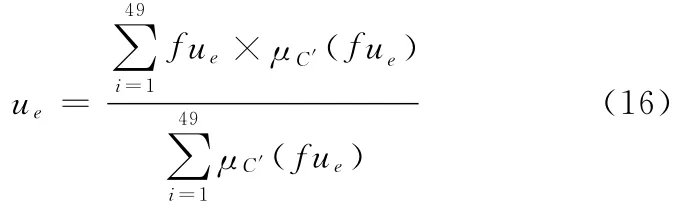
在线反馈校正的模糊逻辑推理过程如图3所示。

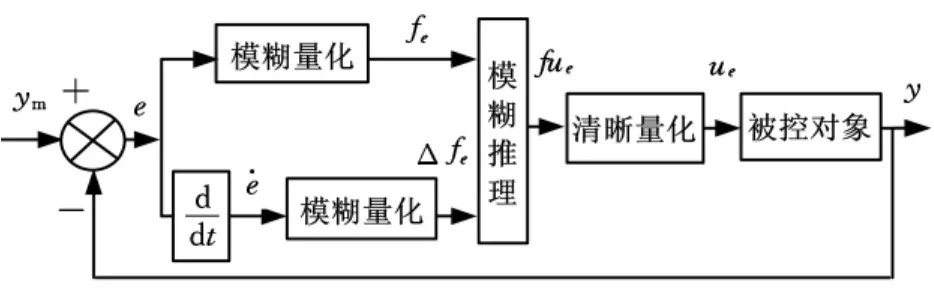
图3 反馈校正的模糊推控制图

3 仿真与实验验证

3.1 仿真验证

为了验证基于模糊推理的广义预测控制的控制效果，在MATLAB软件环境下对该方法通过算法编程进行仿真模拟验证。

数控位置伺服控制系统的数学模型如式（8）所示，设仿真所采用到的控制参数，即预测时域n′＝3，控制时域m′＝2，控制加权系数Γ＝diag（0.01，0.01，…，0.01），输出柔化系数α＝0.01，预测模型的白噪声ξ（k）取值范围为［－0.3，＋0.3］mm。期望输出指令cmd＝100mm，在白噪声的干扰下其仿真结果如图4所示。

3.2 实验验证

为了进一步验证本文所提出的控制算法的有效性，在施耐德400W十字平台上进行了基于模糊推理广义预测控制方法和传统的PID控制方法的对比实验，实验条件如表1所示。

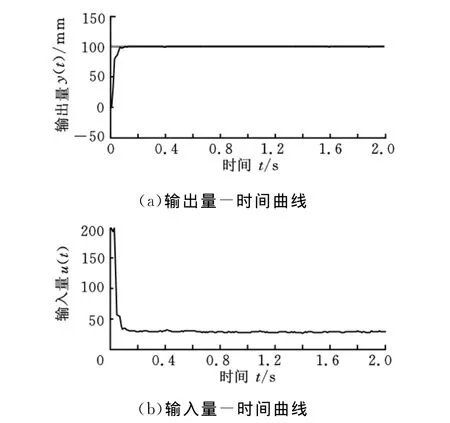
图4 基于模糊推理的广义预测控制输入和输出信号图

表1 实验条件表

以十字平台中的其中的一个轴为被控对象，采样周期Ts＝2ms，控制时间长度t＝2000ms，分别采用模糊推理的广义预测控制方法和传统的PID控制方法进行实验。设期望输出指令cmd＝100mm，通过调试，广义预测控制算法中，预测时域n′＝3，控制时域m′＝2，控制加权系数Γ＝diag（0.8，0.8，…，0.8），输出柔化系数α＝0.78，输出的阶跃结果如图5a所示。通过调试，设置PID控制参数为kp＝0.013，ki＝0，kd＝0.02，其输出的阶跃结果如图5b所示。在PID控制调试过程中，当参数取值增大时，发生超调严重。

图5 cmd＝100mm时两种控制方法的输出结果图

设 输 入 为 （ 0，30 000 ），（30 000，48 000），（48 000，60 000）（单 位：脉 冲数）三段直线指令，输出结果如图6所示，其中虚线为输入指令，实线为输出数据。

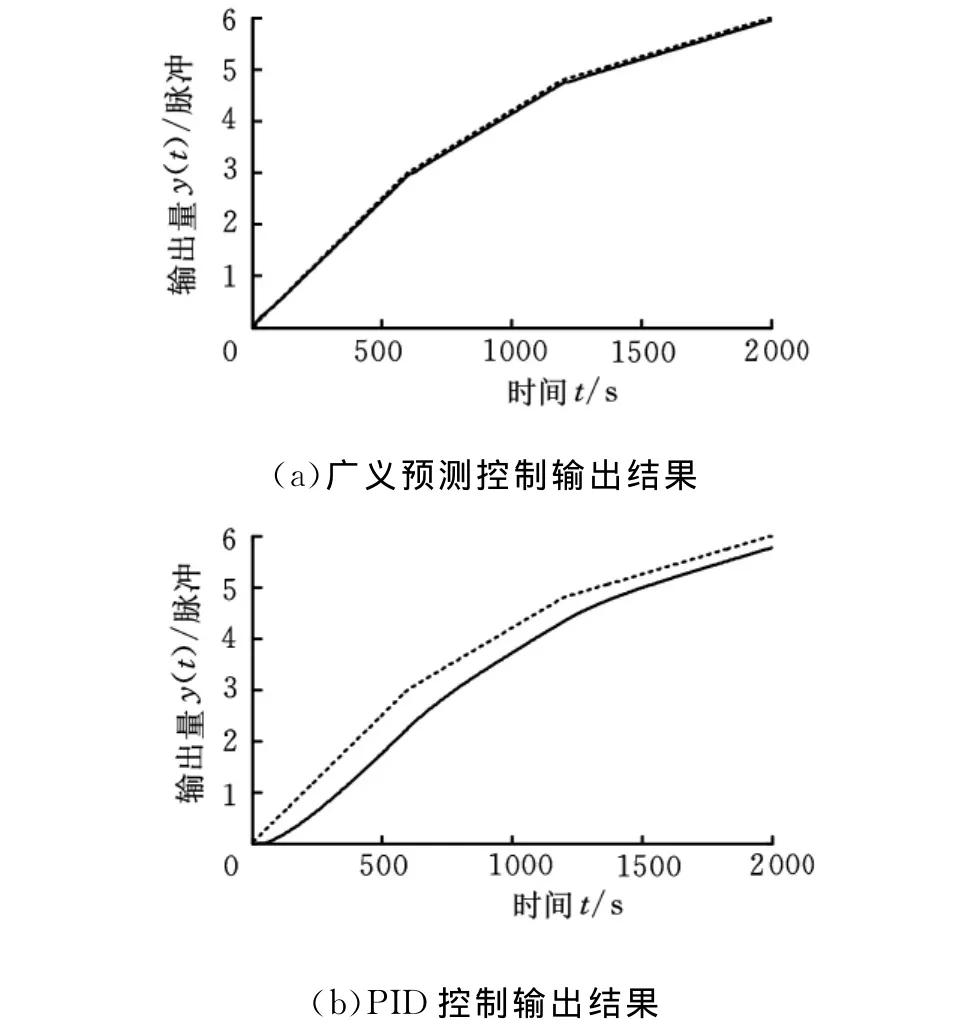
图6 三条线段的两种控制方法的输出结果图

通过分析仿真实验，期望输出指令为cmd＝100mm时，当系统达到稳定状态后，从图4中可以看出，在［－0.3，0.3］mm范围的白噪声的干扰下，输入信号在平衡位置附近微小波动，调整输入信号量，使输出结果基本上稳定在100mm附近。因此，基于模糊推理的广义预测控制方法具有较强的稳态性能和鲁棒性。

通过十字平台的期望输出指令cmd＝100mm的阶跃实验，通过图5可以得出，广义预测控制的上升时间比PID控制的上升时间小了很多，响应速度特别快。因此，广义预测控制具有更好的动态性能。通过三段直线的控制实验，根据实验结果（图6），广义预测控制的跟踪误差比PID控制的跟踪误差更小，跟踪性能更好。因此，基于模糊推理的广义预测控制方法用于数控位置伺服控制系统中，能够提高系统的动态性能和跟踪性能。

4 结语

在深入分析高速高精度加工技术对数控位置伺服控制提出的更高要求的基础上，提出了一种基于模糊逻辑推理的广义预测控制方法，详细地阐述了该方法实现原理和控制过程。通过MATLAB仿真和施耐德十字平台实验，与传统的PID控制方法的对比分析与应用实验表明，该方法具有很好的动态性能、稳态性能和鲁棒性，更适合应用于高速高精度数控系统的位置伺服控制系统。

［1］陈幼平，张代林，艾武，等.基于DSP的直线电机位置伺服控制策略研究［J］.电机与控制学报，2006，10（1）：61－65.

［2］Comins P，Munro N.PID Control：Recent Tuning Methods and Design to Specification［J］.IEEE Proceeding：Control Theory Application，2002，149（1）：46－53.

［3］许强，贾正春，熊有伦.交流伺服系统最优位置控制［J］.微电机，2000，33（2）：18－20.

［4］王军，肖建.永磁同步电动机自适应神经网络IP位置控制器［J］.电机与控制学报，2005，9（6）：525－528.

［5］史晓娟.一种基于神经元离散滑模变结构的位置控制方法［J］.仪器仪表学报，2008，29（7）：1559－1562.

［6］张文辉，齐乃明，尹洪亮.自适应神经变结构的机器人轨迹跟踪控制［J］.控制与决策，2011，26（4）：597－600.

［7］张今朝，刘国海，潘天红.多电机变频调速同步系统的多模型预测控制［J］.控制与决策，2009，24（10）：1489－1494.

［8］苏义鑫，周祖德，陈幼平，等.位置跟踪系统的预测控制研究［J］.中国机械工程，2001，12（12）：1356－1359.

［9］葛锁良，刘文慰.基于模糊控制的交流伺服系统的设计［J］.东南大学学报，2003，33（9）：154－157.

［10］王丽梅，武志涛，左涛.永磁直线电机自构式模糊神经网络控制器设计［J］.电机与控制学报，2009，13（5）：643－647.

［11］Erkorkmaz K，Wong W.Rapid Identification Technique for Virtual CNC Drives［J］.International Journal of Machine Tools ＆ Manufacture，2007，47：1381－1392.

［12］Wong W，Erkorkmaz K.Constrained Identification of Virtual CNC Drives using a Genetic Algorithm［J］.International Journal Advanced Manufacturing Technology，2010，50：275－288.

［13］李国勇.智能预测控制及其MATLAB实现［M］.北京：电子工业出版社，2009.